Вопрос 2. Основное уравнение гидростатики

Основное уравнение гидростатики получают из дифференци­альных уравнений равновесия жидкости. Рассмотрим равновесие жидкости, находящейся в относительном покое. В этом случае на нее действуют массовые силы — силы тяжести и инерции — и по­верхностные — сила гидростатического давления. Выделим из всего объема жидкости элементарный бесконечно малый паралле­лепипед объемом dV.

Ребра параллелепипеда dx, dy, dz расположены параллельно осям х, у, z, как показано на рис. 3.1.Средняя сила гидростатичес­кого давления, действующая на каждую грань со стороны окружа­ющей жидкости, равна произведению гидростатического давления на площадь грани параллелепипеда. Согласно рис. 3.1. р=f{x, у, z). Определим вид этой функциональной зависимости. Для этого со­ставим суммы проекций на оси х, у, z всех сил, действующих на элементарный параллелепипед. Обозначим проекции на оси х, у, z всех массовых сил, отнесенных к единице массы, через X, Y, Z. Проекция объемных сил, например, на ось х будет равна dQ = Xdm, где масса жидкости dm = ρdxdydz, или dQ = Xρdxdydz. Согласно основному закону статики сумма проекций всех сил, действующих на жидкость, в случае покоя равна нулю.

Рис 1. К выводу дифференциальных уравнений равновесия Эйлера для гидростатики

Систематизируем полученные уравнения:

Эта система дифференциальных уравнений, полученная Л. Эйлером, описывает условия равновесия элементарного параллелепипеда жидкости. Умножим каждое из уравнений (3.2.) соответственно на dx, dy и dz и сложим полученную систему уравнений:

Поскольку гидростатическое давление является функцией только координат, левая часть уравнения представляет собой полный дифференциал давления

Правая часть равнения также представляет собой полный дифференциал некоей силовой функции, так как плотность постоянна.

В случае абсолютного покоя жидкости отсутствуют инерционные силы и сила тяжести будет направлена вертикально вниз, т.е. Ζ = - g; X=0; Y=0. Тогда

dp=-ρgdz. (3.4.)

Разделив правую и левую части этого уравнения на ρg, представим уравнение (3.4.) в виде

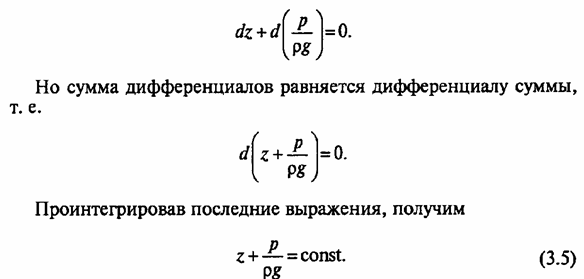
Для двух частиц жидкости m₀ и m₁, находящихся на высотах z₁ от произвольно выбранной плоскости отсчета, уравнение (3.5.) можно записать в следующем виде:

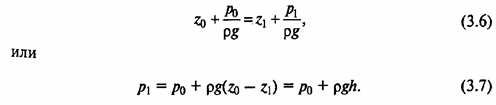
Последнее выражение называется законом Паскаля, который гласит, что давление в любой точке несжимаемой жидкости, передается одинаково всем точкам объема жидкости.

Уравнение (3.5) и вытекающие из него уравнения (3.6) и (3.7) яв­ляются основными уравнениями гидростатики.

В уравнении (3.6) величина p/(pg) называется статическим или пьезо­метрическим напором, a z — ниве­лирной высотой. Обе эти величи­ны выражаются в единицах длины (м). Основной закон гидростатики можно сформулировать так: для каждой точки жидкости, находя­щейся в покое, сумма нивелирной вы­соты и статического напора — ве­личина постоянная.

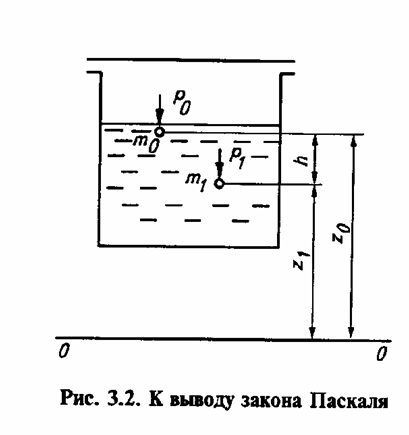
Статический напор характеризует удельную потенциальную энергию давления в данной точке, а нивелирная высота — удель­ную потенциальную энергию положения данной точки над плос­костью сравнения, т. е. энергию, приходящуюся на единицу веса жидкости .

Таким образом, основное уравнение гидростатики (3.5) являет­ся частным случаем закона сохранения энергии: удельная потенци­альная энергия во всех точках жидкости, находящейся в покое, — ве­личина постоянная.

Из уравнения (3.3) легко получить уравнение поверхности уровня или поверхности равного давления. Такой поверхностью называют в гидравлике поверхность, все точки которой испытыва­ют одинаковое давление, т. е. dp = 0 и Xdx + Ydy + Zdz = 0.

Для случая абсолютного покоя последнее уравнение примет вид

-gdz=0

или

dz=0

z=const.

Таким образом, при абсолютном покое поверхность уровня представляет собой горизонтальную поверхность.

Дата добавления: 2014-01-03