Свободные механические колебания (незатухающие и затухающие)

Механические колебания и волны.

Лекция 3.

Механические колебания: гармонические, затухающие, вынужден­ные. Резонанс. Автоколебания. Энергия гармонических колебаний. Раз­ложение колебаний в гармонический спектр. Применение гармонического анализа для обработки диагностических данных. Механические волны, их виды и скорость распространения. Уравнение волны. Энергетические ха­рактеристики волны. Эффект Доплера и его применение для неинвазивно­го измерения скорости кровотока.

Повторяющиеся движения или изменения состояния называют колебаниями (переменный электрический ток, движение маятника, работа сердца и т. п.). Всем колебаниям, независимо от их природы, присущи некоторые общие закономерности. В зависимости от характера взаимодействия колеблющейся системы с окружающими телами различают колебания свободные, вынужденные и автоколебания. Колебания распространяются в среде в виде волн. В данной главе рассматриваются механические колебания и волны.

Свободными (собственными) колебаниями называют такие, которые совершаются без внешних воздействий за счет первоначально полученной телом энергии. Характерными моделями таких механических колебаний являются материальная точка на пружине (пружинный маятник) и материальная точка на нерастяжимой нити (математический маятник).

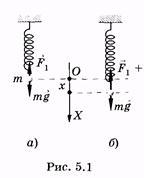
В этих примерах колебания возникают либо за счет первоначальной потенциальной энергии (отклонение материальной точки от положения равновесия и движение без начальной скорости), либо за счет кинетической (телу сообщается скорость в начальном положении равновесия), либо за счет и той и другой энергии (сообщение скорости телу, отклоненному от положения равновесия). Рассмотрим пружинный маятник. В положении равновесия (рис. 5.1, а) упругая сила 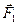уравновешивает силу тяжести 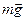. Если оттянуть пружину на расстояние х (рис. 5.1, б), то на материальную точку будет действовать большая упругая сила. Изменение значения упругой силы (F), согласно закону Гука, пропорционально изменению длины пружины или смещению х точки:

F = -kx, (5.1)

где k — коэффициент пропорциональности между силой и смещением, который в данном случае является жесткостью пружины; знак минус показывает, что сила всегда направлена в сторону положения равновесия: F < 0 при х > 0, F > 0 при х < 0.

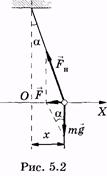
Другой пример. Математический маятник (рис. 5.2) отклонен от положения равновесия на такой небольшой угол а, чтобы можно было считать траекторию движения материальной точки прямой линией, совпадающей с осью ОХ. При этом выполняется приближенное равенство:

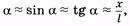(5.2)

где х — смещение материальной точки относительно положения равновесия, l — длина нити маятника.

На материальную точку (рис. 5.2) действуют сила натяжения нити 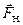сила тяжести 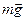, модуль их равнодействующей равен

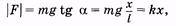(5.3)

где k — коэффициент пропорциональности между силой и смеще­нием, который в данном случае равен

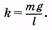(5.4)

Сравнивая (5.3) и (5.1), видим, что в этом примере равнодейст­вующая сила подобна упругой, так как пропорциональна смеще­нию материальной точки и направлена к положению равновесия. Такие силы, неупругие по природе, но аналогичные по свойствам силам, возникающим при малых деформациях упругих тел, на­зывают квазиупругими.

На материальные точки, рассмотренные в этих примерах, кро­ме упругой и квазиупругой силы действует и сила сопротивления (трения), модуль которой обозначим F_c (на рисунках не показана).

Дифференциальное уравнение, описывающее движение мате­риальной точки, получаем на основании второго закона Ньютона (произведение массы тела на его ускорение равно сумме всех дей­ствующих сил):

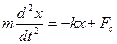(5.5)

Выражение для смещения материальной точки, которое полу­чается из решения этого уравнения, рассмотрим для некоторых частных случаев.

Незатухающие колебания. Рассмотрим модель, в которой пренебрегают силой сопротивления (F_c = 0). Из (5.5) имеем: 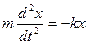. Заменяя

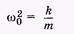(5.6)

и преобразуя, получаем следующее дифференциальное уравнение второго порядка:

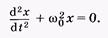(5.7)

Его решение, в чем можно убедиться подстановкой, приводит к гармоническому колебанию:

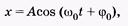(5.8)

где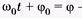— фаза колебаний, j₀ — начальная фаза (при t = 0),

w₀ — круговая частота колебаний, А — их амплитуда.

Амплитуда и начальная фаза колебаний определяются началь­ными условиями движения, т. е. положением и скоростью мате­риальной точки в момент t = 0.

Среди различных видов колебаний гармоническое колебание является наиболее простой формой.

Таким образом, материальная точка, подвешенная на пружине (пружинный маятник) или нити (математический маятник), со­вершает гармонические колебания, если не учитывать силы со­противления.

При преобразовании дифференциального уравнения гармониче­ского колебания величина 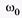была введена формально [см. (5.6)], однако она имеет важный физический смысл, так как определяет частоту колебаний 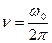системы и показывает, от каких факторов (параметров) эта частота зависит: от жесткости пружины и массы в одном примере, длины нити и ускорения свободного паде­ния в другом.

Период колебаний может быть найден из формулы

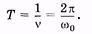(5.9)

Используя (5.6), получаем период колебаний пружинного ма­ятника

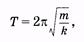(5.10)

подставляя вместо k выражение (5.4), находим период колебаний математического маятника

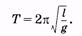(5.11)

Очень удобно изображать гармонические колебания с по­мощью векторных диаграмм. Этот метод состоит в следующем. Из начала оси абсцисс проведем вектор 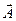(рис.5.3), проекция которо­го на ось ОХ равна Acos j. Если вектор 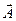будет равномерно вращать­ся с угловой скоростью w₀ против часовой стрелки, то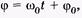где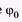— начальное значение j, и проекция вектора 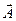на ось ОХ бу­дет изменяться со временем по закону (5.8). В таком представлении амплитуда колебаний есть модуль равномерно вращающегося векто­ра 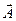, фаза колебаний — угол между вектором 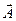и осью ОХ, началь­ная фаза — начальное значение этого угла, круговая частота колеба­ний — угловая скорость вращения вектора, 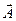смещение х колеблю­щейся точки — проекция вектора 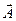на ось ОХ.

Чтобы найти скорость материальной точки при гармоничес­ком колебании, нужно взять производную от выражения (5.8) по времени:

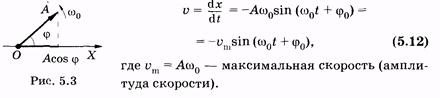
На основании тригонометрических формул преобразуем (5.12):

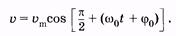(5.13)

Сравнивая (5.13) и (5.8), замечаем, что фаза скорости на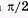больше фазы смещения, т. е. скорость опережает по фазе смеще­ние на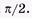

Продифференцировав (5.12), найдем ускорение:

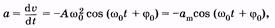(5.14)

где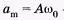— максимальное ускорение (амплитуда ускорения).

Вместо (5.14) запишем

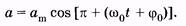(5.15)

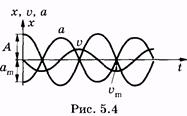
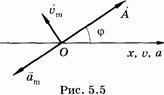
Из сравнения (5.15) и (5.8) следует, что фазы ускорения и сме­щения различаются на л, т. е. эти величины изменяются в противофазе. Графики зависимости смещения, скорости и ускорения от времени показаны на рис. 5.4, а их векторные диаграммы — на рис. 5.5.

Затухающие колебания. В реальном случае на колеблющее­ся тело действуют силы сопротивления (трения), характер движе­ния изменяется, и колебание становится затухающим. Для того чтобы из уравнения (5.5) найти временную зависимость затухаю­щего колебания, необходимо знать, от каких параметров и как за­висит сила сопротивления. Обычно предполагают, что при не очень больших амплитудах и частотах эта сила пропорциональна скорости движения и, естественно, направлена противоположно скорости: 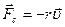, где r — коэффициент трения (сопротивления), характеризующий свойства среды оказывать сопротивление.

Применительно к одномерному движению последней формуле придадим следующий вид:

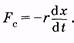(5.16)

Подставим выражение (5.16) в уравнение (5.5) и получим:

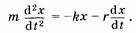(5.17)

Разделив обе части уравнения на т, запишем его в стандарт­ной форме:

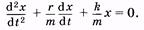(5.18)

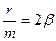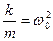После замены и получаем окончательную запись дифференциального уравнения свободных колебаний с учетом сил сопротивления:

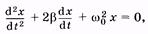(5.19)

где b - коэффициент затухания, w₀ – круговая частота собственных колебаний системы (без затухания).

Решение (5.19) существенно зависит от знака разности 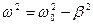, где w - круговая частота затухающих колебаний. При w² - b² > 0 круговая частота w является действительной величиной и решение уравнения (5.19) будет следующим:

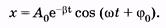(5.20)

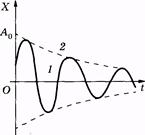
График этой функции показан на рис. 5.6 сплошной кривой 1; штриховой линией 2 изображено изменение амплитуды:

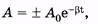(5.21)

где значение А ₀ приведено на рисунке.

Период затухающих колебаний зависит от коэффициента тре­ния и определяется формулой:

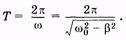(5.22)

При очень малом трениипериод затухающего колебания близок к периоду незатухающего свободного колебания: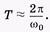

Быстрота убывания амплитуды колебаний определяется коэф­фициентом затухания: чем сильнее тормозящее действие среды, тем больше b и тем быстрее уменьшается амплитуда. На практи­ке, однако, степень затухания часто характеризуют логарифми­ческим декрементом затухания, понимая под этим величину, равную натуральному логарифму отношения двух последовательных амплитуд, разделенных интервалом времени, равным пери­оду колебаний:

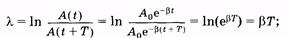
следовательно, коэффициент затухания и логарифмический дек­ремент затухания связаны достаточно простой зависимостью:

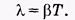(5.23)

Рис. 5.6 Рис. 5.7

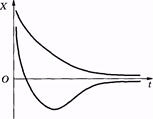
При сильном затухании (b² > w²) из формулы (5.22) видно, что период колебания является мнимой величиной. Движение в этом случае уже не будет периодическим и называется апериодическим*.

Возможные апериодические движения представлены в виде графиков на рис. 5.7. Этот случай применительно к электриче­ским явлениям рассматривается в гл. 14.

* Заметим, что если некоторая физическая величина принимает мни­мые значения, то это означает какую-то необычность, экстраординар­ность соответствующего явления. В рассмотренном примере экстраорди­нарность заключается в том, что процесс перестает быть периодическим.

Дата добавления: 2014-01-03