Будущая стоимость аннуитета

Аннуитет — это поток равных сумм денежных средств, возникающий через равные промежутки времени. Сумма в 1000 долл., получаемая в конце каждого года ежегодно в течение 10 лет, — пример аннуитета. Потоки денежной наличности могут быть притоками дохода, полученными от инвестирования, или оттоками средств, инвестируемых с целью получения будущих доходов. Инвесторов иногда интересует определение будущей стоимости аннуитета. Как правило, это касается так называемого обычного аннуитета — того, при котором регулярное движение денежных средств происходит в конце каждого года.

Будущая стоимость может быть определена математически с использованием калькулятора, компьютера или соответствующих финансовых таблиц. Здесь мы используем таблицы факторов наращения, или факторов будущей стоимости, для аннуитета. Таблица факторов наращения для аннуитета приведена в табл. 5.7 в тексте. Факторы наращения в данной таблице представляют собой сумму, до которой регулярные взносы в 1 долл., сделанные в конце года, выросли бы при различной комбинации периодов и ставок процента.

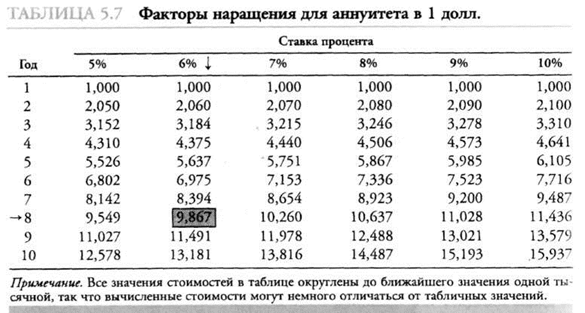
Например, доллар, внесенный на банковский депозит, по которому начисляется 6% в конце каждого года, на период в 8 лет, вырос бы до 9,897 долл. Используя фактор наращения для 8-летнего аннуитета при ставке 6%, можно найти будущую стоимость потока денежных средств, умножив ежегодные вложения средств на соответствующий фактор наращения. В случае инвестирования 1000 долл. в конце каждого года в течение 8 лет под 6% итоговая будущая стоимость составит 9897 долл. (9,897 х 1000).

4. Приведенная стоимость: развитие концепции будущей стоимости

Приведенная стоимость — оборотная сторона будущей стоимости. Приведенная стоимость вместо измерения стоимости текущей суммы в какой-то момент в будущем позволяет определить, сколько будущая сумма денег стоит сегодня. Используя технику приведенной стоимости, можно подсчитать сегодняшнюю стоимость той суммы, которая будет получена в будущее При определении приведенной стоимости будущей суммы денег основным вопросом является такой: сколько денег следовало бы поместить с егодня на счет, по которому выплачивается п процентов, чтобы приравнять их к некой сумме, которая будет получена в будущем? Применяемая при нахождении приведенной стоимости ставка процента обычно называется ставкой дисконта (или альтернативными издержками). Она представляет собой ежегодную ставку доходности, которую можно было бы получить теперь от аналогичного инвестирования. Основные вычисления приведенной стоимости лучше всего иллюстрируются простым примером. Представьте, что у вас появилась возможность получить 1000 долл. ровно через год начиная с сегодняшнего дня. Если бы вы могли получить 8% на аналогичные типы инвестиций, какую наибольшую возможную сумму денег вы заплатили бы за эту возможность?

Другими словами, какова приведенная стоимость 1000 долл., которые должны быть получены через год, дисконтированных по ставке 8%? Пусть X — приведенная стоимость. Чтобы описать этот случай, используется следующее

равенство: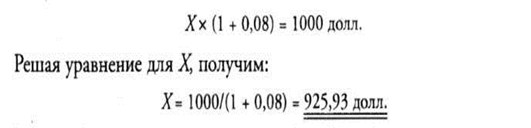

Из этих вычислений должно быть ясно, что приведенная стоимость 1000 долл., которые будут получены через год и дисконтированы по ставке 8%, составляет 925,93 долл. Другими словами, 925,93 долл., размещенные на счете, по которому выплачивается 8%, возрастут до 1000 долл. в течение года. Чтобы проверить это заключение, умножим фактор наращения будущей стоимости для 8% и одного года, или 1,08 (см. табл. 5.6), на 925,93 долл. Эта сумма принесет будущую стоимость в 1000 долл. (1,08 х 925,93).

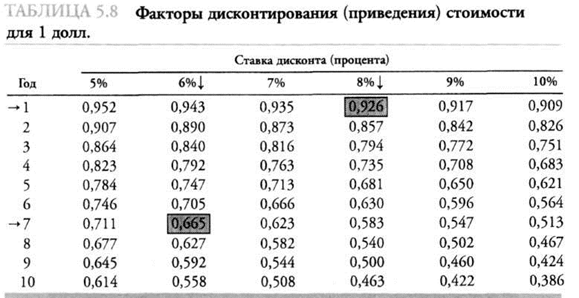
Поскольку вычисления приведенной стоимости сумм, которые будут получены в отдаленном будущем, более сложны, чем для вложений на год, в этом случае рекомендуется использовать таблицы приведенной стоимости (в качестве иллюстрации в табл. 5.8 в тексте приведена их часть). Факторы дисконтирования в таких таблицах представляют собой приведенную стоимость 1 долл., рассчитанную для различных комбинаций периодов и ставок дисконтирования. Например, приведенная стоимость 1 долл., который предполагается получить через год и дисконтированный по ставке 8%, составляет 0,926 долл. На основе этого фактора (0,926) приведенная стоимость 1000 долл., которую предполагается получить через год при ставке 8% дисконта, может быть найдена умножением этого фактора на 1000 долл. Результирующая приведенная стоимость в 926 долл. (0,926 х 1000) соответствует (за исключением небольшой разницы в результате округления) стоимости, подсчитанной ранее.

Другой пример поможет понять, как используются таблицы приведенной стоимости. Приведенная стоимость 500 долл., которые предполагается получить через 7 лет, дисконтированных по ставке 6%, может быть подсчитана следующим образом:

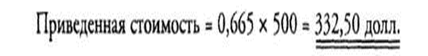
Число 0,665 представляет собой фактор дисконтирования или приведения стоимости для 7 периодов и ставки дисконта в 6%.

Каждый инвестор должен знать некоторые моменты, связанные с таблицами приведенной стоимости. Во-первых, фактор дисконтирования однократной суммы всегда меньше 1; и только если ставка дисконтирования равна нулю, этот фактор равняется 1. Во-вторых, чем выше ставка дисконтироания для данного года, тем меньше фактор дисконтирования. Другими словами, чем выше альтернативные издержки, тем меньше нужно инвестировать сегодня, чтобы получить данную сумму в будущем. Наконец, чем позднее инвестор собирается получить сумму в будущем, тем меньше она стоит сегодня. Важно также отметить, что при ставке дисконтирования 0% фактор дисконтирования всегда равен 1 и, следовательно, в таком случае будущая стоимость некоторой суммы денег равняется ее приведенной стоимости.

Дата добавления: 2014-01-03