Временная форма представления сигнала

Времнным представлением сигнала называется такое разложение сигнала U(t), при котором в качестве базисных функцийиспользуются единичные импульсные функции -дельта-функции:

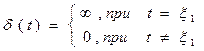
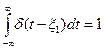
Дельта-функция δ(t) или функция Дирака, представляет собой бесконечно уз­кий импульс с бесконечной амплитудой, расположенный при нулевом значении аргумента функции. «Площадь» импульса тем не менее равна единице. Символическое расположение дельта-функции показано на рис.5.

d(t- x₁) ­ :

½ :

½ ½

½ ½

½ ½ t

0 x

Рис.5

Единственным параметром правильно выражающим реальный сигнал, является время его действия. С помощью d- функции значение реального сигнала можно выразить как:

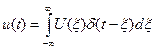(5.5)

Функция u(t) выражена в виде совокупности примыкающих друг к другу импульсов бесконечно малой длительности. Разложение (5) имеет большое значение в теории линейных систем, т.к. установив реакцию системы на элементарный входной сигнал в виде дельта-функции, можно определить реакцию системы на произвольный входной сигнал как суперпозицию реакций на бесконечную последовательность смещенных дельта-импульсов с «площадями», равными соответствующимзначениям входного сигнала. Разумеется, сигнал в виде дельта-функции невозможно реализовать физически, однако эта функция очень важна для теоретического анализа сигналов и систем. На графиках дельта-функция обычно изображается жирной стрелкой, высота ко­торой пропорциональна множителю, стоящему перед дельта-функцией (рис. 1). Одно из важных свойств дельта-функции - так называемое фильтрующее свойство . Оно состоит в том, что если дельта-функция присутствует под интегралом в качестве множителя, то результат интегрирования будет равен значению осталь­ного подынтегрального выражения в той точке, где сосредоточен дельта -импульс:

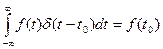Рис 6. График дельта-функции

Функция единичного скачка σ(t) , она же функция Хевисайда, она же функция вклю­чения, равна нулю для отрицательных значений аргумента и единице -для по­ложительных. При нулевом значении аргумента функцию считают либо неопре­деленной, либо равной 1/2:

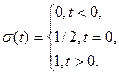
Данную функцию можно смоделировать с помощью оператора срав­нения, возвращающего значение 0 или 1:

Отличие такой реализации функции включения состоит толь­ко в том, что при нулевом значении аргумента результат равен единице; впро­чем, в большинстве случаев это отличие несущественно. График функции единичного скачка приведен на рис.7 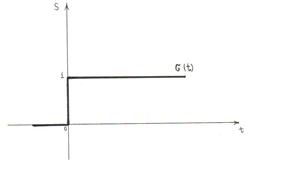Функцию единичного скачка удобно использовать при создании математических выражений для сигналов конечной длительности. Простейшим примером является формирование прямоугольного импульса с амплитудой А и длительностью Т: S(t)=A(σ(t)- σ(t-T))

Вообще, любую кусочно-заданную зависимость можно записать в виде единого математического выражения с помощью функции единичного скачка.

Основная литература: 2[18-24]; 6[43-47];

Контрольные вопросы:

1. Что понимают под детерминированным сигналом.

2. Разновидности математических представлений детерминированных сигналов.

3. Запишите условия ортонормированности и ортогональности системы функций.

4. Почему необходимо изучение моделей детерминированных сигналов..

5, Опишите временную форму представления сигналов.

Дата добавления: 2014-01-03; Просмотров: 1170; Нарушение авторских прав?; Мы поможем в написании вашей работы!