Уравнение модели

Фактор "бета" как измеритель недиверсифицируемого риска используется в модели оценки доходности активов (САРМ) для определения требуемой нормы доходности инвестиций в соответствии со следующим уравнением:

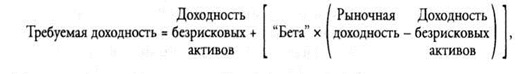
где требуемая доходность — это требуемая доходность инвестиций при данном уровне риска, измеренного с помощью фактора "бета";

доходность безрисковых активов — это доходность, которая может быть получена на свободные от риска инвестиции, обычно измеряемая как доходность векселей Казначейства США;

рыночная доходность — это средняя доходность всех ценных бумаг (обычно измеряется средней доходностью всех ценных бумаг, включаемых в составной фондовый индекс "Стэндард энд пур'з 500" или какой-либо другой всеобъемлющий фондовый индекс);

разность (рыночная доходность – доходность безрисковых активов) называют премией за риск.

Следует отметить, что требуемая доходность для данной ценной бумаги растет с увеличением ее фактора "бета" *.

Применение модели может быть проиллюстрировано следующим примером. Предположим, ценная бумага с фактором "бета" 1,25 рассматривается в тот момент, когда ставка безрисковых активов составляет 6%, а рыночная доходность — 10%. Подставляя эти данные в уравнение САРМ, получаем:

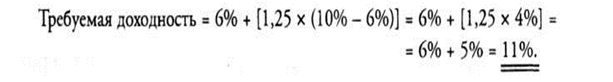
Таким образом, инвестору следовало бы ожидать доходности данных инвестиций в 11 % в качестве компенсации за риск, который приходится допускать при значении фактора "бета" 1,25. Если бы фактор "бета" был ниже, скажем равнялся 1, то требуемая доходность составила бы 10%

6% + [1,0×(10% - 6%)] = 10%,

а если бы фактор "бета" был выше, скажем, равнялся 1,5, то требуемая доходность составила бы 12%

6% + [1,5×(10% - 6%)] = 12%.

Понятно, что модель отражает прямые функциональные связи между риском и доходностью, поскольку, чем выше риск ("бета"), тем выше требуемая доходность.

Дата добавления: 2014-01-03