Статистический смысл второго начала термодинамики

Состояние термодинамической системы может быть задано значением ее параметров – температуры, давления, объёма, внутренней энергии и т.п., характеризующих систему как целое. Это макросостояние системы. Если состояние макроскопического тела задано столь подробно, что известны состояния всех образующих тело молекул, то такое состояние называется микросостоянием. Любое макросостояние может быть задано разными способами, каждому из которых соответствует некоторое микросостояние. Число различных микросостояний, соответствующих данному макросостоянию, называется термодинамической вероятностью или статистическим весом макросостояния. Таким образом, термодинамическая вероятность – это число способов, которыми может быть осуществлено данное макросостояние.

Некоторое представление о статистическом весе можно получить, рассмотрев способы, которыми молекулы могут быть распределены между двумя половинками сосуда с газом. Возьмем случай, когда в сосуде, разделенном на две одинаковые половины А и В (рис.5.10), находится число молекул N= 4. Перенумеруем их: 1,2,3.4. Каждая молекула с равной вероятностью может находиться как в половине А, так и в половине В. Значит, вероятность того, что любая молекула окажется в половине А, равна 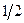. Пребывание в половине А одной молекулы и одновременно другой – события статистически независимые. Поэтому вероятность одновременного пребывания в половине А двух молекул равна произведению вероятностей, т.е.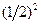, трех молекул - 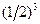, четырех - .

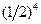Подобные рассуждения приводят к выводу, что вероятность любого размещения четырех молекул равна 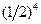. Каждое размещение - это некоторое микросостояние системы, и вероятность Р каждого из них одинакова и равна .

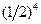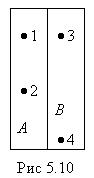
Например, макросостояние, соответствующее трем молекулам слева и одной справа (рис.5.10) может быть осуществлено одним из следующих микросостояний:

слева справа

№ 1,2,3 № 4

№ 2,3,4 № 1

№ 1,3,4 № 2

№ 1,2,4 № 3,

то есть четырьмя способами. Статистический вес этого макросостояния равен 4. Все 4 микросостояния равновероятны. Вероятность каждого микросостояния .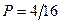

Макросостояние, у которого в обеих половинах сосуда находится одинаковое число молекул (по две), реализуется с помощью шести микросостояний, т.е. статистический вес (а также вероятность) такого макросостояния состояния максимальна.

Пусть первоначально все четыре молекулы находились в половине сосуда А. С течением времени некоторые из молекул, двигаясь беспорядочно, окажутся в половине В. Это будет означать, что газ расширился. В дальнейшем макросостояние системы будет меняться случайным образом, но чаще будет осуществляться то из них, вероятность которого больше, т.е. состояние с максимальным статистическим весом 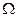.Может произойти так, что случайно все четыре молекулы снова окажутся в половине А сосуда (газ самопроизвольно сжался), т.е. процесс расширения оказывается обратимым.

Вследствие статистической независимости поведения молекул идеального газа вероятность любого макросостояния равна произведению вероятностей пребывания молекулы в любой половине сосуда. Для N частиц это произведение 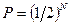, и полное число микросостояний системы равно 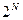. С ростом N вероятность самопроизвольного сжатия газа в одной половине резко уменьшается. Вместе с тем статистический вес (и вероятность) макросостояния, при котором молекулы распределяются равномерно по обеим половинам сосуда, стремительно растет с ростом N.

Таким образом, предоставленная самой себе макросистема стремится переходить от менее вероятных состояний к более вероятным. В этом суть необратимости. В принципе обратимый процесс возможен, но его вероятность ничтожно мала.

Рассмотрим макросостояние, при котором в одной половине сосуда находится п молекул, а в другой N-n. Число микросостояний (способов), которыми может быть реализовано такое макросостояние числу перестановок N молекул, т.е. N!. Однако перестановки, при которых изменяется только порядок размещения в первой половине (п!) не приводит к новому микросостоянию. Каждому из возможных распределений отдельных молекул во второй половине сосуда соответствует п! различных размещений молекул в первой половине. Поэтому, разделив полное число перестановок N! на п!, мы исключим перестановки, которые различаются лишь способом размещения молекул в первой половине сосуда. Разделив затем это выражение на (N-n)!, мы исключим перестановки во второй половине сосуда. В результате число распределений молекул по обеим половинам сосуда, отличающихся лишь номерами молекул в обеих половинах, равно

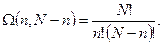
Это число микросостояний, соответствующих макросостоянию (n, N - n), т.е. статистический вес данного макросостояния. При наиболее вероятном распределении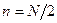

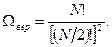
Соответствующая вероятность .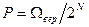

Если макросистема находится в неравновесном состоянии, то она самопроизвольно будет переходить в состояние с большей вероятностью – равновесное.Вместе с тем, согласно второму началу термодинамики все самопризвольные процессы сопровождаются возрастанием энтропии. Поэтому между энтропией и вероятностью в каждом состоянии должна быть связь. Для нахождения этой связи рассмотрим необратимый процесс расширения идеального газа в пустоту. Первоначально газ находится в объеме 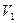теплоизолированного сосуда объемом 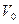(рис.5.11). От остальной части сосуда он отделен перегородкой. Перегородку

практически мгновенно перемещают из положения 1 в положение 2, газ расширяется в пустоту до объема 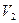и приходит в равновесное состояние. При этом работу газ не совершает, А =0, переданное газу тепло равно нулю, 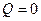, и по первому началу термодинамики приращение внутренней энергии равно нулю, 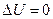, т.е. температура начального и конечного состояний одинакова.

Так как энтропия – функция состояния, ее приращение в этом процессе вычислим по обратимому процессу, например, по изотермическому, теплота 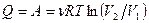, поэтому изменение энтропии

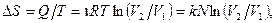
где 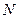- число молекул в газе.

В рассмотренном процессе распределение по скоростям в начальном и конечном состояниях одинаково (так как температура не изменилась). Пространственное же распределение молекул стало более “свободным”, значит, более вероятным. Действительно, вероятность нахождения одной молекулы газа в объеме 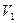равна 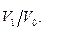Вероятность всех N молекул собраться в объеме 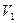равна 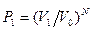. В объеме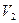 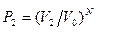. Отношение этих вероятностей 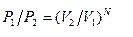, тогда приращение энтропии

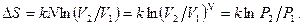
Вероятность макросистемы пропорциональна статистическому весу, 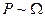, тогда

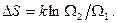
и энтропия

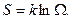
Это формула Больцмана, связывающая энтропию (чисто физическую величину) со статистическим весом.

Рассмотрим макросистему, состоящую из двух невзаимодействующих подсистем, одна из которых находится в состоянии 1 с энтропией 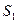и статистическим весом 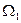, а другая – в состоянии 2 с энтропией 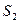и статистическим весом 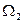. Число способов (микросостояний), реализующих рассматриваемое макросостояние, равно 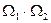. Тогда

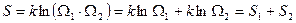
- энтропия системы равна сумме энтропий ее частей, т.е. энтропия _ величина аддитивная.

Принцип возрастания энтропии со статистической точки зрения привел Больцмана к фундаментальному выводу:

Все замкнутые макросистемы стремятся переходить от состояний менее вероятных к более вероятным.

При этом сама энтропия 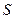характеризует степень беспорядка в макросистеме: состояниям с большим беспорядком отвечает большая вероятность (статистический вес), чем у более упорядоченного состояния.

Чем выше степень беспорядка в координатах и скоростях частиц, тем больше вероятность Ω того, что система будет находится в состоянии беспорядка. Система находится в состоянии с большей вероятностью чаще, чем в состоянии с меньшей вероятностью. Система, первоначально находившаяся в состоянии с малой вероятностью, будет стремиться к состоянию, в котором вероятность больше. С ростом термодинамической вероятности растёт энтропия S, поэтому изменение энтропии должно быть положительным dS >0. Энтропия изолированной системы при протекании необратимого процесса возрастает, т.е. изолированная система переходит из менее вероятных состояний в более вероятные, поэтому величина S растёт. Энтропия системы, находящейся в равновесном состоянии, максимальна.

Учитывая сказанное, можно придти к уточнённой формулировке закона возрастания энтропии:

При всех происходящих в замкнутой системе тепловых процессах энтропия системы возрастает, максимально возможное значение энтропии замкнутой системы достигается в тепловом равновесии.

Обратно можно сказать, что всякий процесс, при котором энтропия замкнутой системы тел возрастает, является необратимым. Чем больше возрастание энтропии, тем больше степень необратимости. Идеальному случаю полностью обратимого процесса соответствует случай, когда энтропия замкнутой системы оставалась бы постоянной.

Энтропия является количественной мерой степени молекулярного беспорядка в системе, т.е. степенью неопределённости системы. Если число способов мало, состояние называется упорядоченным или неслучайным. Сообщение системе тепла приводит к усилению теплового движения молекул, т.е. к увеличению степени беспорядка в системе, чем выше Т (а значит, и внутренняя энергия), тем относительно меньшей оказывается доля беспорядка, обусловленного сообщением тепла 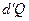. Если тепло 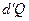сообщается системе в ходе необратимого процесса, энтропия возрастает как вследствие сообщения тепла, так и вследствие необратимости процесса, поэтому для необратимого процесса 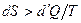, для обратимого 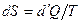. Объединяя оба выражения, получаем 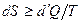- это основное термодинамическое неравенство. Оно объединяет запись закона сохранения энергии и закона возрастания энтропии и представляет собой объединённую запись первого и второго начал термодинамики.

В замкнутой системе энтропия отдельного тела может уменьшаться, это не противоречит второму началу термодинамики, т.к. оно применимо лишь к замкнутым системам. При совместном рассмотрении всех частей системы полное изменение энтропии либо равно нулю, либо положительно. Деятельность человека на земле приводит к локальному уменьшению энтропии. Холодильники и тепловые насосы способны перекачивать тепло от холодного тела к горячему. Жизнь как биологическое явление характеризуется процессами, уменьшающими локальную энтропию. Всюду, где наблюдается локальное возрастание упорядоченности, противостоящее беспорядку, происходит локальное убывание энтропии. Однако полная система, включающая в себя первоисточник – Солнце, характеризуется возрастанием суммарной энтропии.

Второе начало термодинамики является фундаментальным (основным) законом физики. Однако все фундаментальные законы (закон сохранения импульса, энергии и т.п.) были симметричны относительно обращения времени (т.е. при обращении движения всех частиц справедливы те же уравнения и законы). Второе же начало термодинамики несимметрично относительно обращения времени. Действительно, рассмотрим систему, состоящую из двух сосудов равного объёма, первый сосуд заполнен газом, второй – пустой. Уберём перегородку, разделяющую сосуды. Газ заполнит оба сосуда равномерно. Сколько бы мы ни ждали, обратного процесса не произойдёт. Теперь предположим, что после заполнения газом обоих сосудов время остановилось и пошло в обратном направлении. Такую картину можно получить, если процесс заснять на киноплёнку, а потом прокрутить задом наперёд. При этом сосуд 2 самопроизвольно пустеет и в нём возникает вакуум. Перед нами парадокс. Мы наблюдаем специфическую конфигурацию координат частиц и их скоростей в сосуде 2, которая вынуждала бы частицы двигаться и сталкиваться таким образом, чтобы все они в конечном счёте вылетали бы из сосуда 2, при этом ни один физический закон не нарушается. Парадокс устраняется тем, что кроме этой частной конфигурации частиц в сосуде 2 существует бесчисленное множество других конфигураций, при которых частицы распределены в обоих сосудах почти поровну. Поэтому на практике подобная начальная конфигурация, приводящая к вакууму в сосуде 2, хотя и допустима, но никогда не случается. Следовательно, процесс расширения газа в вакуум необратим несмотря на то, что в принципе такое «спонтанное» образование вакуума возможно.

Дата добавления: 2014-01-03