Некоторые законы распределения, используемые в метрологической практике

Распределение Стьюдента, (t-распределение) появляется в двух случаях: при оценке ряда наблюдений и интерпретации данных, приводимых в сертификатах о калибровке.

Если имеется серия из n независимых наблюдений 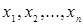случайной величины, подчиняющейся нормальному распределению с неизвестным математическим ожиданием 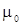и неизвестной дисперсией 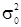, , 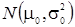и за выходную величину Х принимают оценку математического ожидания 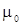, то, приписывая 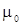и 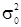совместное неинформативное априорное распределение и используя теорему Байеса, можно получить безусловно одномерное распределение для Х, которым в данном случае будет масштабированное смещенное t -распределение 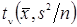с с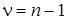тепенями свободы, где

,

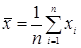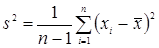
представляют собой выборочное среднее и выборочную дисперсию соответственно.

Плотность распределения вероятностей для Х имеет вид:

,

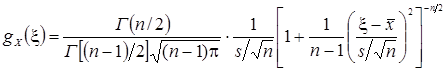где 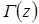– гамма-функция: .

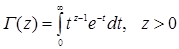Математическое ожидание и дисперсия Х имеют вид:

, ,

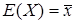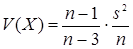где Е (Х) определено только для 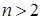, а V (X) – только для 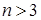. Таким образом, наилучшая оценка Х и соответствующая ей стандартная неопределенность имеют вид:

, .

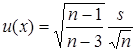Для формирования выборки значений случайной величины, подчиняющейся распределению 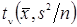, выбирают значения t случайной величины, подчиняющейся центральному t -распределению с 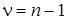степенями свободы и формируют:

.

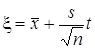Если вместо оценки стандартного отклонения s, вычисленной по одной выборке наблюдений, используют объединенную оценку стандартного отклонения 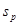с с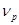тепенями свободы, полученную по Q сериям наблюдений:

, ,

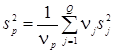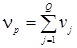то число степеней свободы 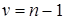для масштабированного смещенного t -распределения, приписанного Х, необходимо заменить числом степеней свободы 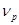для объединенной оценки стандартного отклонения 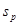. В результате плотность распределения вероятности:

,

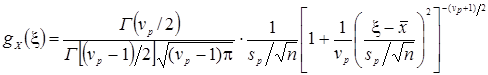а , .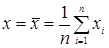

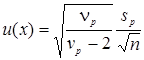Если источником информации о величине Х является сертификат о калибровке, в котором указаны наилучшая оценка х, расширенная неопределенность 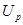, коэффициент охвата 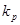и число эффективных степеней свободы 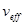, то величина Х может быть описана масштабированным смещенным t -распределением 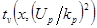с степенями свободы.

Если 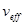бесконечно или неопределенно, то Х может быть приписано нормальное распределение .

Равномерное распределение (рис. 3.3). Если единственной доступной информацией о величине Х являются нижняя a и верхняя b (a < b) границы возможных значений этой величины, то случайную величину Х следует описывать равномерным распределением R (a, b) на интервале [ a, b ].

Плотность распределения вероятностей для Х имеет вид:

.

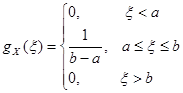Математическое ожидание и дисперсия Х имеют вид:

, .

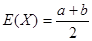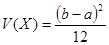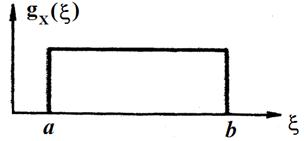
Рис 3.3. Равномерное распределение

Трапециевидное распределение (рис. 3.4 а). Если случайная величина Х является суммой двух независимых случайных величин Х ₁ и Х ₂, каждая из которых подчиняется равномерному распределению R (a_i, b_i) с нижней границей a_i и верхней границей b_i (i = 1,2), то Х подчиняется симметричному трапецеидальному распределению Trap (a, b, β) с нижней границей a, верхней границей b и параметров β, равным отношению длины верхнего основания трапеции к длине ее нижнего основания. Параметры трапецеидального распределения связаны с параметрами равномерного распределения соотношениями:

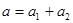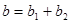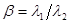, , , (3.7)

где 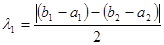, , 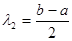. (3.8)

Плотность распределения вероятностей Х, полученная в результате свертки двух распределений имеет вид:

где .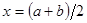

Математическое ожидание и дисперсия имеют вид:

, .

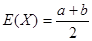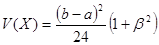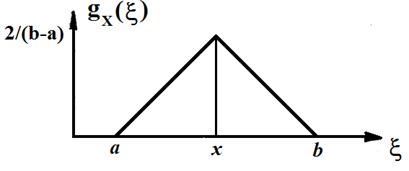
Треугольное распределение (закон Симпсона). Это распределение (рис. 3.4 б) является частным случаем трапецеидального, когда составляющие имеют одинаковые равномерные законы распределения и 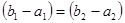, то из выражений (3.7) и (3.8) следует, что 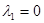и . Таким образом, трапецеидальное распределение Trap (a, b, 0) превращается в симметричное треугольное распределение Т (a, b) на интервале [ a, b ].

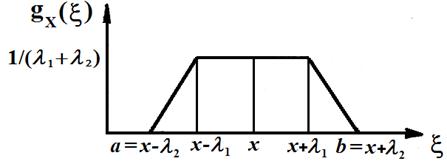
а

б

Рис. 3.4. Трапециевидное (а) и треугольное (б) распределения

Плотность распределения имеет вид:

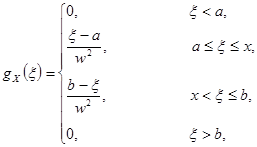
где 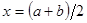и .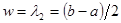

Математическое ожидание и дисперсия имеют вид:

, .

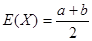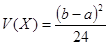Классификация средств измерений

Средство измерений (СИ) – техническое устройство, предназначенное для измерений.

Средства измерений используются для определения величин, единицы которых допущены в установленном порядке к применению в Российской Федерации и должны соответствовать условиям эксплуатации и установленным требованиям. Решения об отнесении технического устройства к средствам измерений и об установлении интервалов между поверками принимает Росстандарт России.

К средствам измерения относятся:

1) меры - средства измерения, предназначенные для воспроизведения и/или хранения физической величины одного или нескольких заданных размеров, значения которых выражены в установленных единицах и известны с необходимой точностью. Иногда к ним относят стандартные образцы и стандартные вещества;

2) измерительные преобразователи – технические средства с нормированными метрологическими характеристиками, служащие для преобразования измеряемой величины в другую величину или измерительный сигнал, удобный для обработки, хранения, дальнейших преобразований, индикации или передачи.

3) первичный измерительный преобразователь - измерительный преобразователь, на который непосредственно воздействует измеряемая физическая величина, т.е. первый преобразователь в измерительной цепи измерительного прибора (установки, системы).

Первичные измерительные преобразователи, размещаемые непосредственно на объекте исследования и в удалении от места обработки, отображения и регистрации измерительной информации, называют иногда датчиками;

промежуточный измерительный преобразователь - преобразователь, занимающий в измерительной цепи место после первичного;

Измерительные преобразователи в зависимости от вида входного и выходного сигналов относят к одной из следующих групп: а) аналоговые измерительные преобразователи, у которых на входе и на выходе аналоговые сигналы; б) аналого-цифровые измерительные преобразователи, имеющие на входе аналоговый сигнал, а на выходе кодированный сигнал; в) цифро-аналоговые измерительные преобразователи, у которых на входе кодированный сигнал, а на выходе аналоговый (квантованный) сигнал;

4) измерительные приборы - средства измерения, предназначенные для получения значений измеряемой физической величины в установленном диапазоне.

Измерительным прибором называют средство измерений, предназначенное для выработки сигнала измерительной информации в форме, доступной для непосредственного восприятия наблюдателем, например, в виде цифрового отсчета на отсчетном устройстве. Измерительный прибор, показания которого являются непрерывной функцией изменения измеряемой величины, называют аналоговым измерительным прибором. Например, электроизмерительный прибор с отсчетным устройством в виде стрелки и шкалы — аналоговый прибор.

Измерительный прибор, автоматически вырабатывающий дискретный (кодированный) сигнал измерительной информации и дающий показания в цифровой форме, называют цифровым измерительным прибором;

5) измерительные установки - совокупность функционально объединенных мер, измерительных приборов, измерительных преобразователей и других устройств, предназначенных для измерений одной или нескольких физических величин и расположенных в одном месте;

6) измерительные системы (ИС) - совокупность функционально объединенных мер, измерительных приборов, измерительных преобразователей, ЭВМ и других технических средств, размещенных в разных точках контролируемого объекта и т.п. с целью измерений одной или нескольких физических величин, свойственных этому объекту, и выработки измерительного сигнала в разных целях;

7) измерительно-вычислительные комплексы (ИВК) - функционально объединенная совокупность средств измерений, ЭВМ и вспомогательных устройств, предназначенных для выполнения в составе измерительной системы конкретной измерительной задачи;

8) измерительные принадлежности – вспомогательные средства, служащие для обеспечения нужных условий для выполнения измерений с необходимой точностью (источники питания, термостаты и т.д.).

По метрологическому назначению средства измерений делятся на:

1) рабочее средство измерений – средство измерений, предназначенное для измерений не связанных с передачей размера единицы другим средствам измерения (бывают лабораторные, производственные и полевые);

2) эталон единицы величины – средство измерений, предназначенное для воспроизведения и хранения единицы величины (или кратных либо дольных значений единицы величины) с целью передачи ее размера другим средствам измерений данной величины;

3) первичный эталон – эталон, обеспечивающий воспроизведение единицы с наивысшей в стране точностью;

4) исходный эталон – эталон, обладающий наивысшими метрологическими свойствами (в данной лаборатории, организации, на предприятии), от которого передают размер единицы подчиненным эталонам и имеющимся средствам измерения;

5) государственный первичный эталон – первичный эталон, признанный решением уполномоченного на то государственного органа в качестве исходного на территории Российской Федерации.

Рабочие эталоны 1-го, 2-го, 3-го и 4-го разряда предназначены для передачи единицы величины рабочим СИ.

Государственные эталоны единиц величин используются в качестве исходных для воспроизведения и хранения единиц величин с целью передачи их размеров всем средствам измерений данных величин на территории Российской Федерации.

Государственные эталоны единиц величин являются исключительной федеральной собственностью, подлежат утверждению Росстандартом России и находятся в его ведении (ст. 7 Закон РФ «Об обеспечении единства измерений »).

Дата добавления: 2014-01-03