И передает пару чисел (r, е) абоненту В

Шаг 2. В, получив (r,е), вычисляет

m'= е r^p-1-c_Bmod р. (3.4)

Схема обмена ключами по алгоритму Эль-Гамаля представлена на рисунке 3.

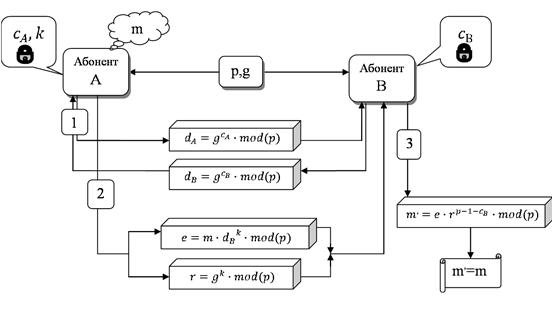
Рисунок 3 - схема обмена ключами в системе Эль-Гамаля

Ясно, что по аналогичной схеме могут передавать сообщения все абоненты в сети. Заметим, что любой абонент, знающий открытый ключ абонента В, может посылать ему сообщения, зашифрованные с помощью открытого ключа d_B. Но только абонент В, и никто другой, может расшифровать эти сообщения, используя известный только ему секретный ключ с_В. Отметим также, что объем шифра в два раза превышает объем сообщения, но требуется только одна передача данных (при условии, что таблица с открытыми ключами заранее известна всем абонентам).

Контрольные вопросы

1. Дайте краткую характеристику системы шифрования по алгоритму Эль-Гамаля.

2. Сколько секретных ключей генерируется для пересылки, например, трех сообщений между абонентами А и В?

3. Какими основными преимуществами обладает эта система перед другими?

Архивация файлов

При эксплуатации персональных компьютеров по самым различным причинам возможны порча или потеря информации на магнитных дисках. Это может произойти из-за физической порчи магнитного диска, неправильной корректировки или случайного уничтожения файлов, разрушения информации компьютерным вирусом и т.д. Для того чтобы уменьшить потери в таких ситуациях, следует иметь архивные копии используемых файлов и систематически обновлять копии изменяемых файлов. Для хранения архивов данных можно использовать внешние запоминающие устройства большой емкости, которые дают возможность легко скопировать жесткий диск

BBBBBLLLLLAAAAA
05 B 06 L12 A вместо 15 повторяется 9 байт

Эти последовательности можно интерпретировать следующим образом: с первой позиции 5 раз повторяется знак В, с шестой позиции 5 раз повторяется знак L и с позиции 11 повторяется 5 раз знак А. Согласитесь, очень простая демонстрация алгоритма архивации.Очевидно, что для хранения файла в его последней форме требуется лишь 9 байт - меньше на 6 байт.Описанный метод является простым и очень эффективным способом сжатия файлов. Однако он не обеспечивает большой экономии объема, если обрабатываемый текст содержит небольшое количество последовательностей повторяющихся символов.

Список литературы

1.Романец Ю. В. Защита информации в компьютерных системах и сетях. /Под ред. В.Ф. Шаньгина. – М: Радио и связь 1999

2.Петраков А.В. Основы практической защиты информации. 2-е издание Учебн. Пособие. – М: Радио и связь 200

3. Рябко Б. Я., Фионов А.Н. Криптографические методы защиты информации. –М: Горячая линия- Телеком, 2005.

Дата добавления: 2014-01-03