Флуктуации термодинамических величин

Рассмотрим флуктуации, которые происходят в квазизамкнутой макроскопической системе А, погруженный в термостат В с температурой 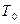(Т=< 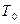>). Будем считать, что флуктуация происходит только в системе А, при этом термостат участвует в квазистатическом процессе. Состояние системы определяется параметром Х, который в состоянии равновесия равен нулю, а в конечном флуктуационном состоянии Х ¹0. Пусть изменение Х происходит достаточно медленно, поэтому равновесие в системе А при флуктуации не нарушается. При изменении параметра Х изменяются так же значения термодинамических величин, которые могут быть определены из первого и второго начал термодинамики.

Процесс перехода макроскопической системы из начального состояния в конечное (флуктуацию) можно рассматривать как действие некоторого воображаемого источника работы. Работу этого источника при изменении Х от 0 до Х обозначим D А(Х). Полное изменение энтропии замкнутой системы, состоящей из термодинамической системы А и термостата В, равно:D S=DS_A + DS_{B ,} D S_A - изменение энтропии системы А, D S_B - изменение энтропии термостата В.

Для определения изменения энтропии D S_A системы А, в которой возможна флуктуация параметра Х, обозначим работу внешнего источника D А, тогда изменение энтропии системы согласно основному термодинамическому неравенству будет равно

.

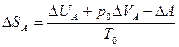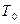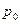Здесь и - равновесные значения температуры и давления системы А, 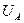- внутренняя энергия, 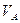объем системы А, 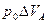- работа, совершаемая системой (или над системой).

Аналогично, изменение энтропии термостата равно: .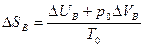

Система А и термостат В образуют замкнутую систему, поэтому выполняются законы сохранения объема (при постоянном давлении, p=const) 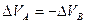и энергии 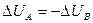. Тогда полное изменение энтропии .

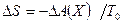Подставив это выражение в функцию распределения величины Х, имеем:

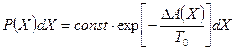
- мерой вероятности малых флуктуаций в макроскопической системе А является работа, которую надо над ней совершить для изменения параметра х от нуля до некоторого значения. Величина работы D А количественно определяет меру флуктуации.

Определим величину этой работы. Ввиду малости флуктуации переход системы из начального в конечное состояние будем считать равновесным, тогда

D A =D U _A - 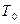D S _A + p _OD V _A.

Рассмотрим изотермический процесс, 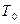= const. В этом случае

D A =D(U_A - 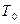S)+ p_O D V _A,

величина U_A - 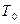S_A=F_A - свободная энергия (или термодинамический потенциал Гельмгольца) макроскопической системы А, тогда d(U - TS)=dF= -pdV, или 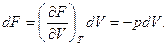Отсюда

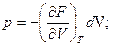(5.1)

но D A =D F+p_O D V, следовательно,

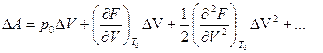(5.2)

(D F разложили в ряд). Подставляя (6.1) в (6.2) имеем:

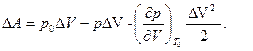(5.3)

Флуктуация рассматривается как равновесный процесс, поэтому 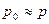, и

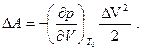(5.4)

Тогда вероятность того, что обьем системы находится между V и V+dV равна:

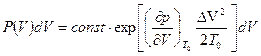. (5.5)

Из (6.5) следует, что производная 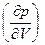должна быть отрицательной. Если бы это условие не выполнялось, вероятность флуктуации не убывала бы с ростом ее масштаба и система находилась бы в неустойчивом состоянии.

Таким образом, первое условие устойчивости состояний имеет вид

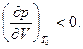(5.6)

Если это условие выполняется, то постоянная, входящая в (5.5) равна:

.

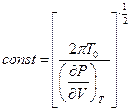Найдем теперь распределение вероятности, определяющее флуктуацию температуры при постоянном объеме. Для этого определим работу, которую нужно совершить над системой А для того, чтобы перевести ее из начального состояния с постоянной температурой 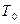в конечное с температурой 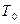+ dT. Для изменения энтропии имеем:

,

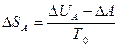т.к. 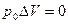, тогда .

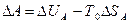Разложим изменение внутренней энергии D U в ряд по малым степеням DS, учитывая, что 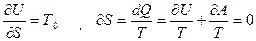, получаем

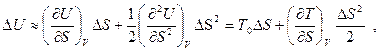но 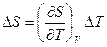, тогда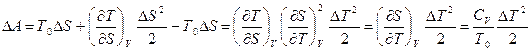

(здесь учли определение теплоемкости C_V=DQ_V/DT и D Q_V=TDS).

Вероятность того, что температура макроскопической системы А испытывает флуктуацию и меняется в интервале T, T+dT равна

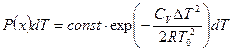. (5.7)

Из выражения (6.7) следует второе условие устойчивости состояний:

C_V> 0 - теплоемкость однородного вещества при постоянном объеме должна быть существенно положительной величиной.

Дата добавления: 2014-01-03