Примеры самоорганизации в неживой природе

Самоорганизация в химических системах связана с поступлением извне новых веществ, которые обеспечивают продолжение реакции, и выведением в окружающую среду отработанных. Например, окисление органической (малоновой) кислоты бромидом калия. При добавлении индикатора окислительно-восстановительных реакций (ферроина) можно наблюдать за ходом реакции по периодическому изменению цвета раствора. Внешне самоорганизация проявляется появлением в жидкой среде концентрических волн или в периодическом изменении цвета раствора с синего на красный и наоборот. Этот колебательный процесс идет без всякого вмешательства извне в течение нескольких десятков минут и получил название «химических часов».

Колебания происходят около неустойчивого стационарного состояния вдали от состояний равновесия. (Около устойчивых стационарных состояний такие периодические колебания невозможны).

Самоорганизация в социальных системах. Основоположник классической политической экономии А. Смит (1723-1790) в своем главном труде «Исследование о природе и причинах богатства народов» показал, что спонтанный порядок на рынке является результатом взаимодействия различных, часто противоположных стремлений, целей и интересов его участников. Такое взаимодействие приводит к установлению никем не запланированного порядка, который выражается в равновесии спроса и предложения. А. Смит использовал метафору «невидимой руки», которая регулирует цены на рынке.

Подобные же идеи высказывались в то время и относительно самоорганизации норм нравственности в обществе. При этом идеи самоорганизации, самосовершенствования деятельности социальных систем связывались с эволюционными процессами.

Итак, следует выделить основные условия и положения самоорганизации систем:

- Система должна быть открытой, диссипативной и находиться вдали от термодинамического равновесия;

- если в случае закрытых систем самоорганизация (эволюция) ведет к росту энтропии и беспорядка, то в случае открытых систем происходит возникновение и усиление порядка через флуктуации. Именно флуктуации приводят в этом случае к «расшатыванию» старого порядка и возникновению нового. Энтропия падает, количество информации (негэнтропия растет).

- Самоорганизация открытых систем опирается на принцип положительной обратной связи, согласно которому изменения, появляющиеся в системе, не устраняются, а наоборот, накапливаются и усиливаются, что приводит к возникновению нового порядка и структуры.

- Система должна обладать достаточным количеством взаимодействующих между собой элементов и, следовательно, иметь некоторые критические размеры. В противном случае коллективное поведение элементов системы может не проявиться (самоорганизация не наступает).

- Чем выше в своем эволюционном развитии находится система, тем более сложными и многочисленными будут факторы, которые влияют на ее самоорганизацию. Представляется вероятным, что именно нелинейные открытые диссипативные системы лежат в основе большинства физических, биологических, социальных явлений. Научная картина мира включает в себя принцип единства, проявляющийся в существовании законов, справедливых для самых разнообразных уровней существования, от микромира до Метагалактики, от неживой природы до человека и общества. В классической науке такими законами были, например, закон сохранения энергии, второе начало термодинамики... В современной постклассической науке ими могут стать законы коэволюции нелинейных открытых диссипативных систем.

6. Флуктуации. Общие сведения о флуктуациях

Согласно второму началу термодинамики, самопроизвольные процессы ведут систему к наиболее вероятному состоянию - к возрастанию энтропии. После того, как энтропия системы стала максимальной, дальнейшие изменения в системе прекращаются - достигнуто равновесие.

Однако состояние равновесия совсем не означает внутреннего покоя; внутри системы проходят непрерывные тепловые движения. Таким образом, любое физическое тело в каждое мгновение перестает быть самим собой, взаимное расположение молекул в каждое мгновение не такое, как в предыдущее, и значения всех физических величин сохраняются лишь в среднем, они не строго равны своим вероятным значениям, а колеблются около эти значений.

ФЛУКТУАЦИИ (от лат. fluctuatio — колебание)- это случайные отклонения физических величин от их средних значений. Они происходят у любых величин, зависящих от случайных факторов. В статистической физике флуктуации вызываются тепловым движением частиц системы. Флуктуации определяют теоретически возможный предел чувствительности приборов. Флуктуации давления проявляются, например, в броуновском движении малых частиц под влиянием точно не скомпенсированных ударов молекул окружающей среды. Флуктуации характерны для любых случайных процессов.

Рассмотрим физическую величину, истинное значение которой равно Х, ее среднее значение < X >, тогда отклонение D Х=Х - <X> не может быть мерой флуктуации, оно меняется во времени, величина же < X >=0, т.к. имеют место равновероятные отклонения в обе стороны.

Мерой флуктуации физической величины Х является средняя величина квадрата разности D Х

<(D X)²>=<(X - < X >)²>=< X ²> - (< X >)^2,

которая называется квадратичной флуктуацией, <(D X)²> ³0.

Абсолютной флуктуацией называется величина .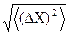

Относительная флуктуация - это отношение абсолютной флуктуации к среднему значению .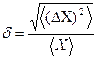

Флуктуации заметны для систем с небольшим числом частиц и совсем незаметны для больших тел с огромным числом молекул.

Исследования показали, что изменение плотности, давления и температуры газа, находящегося в 1 см³, составляет 10^-8 %. Такие флуктуации слишком малы, чтобы их можно было обнаружить опытом.

Иначе обстоит дело в объеме кубического микрона. Здесь число частиц N =, и флуктуации достигают измеримых величин (сотые доли %).

Флуктуация представляет собой “ненормальное” явление в том смысле, что она приводит к переходу от более вероятного состояния к менее вероятному. Во время флуктуации тепло переходит от холодного тела к горячему, нарушается равномерное распределение молекул, возникает упорядоченное движение.

Хотя флуктуации возникают непрерывно, они не оказывают влияния на общий ход физических процессов, энтропия процессов возрастает.

Пусть Х - некоторая физическая величина, характеризующая замкнутую макросистему в целом (например, объем, температура). Будем считать, что из Х уже вычли среднее значение этой величины (например, Х=Т - <T>), поэтому < X >=0. Распределение вероятностей для энергии замкнутой системы дает формула Больцмана.

Вероятность того, что величина принимает значения в интервале X; X+dX, равна

Р(Х)dХ=const exp (S(Х)),

где S - энтропия системы в состоянии Х.

В состоянии 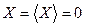энтропия системы S максимальна, поэтому

.

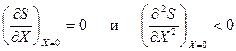Величина Х при флуктуации мала и функцию S(Х) можно разложить в ряд:

,

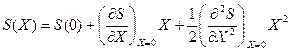или 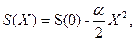где a = const >0, тогда

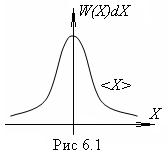
Р(Х)dХ=Aexp(- aХ²/2)dХ – это распределение Гаусса (рис.6.1).

Дата добавления: 2014-01-03