Способы нахождения мгновенного центра скоростей

В некоторых случаях из условия движения удаётся сразу указать точку плоской фигуры, скорость которой в рассматриваемый момент времени равна нулю. Эти точки и являются мгновенными центрами скоростей. В других наиболее общих случаях положения МЦС определяют, рассматривая параметры движения тела и ск о рости двух точек тела.

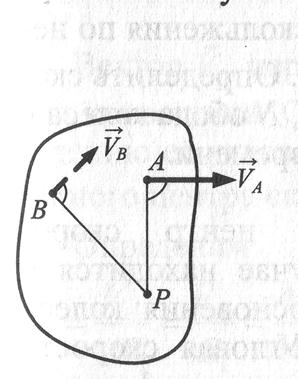
Вариант 1. Известна скорость точки А и направление скорости точки В. МЦС находится на пересечении перпендикуляров к скоростям, проведённых в точках А и В.

В этом случае

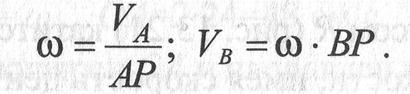
Вариант 2. Известна скорость точки А тела и угловая скорость 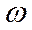. МЦС находится на перпендикуляре к вектору 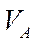в точке А на расстоянии АР АР=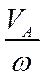

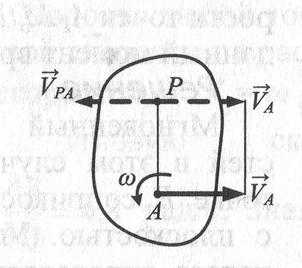
Вариант 3. Известны длина отрезка АВ, скорост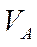и и 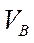двух точек тела, которые перпендикулярны к отрезку АВ и направлены в одну сторону

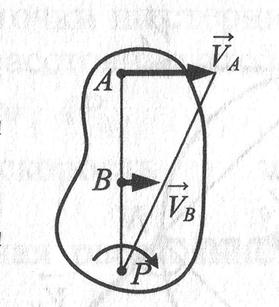
МЦС находится на продолжении отрезка АВ в точке пересечения с прямой, проведенной через концы векторов 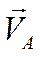и 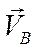. Для определения 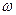составляем выражение

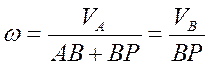, откуда .

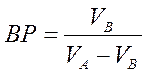Вариант 4. Известны длина отрезка АВ, скорост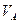ии 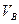двух точек тела, которые перпендикулярны отрезку АВ и направлены в разные стороны

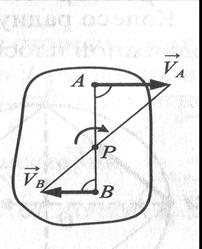
МЦС находится внутри отрезка АВ. Для определения 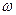составляем выражение

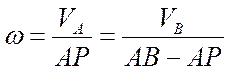, откуда.

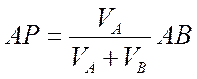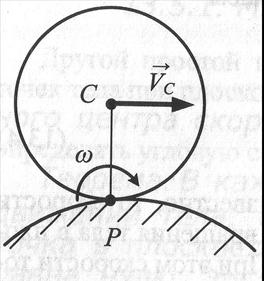
Вариант 5. На рис. тело перекатывается без проскальзывания по поверхности неподвижного тела. МЦС находится в точке соприкосновения тел в точке Р.

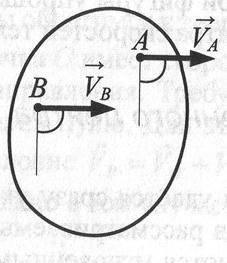
Вариант 6. На рис. скорости двух точек тела параллельны. В этом случае МЦС находится в бесконечности, т.е. отсутствует. Тело совершает мгновенное поступательное движение, тогда скорости двух точек и всех других точек тела одинаковы, а их ускорения в общем случае могут быть разными.

Задача 3. Колесо радиусом R катится без скольжения по неподвижной плоскости, имея скорость центра 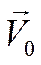. Определить скорости точек А, M, N обода колеса в данный момент времени.

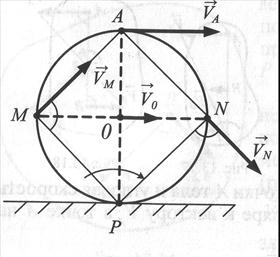
Решение.

Мгновенный центр скоростей в этом случае находится в точке Р соприкосновения колеса с плоскостью. Угловая скорость колеса определяется по формуле 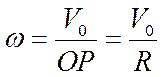. Скорости указанных точек определим с помощью МЦС: 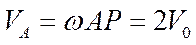; 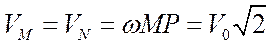, т.к. MP=NP=R.

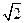Скорости точек колеса направлены по перпендикулярам к отрезкам прямых, соединяющих мгновенный центр скоростей с рассматриваемыми точками в направлении вращения.

Задача 4. Для механизма, изображенного на рис., найти скорости точек А, В, С, угловые скорости шатуна ВС и колеса 1 в момент времени, когда кривошип ОА находится в горизонтальном положении, а шатун ВС вертикален, если угловая скорость кривошипа 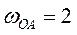рад/c; ОА=24 см; ВС=30 см; 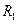=10 см.

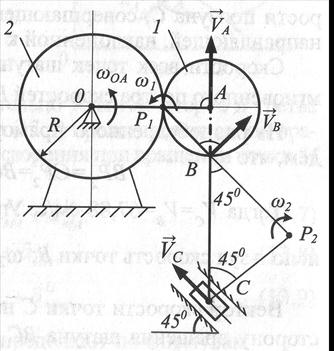
Для механизма, изображенного на рис., найти скорости точек А, В, С, угловые скорости шатуна ВС и колеса 1 в момент времени, когда кривошип ОА находится в горизонтальном положении, а шатун ВС вертикален, если угловая скорость кривошипа 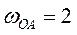рад/c; ОА=24 см; ВС=30 см; 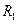=10 см.

Решение.

Заданный плоский механизм включает следующие звенья: кривошип ОА, подвижную шестерню 1, шатун ВС и ползун С. Шестерня 1 катится по поверхности неподвижной шестерни 2 без скольжения, совершая плоское движение, поэтому мгновенный центр скоростей 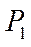шестерни 1 находится в точке их соприкосновения.

Используя угловую скорость кривошипа ОА, определим скорость точки А – конца кривошипа ОА и центра шестерни 1:

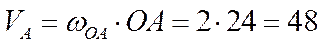см/c/

Вектор 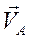перпендикулярен ОА и направлен в сторону вращения кривошипа. Скорость любой точки шестерни 1 равна произведению её угловой скорости на расстояние этой точки до мгновенного центра скоростей : =.

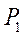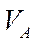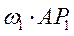Определим угловую скорость шестерни 1:

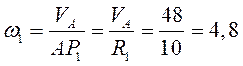рад/c. Зная расстояние от точки В до мгновенного центра скоростей (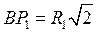), определим её скорость:

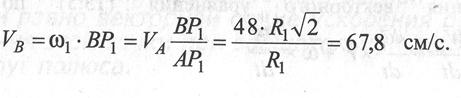
Скорость 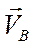направлена перпендикулярно отрезку 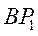в сторону вращения шестерни 1 вокруг мгновенного центра скоростей. Направление вращения шестерни 1 установим, исходя из направления скорости 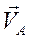, которая является вращательной скоростью относительно мгновенного центра скоростей 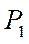. Шатун ВС совершает плоское движение. Мгновенный центр скоростей 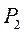шатуна находится в точке пересечения перпендикуляра к скорости точки В, являющегося продолжением отрезка 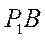, и перпендикуляра к скорости ползуна С, совершающего прямолинейное движение вдоль направляющей, наклоненной к горизонту под углом 45°.

Скорости всех точек шатуна являются вращательными вокруг мгновенного центра скоростей 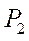, поэтому =; .

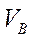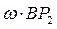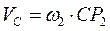Из равнобедренного прямоугольного треугольника 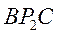найдём, что

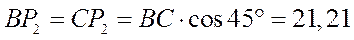см.

Тогда 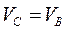=67,88 см/с. Угловую скорость шатуна ВС найдём используя скорость точки В: 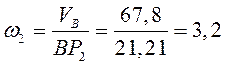рад/c.

Вектор скорости точки С направлен перпендикулярно к 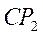в сторону вращения шатуна ВС вокруг мгновенного центра скоростей 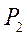. Направление вращения шатуна установим, исходя из направления скорости точки В, которая является вращательной скоростью относительно мгновенного центра скоростей .

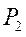Задача 5. В положении механизма, схема которого приведена на рис. 14, определить угловую скорость шатуна АВ и скорости точек В и С, если 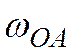= 2 рад/с, ОА = 0,2 м, АВ = 1,6 м, ВС = 0,8 м, h = 0,8 м.

Решение. Найдем скорость точки А:

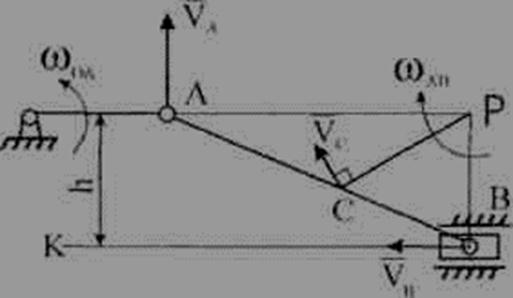
Рис. 14

Скорость ползуна В должна: быть направлена по прямой КВ. Мгновенный центр шатуна АВ находится в точке Р пересечения перпендикуляров. Восстановленных к направлениям векторов скоростей точек А и В.

Угловая скорость шатуна АВ равна

.

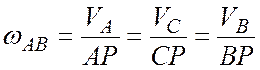Определим величины АР, ВР, СР:

,

.

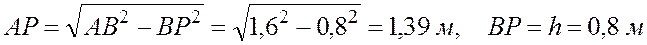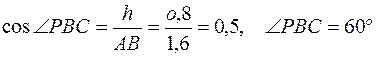Тогда 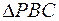равносторонний:

.

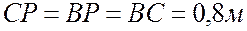Дата добавления: 2014-01-03