Эвристика выбора свойств на основе теории информации

Каждое свойство можно рассматривать с точки зрения его вклада в процесс классификации. Например, если необходимо определить виды животных, то одним из признаков классификации является откладывание яиц. Алгоритм при выборе корня текущего дерева оценивает удельный вес информации, добавляемой каждым свойством. Затем он выбирает свойство, имеющее наибольшую информативность. Теория информации обеспечивает математическую основу для измерения информативности сообщения. Каждое сообщение можно рассматривать как экземпляр в пространстве возможных сообщений. Передача сообщения соответствует выбору одного из возможных сообщений. С этой точки зрения целесообразно определить информативную емкость сообщения в зависимости от размера пространства и частоты использования каждого возможного сообщения.

Важную роль количества возможных сообщений можно оценить на примере азартных игр, сравнив ценность сообщения с правильным прогнозом результата вращения рулетки и подбрасывания монеты. Поскольку количество возможных состояний для рулетки значительно превышает количество результатов подбрасывания монеты, то правильный прогноз для игры в рулетку гораздо информативнее, тем более, что и ставки в этой игре значительно выше. Следовательно, такое сообщение несет больше информации. Роль вероятности передачи каждого сообщения видна из следующего примера.

Предположим, что существует монета, при подбрасывании которой в трех из четырех случаях выпадает решка. Если знать, что вероятность выпадения решки составляет 3/4, то в 3/4 случаев можно правильно угадать результат игры.

Шеннон формализовал эти наблюдения, определив количество информации в сообщении как функцию от вероятности р передачи каждого возможного сообщения, а именно- – log₂ p. Имея пространство сообщений М={m₁, m₂ …..m_n} и зная вероятности р(m_i) для каждого сообщения, информативность этих сообщений можно вычислить следующим образом:

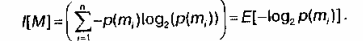
Количество информации в сообщении измеряется в битах. Например, информативность в сообщения в результате подбрасывания обычной монеты составляет

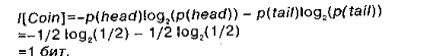
Если же монета такова, что вероятность выпадения решки составляет 75%, то информативность сообщения равна

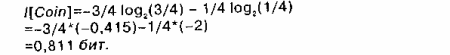
Это определение позволяет формализовать интуитивные рассуждения об информативности сообщений. Теория информации широко используется в компьютерных науках и телекоммуникациях, в том числе для определения информационной емкости телекоммуникационных каналов, при разработке алгоритмов сжатия данных и устойчивых к шуму коммуникационных стратегий. В алгоритме ID3 теория информации используется для выбора наиболее информативного свойства при классификации обучающим примером.

Дерево решений можно рассматривать с точки зрения информации о примерах. Информативность дерева вычисляется на основе вероятностей различных типов классификации. Например, если предположить, что все примеры в таблице 1 появляются с одинаковой вероятностью, то

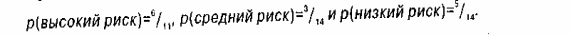
Следовательно, информативность распределения D₁ описанного в таблице 1, а значит и любого дерева, покрывающего эти примеры, составляет

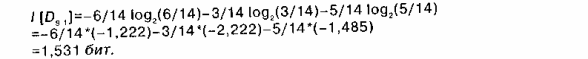
Количество информации, обеспечиваемое при выборе данного свойства в корне текущего дерева, равно разности общего количества информации в дереве и количества информации необходимого для завершения классификации. Количество информации необходимое для завершения дерева, определяется как взвешенное среднее ин­формации во всех его поддеревьях. Взвешенное среднее вычисляется как сумма произ­ведений информативности каждого поддерева и процентного соотношения примеров в этом поддереве.

Предположим, что существует набор обучающих примеров С. Если корнем текущего дерева является свойство Р, которое может принимать n значений, то множество С будет разделено на подмножества {С₁ С₂,.., С_n}. Информация, необходимая для завершения построения дерева при выборе свойства Р, составляет

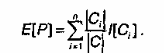
Выигрыш от использования свойства Р вычисляется как разность общей информатив­ности дерева и объема информации, необходимого для завершения построения дерева.

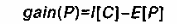
Возвращаясь к примеру из таблице 1, при выборе в качестве корня дерева свойства "доход" примеры будут разделены на три группы: С,={1,4,7, 11},С₂={2, 3, 12, 14} и С₃={5, 6, 8, 9, 10, 13}. Информация, необходимая для завершения построения де­рева, составляет

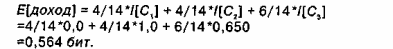
Информационный выигрыш от такого разбиения данных таблице1, составляет

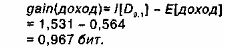
Аналогично можно показать, что

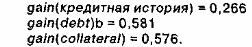
Поскольку доход обеспечивает наибольший информационный выигрыш, именно это свойство выбирается в качестве корня дерева решений алгоритма. Такой анализ ре­курсивно выполняется для каждого поддерева до полного построения всего дерева.

Дата добавления: 2014-01-03