
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Док-во (для «схемы случаев»)
|
|
|
|
Рассмотрим опыт, в котором могут произойти события А и В.
Обозначим: n – число возможных элементарных исходов для события А, m – для В; 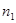 - число исходов, благоприятствующих А,
- число исходов, благоприятствующих А, 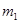 - благоприятствующих В.
- благоприятствующих В.
Очевидно, для события АВ число возможных элементарных исходов равно 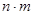 (т. к. любой исход для А может сочетаться с исходом для В)
(т. к. любой исход для А может сочетаться с исходом для В)
Число исходов, благоприятствующих АВ равно 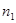
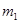
Р(АВ) = 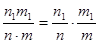 = Р(А) · Р(В).
= Р(А) · Р(В).
Теор. 4 Вероятность произведения конечного числа независимых событий равна произведению их вероятностей.
Доказывается методом математической индукции.
Следствие (другая формулировка)
Вероятность совместного появления нескольких независимых событий равна произведению их вероятностей.
Примеры 1) найти вероятность того, что при бросании двух монет 2 раза появиться герб(А)
Решение:
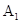 - появление «герба» при первом бросании,
- появление «герба» при первом бросании, 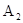 - при втором,
- при втором, 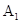 и
и 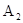 - независимы.
- независимы.
А = 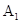 ·
·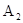 Р(А) = Р(
Р(А) = Р(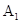 )Р(
)Р(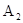 ) =
) = 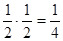 .
.
2) Две урны с шарами. В первой – 5 белых и 3 черных шара, во второй – один белый и 2 черных. Из каждой урны вытаскивают по шару. Найти вероятность того, что вытащат 2 былых шара.
Решение:
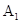 - вытащили белый шар из первой урны,
- вытащили белый шар из первой урны, 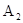 - из второй,
- из второй, 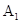 и
и 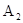 - независимы.
- независимы.
А = 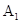 ·
·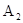 Р(А) = Р(
Р(А) = Р(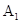 )Р(
)Р(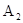 ) =
) = 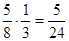
Теор. 5 (Умножения вероятностей зависимых событий)
Вероятность совместного появления двух зависимых событий равна произведению вероятности одного из них и условной вероятности второго, вычисленной в предположении, что первое уже произошло.
Р(АВ) = Р(А)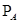 (В) = Р(В)
(В) = Р(В) 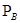 (А)
(А)
Доказательство (для «схемы случаев»)
Обозначим: n – число всевозможных элемент. исходов опыта, 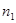 - число исходов, благоприятствующих А, m – благоприятствующих В при условии, что А наступило.
- число исходов, благоприятствующих А, m – благоприятствующих В при условии, что А наступило.
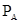 (В) =
(В) = 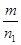 ; Р(АВ)=
; Р(АВ)= 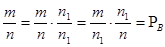 (А) · Р(А); Р(А) =
(А) · Р(А); Р(А) = 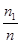
Пример В урне 3 черных и 2 белых шара, из нее 2 раза вытащим по шару. Найти вероятность того, что оба шара белые (А).
|
|
|
|
Дата добавления: 2014-01-03; Просмотров: 485; Нарушение авторских прав?; Мы поможем в написании вашей работы!