Комплексная форма ряда Фурье

Спектральное разложение периодического сигнала можно произвести используя комплексный ряд Фурье:

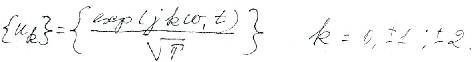
Функции этой системы периодичны с периодом T и ортонормированны на отрезке 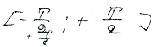т.к.

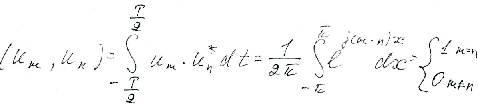
Ряд Фурье произвольно периодического сигнала принимает вид

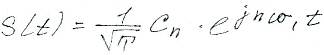
с коэффициентами

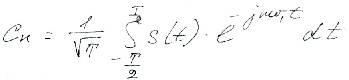
обычно используют следующую форму записи:

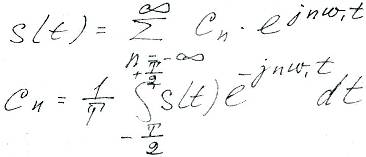
Спектр сигнала содержит компоненты отрицательной полуоси частот, причем С-n=C*n. В ряде слагаемых С (+) и (-) частотами объединяются в пары: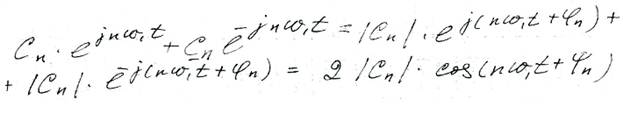

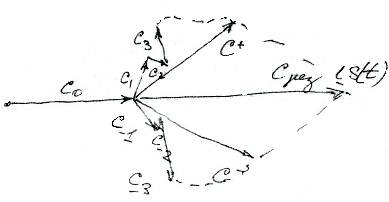
Структура ряда Фурье дает возможность изобразить периодический сигнал посредством бесконечной суммы вращающихся векторов на плоскости

2. Пусть S(t)- одиночный импульсный сигнал конечной длительности. Дополним его мысленно такими же сигналами периодически следующими через Т, получим изученную ранее периодическую последовательность Sпер(t), которая м.б. представлена в виде комплексного ряда Фурье:

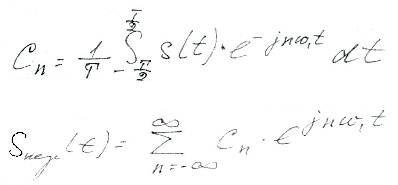
Для того чтобы вернутся к одиночному импульсу .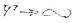

1. Частоты соседних гармоник nw1 и (n+1)w1 окажутся сколь угодно близкими так, что частоты nw1 можно заменить непрерывной w-текущей частотой. Воспользуемся тем, что коэффициенты ряда Фурье образуют комплексно-сопряженные пары:

Каждой паре соответствует гармоническое колебание

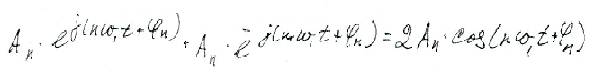
С комплексной амплитудой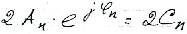

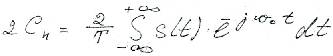
В результате находим комплексную амплитуду эквивалентного гармонического сигнала, отображающего вклад всех спектральных составляющих, содержащихся внутри интервала :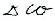

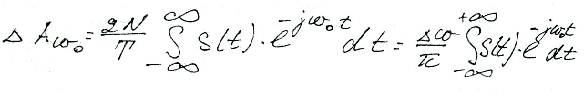
Функция

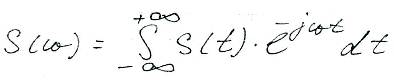
называется спектральной плотностью сигнала S(t)- это преобразование Фурье.

2. Физический смысл спектральной плотности.

Перейдем от w к f.

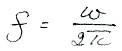
при этом

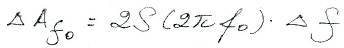
Спектральная плотность

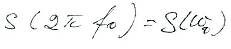
есть коэффициент пропорциональности между (длиной малого интервала частот) и отвечающей ей комплексной амплитуды 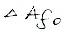гармонического сигнала, с частотой 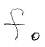.Коэффициент 2 означает, что вклад вносят и (+) и (-) частота 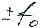. Спектральная плотность- комплексно

значная функция частоты, одновременно несущая информацию как об амплитуде, так и о фазе элементарных синусоид

Обратное преобразование Фурье:

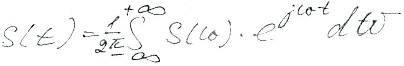
Метод спектральных разложений обогащает теорию сигналов. Например математическая модель представления функцией S(t) м.б. очень сложна и недостаточно наглядна. В то же время описание в частотной области посредством S(w) м.б. простым.

Дата добавления: 2014-01-03