
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Доказательство. Рассмотрим последовательность частичных сумм четного количества членов знакочередующегося ряда
|
|
|
|
Рассмотрим последовательность частичных сумм четного количества членов знакочередующегося ряда 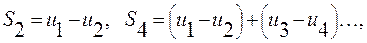
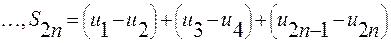
Каждая из разностей, стоящих в скобках, положительна по условию теоремы, значит, 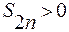 и последовательность
и последовательность 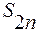 является возрастающей.
является возрастающей.
Если записать эту сумму в виде 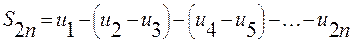 , то каждая из разностей в скобках положительна и
, то каждая из разностей в скобках положительна и 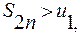 то есть последовательность
то есть последовательность 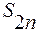 ограничена сверху.
ограничена сверху.
Итак, последовательность 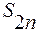 является возрастающей и ограничена сверху, следовательно, имеет предел
является возрастающей и ограничена сверху, следовательно, имеет предел 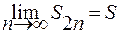 , причем
, причем 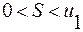 .
.
Аналогично можно показать сходимость последовательности частичных сумм нечетного количества членов знакочередующегося ряда, следовательно, ряд сходится.
Пример. Знакочередующийся ряд 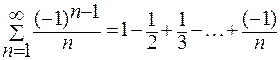 сходится условно по признаку Лейбница, так как
сходится условно по признаку Лейбница, так как 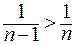 и
и 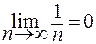 , но соответствующий ряд из абсолютных величин членов данного ряда является гармоническим
, но соответствующий ряд из абсолютных величин членов данного ряда является гармоническим 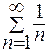 и расходится.
и расходится.
Ряд 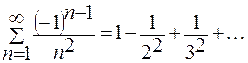 сходится абсолютно, так как этот знакочередующийся ряд сходится по признаку Лейбница, и ряд
сходится абсолютно, так как этот знакочередующийся ряд сходится по признаку Лейбница, и ряд 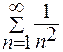 сходится тоже.
сходится тоже.
Замечание. Признак Лейбница используется для приближенного вычисления суммы знакочередующегося ряда с определенной точностью. Сумма отброшенных членов знакочередующегося ряда Лейбница не превосходит первого из них.
Пример. Сколько членов ряда нужно взять, чтобы сумму ряда 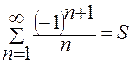 найти с точностью 0,001?
найти с точностью 0,001?
Представим сумму ряда в виде: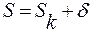 , где
, где 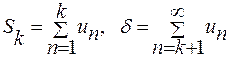 по признаку Лейбница.
по признаку Лейбница.
По условию задачи 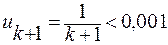 , откуда
, откуда 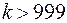 нужно взять
нужно взять 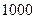 членов ряда.
членов ряда.
|
|
|
|
Дата добавления: 2014-01-03; Просмотров: 453; Нарушение авторских прав?; Мы поможем в написании вашей работы!