Расчетные данные

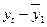
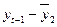
t	yt	yt-1		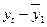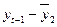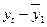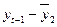	()()	()^2	()^2
		-	- -3,29 -3,29 -1,29 -0,29 0,71 2,71 4,71	- -3 -2 -2	- 9,87 6,58 2.58 0,71 5,42 18,84	- 10,8241 10,8241 1,6641 0,0841 0,5041 7,3441 22,1841	-
Итого						53,4287

Для данного примера средние значения составят:

=;

.

.

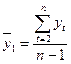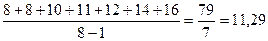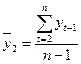
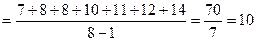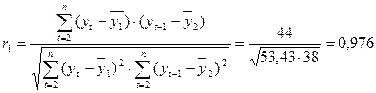Полученное значение свидетельствует об очень тесной зависимости между расходами на конечное потребление текущего и непосредственно предшествующих годов и, следовательно, о наличие во временном ряде расходов на конечное потребление сильной линейной тенденции.

Аналогично можно определить коэффициенты второго и более высоких порядков. Так, коэффициент автокорреляции второго порядка характеризует тесноту связи между уровнями ряда у _t и у _t-2, и определяется по формуле:

,

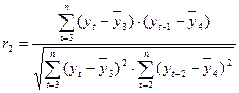где

; .

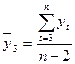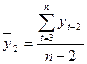Число периодов, по которым рассчитываются коэффициент автокорреляции, называется лагом. С увеличением лага число пар значений, по которым рассчитывается коэффициент автокорреляции, уменьшается.

Свойства коэффициента автокорреляции:

- так как он строится по аналогии с линейным коэффициентом корреляции, то он характеризует тесноту только линейной связи текущего и предыдущего уровней связи; по данному коэффициенту можно судить о наличии линейной тенденции; для некоторых временных рядов, имеющих сильную нелинейную тенденцию коэффициент может приближаться к нулю;

- по знаку коэффициента автокорреляции сделать вывод о тенденции ряда невозможно.

Последовательность коэффициентов автокорреляции уровней первого, второго и т.д. порядков называют автокорреляционной функцией временного ряда. График зависимости ее значений от величины лага называется коррелограммой.

Рассчитав несколько коэффициентов автокорреляции можно определить лаг, при котором автокорреляция наиболее высока, выявив тем самым структуру временного ряда. Если наиболее высоким оказывается значение 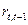, то исследуемый ряд содержит тенденцию; если наиболее высоким оказался 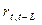, то ряд содержит циклические колебания с периодом L. Если ни один из коэффициентом не является значимым, можно сделать одно из двух предположений:

- либо ряд не содержит тенденции и циклических колебаний, а его уровень определяется только случайной компонентой;

- либо ряд содержит сильную нелинейную тенденцию.

Построение аналитической функции для моделирования тенденции (тренда) временного ряда называют аналитическим выравниванием временного ряда. Для этого чаще всего применяются следующие функции:

· линейная ;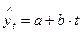

· гипербола ;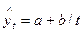

· экспонента ;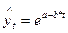

· степенная функция ;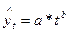

· парабола второго и более высоких порядков .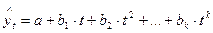

Параметры трендов определяются МНК, в качестве независимой переменной выступает время, а в качестве зависимой переменной – фактические уровни временного ряда. Для нелинейных трендов предварительно проводят стандартную процедуру их линеаризации.

Критерием отбора наилучшей формы тренда является наибольшее значение скорректированного коэффициента детерминации.

Пример. Определим МНК параметры линейного тренда на основе данных табл. 4.3.

Таблица 4.3

Дата добавления: 2014-01-03