Расстояние между объектами и мера близости

Наиболее трудным и наименее формализованным в задаче классификация является определение понятия однородности объектов.

В общем случае понятие однородности объектов задается либо введением правила вычислений расстояния 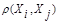между любой парой исследуемых объектов (Х₁,Х₂,..,Х_n), либо заданий некоторой функций, характеризующей степень близости i-го и j-го объектов. Если задана функция 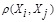, то близкие с точки зрения этой метрики объекты считаются однородными, принадлежащие одному классу. При этом необходимо сопоставлять 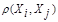с некоторым пороговым значением, определенным в каждом конкретном случае по-своему.

Аналогично используются и мера близости 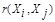, при задании которой надо помнить о необходимости выполнения условий симметрии 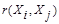=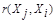; максимального сходства объекта с самим собо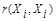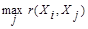й при 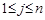, и монотонного убывания 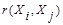по 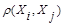, т.е. из ≥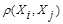должно следовать неравенство ≤.

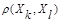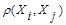Выбор метрики или меры близости является узловым моментом исследования, от которого в основном зависит окончательный вариант разбиения объектов на классы при данном алгоритме разбиения. В каждом конкретном случае этот выбор должен производиться по – своему в зависимости от целей исследования, физической и статистической природы вектора наблюдений X, априорных сведений о характере вероятностного распределения Х.

Рассмотрим наиболее часто используемые расстояния и меры близости в задачах кластерного анализа.

Расстояние махаланобиса (общий вид)

В случае зависимости компонент 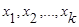вектора наблюдений Х и их различной значимости в решении вопроса квалификации обычно используют обобщенное (взвешенное) расстояние Махаланобиса, задаваемое формулой

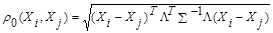, (7.1)

где 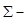ковариационная матрица генеральной совокупности, из которой извлекаются наблюдения;

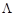- некоторая симметрическая неотрицательно-определенная матрица «весовых» коэффициентов, которая чаще всего выбирается диагональной.

Следующие три вида расстояний являются частными случаями метрики ρ_0.

ОБЫЧНОЕ ЭВКЛИДОВОЕ РАССТОЯНИЕ

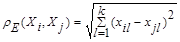( 7.2)

где 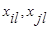- величина l- й компоненты у i -го (j -го) объекта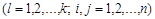

Использование этого расстояния оправдано в случаях, если:

а) наблюдения берутся из генеральных совокупностей, имеющих многомерное нормальное распределение с ковариационной матрицей вида , т.е компоненты Х взаимно независимы и имеют одну и ту же дисперсию;

б) Компоненты вектора наблюдения Х однородны по физическому смыслу и одинаковы важны для классификации;

в) признаковое пространство совпадает с геометрическим пространством.

Естественно с геометрической точки зрения и содержательной интерпретации евклидовое расстояние может оказаться бессмысленным, если его признаки имеют разные единицы измерения. Для приведения признаков к одинаковым единицам прибегают к нормировке каждого признака путем деления центрированной величины на среднее квадратическое отклонение и переходят от матрицы Х к нормированной матрице с элементами

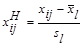
где 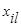- значение l- го признака i -го объекта;

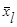- среднее арифметическое значение l- го признака;

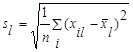- среднеквадратическое отклонение l- го признака;

Однако это операция может привести к нежелательным последствиям. Если кластеры хорошо разделены по одному признаку и не разделены по другому, то после нормировки дискриминирующие возможности первого признака будут уменьшены в связи с увеличением «шумового» эффекта второго.

«ВЗЕШЕННОЕ» ЕВКЛИДОВО РАССТОЯНИЕ

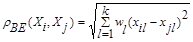(7.3)

применяется в случаях, когда каждой компоненте 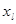вектора наблюдений Х удается приписать некоторый «вес» w_l, пропорциональной степени важности признака задачи классификации. Обычно принимают 0≤ wt≤1 где l=1, 2,…,k.

Определение «весов», как правило, связано с дополнительными исследованиями, например, организацией опроса экспертов и обработкой их мнений. Определение весов w_l только по данным выборки может привести к ложным выводам.

Дата добавления: 2014-01-03