Функционалы качества разбиения

Существует большое количество различных способов разбиения на классы заданной совокупности элементов. Поэтому представляет интерес задача сравнительного анализа качества этих способов разбиения. С этой целью вводится понятие функционала качества разбиения Q (S), определенного на множество всех возможных разбиений.

Наилучшее разбиение S* представляет собой такое разбиение, при котором достигается экстремум выбранного функционала качества. Следует отметить, что выбор такого или иного функционала качества разбиения, как правило, опирается на эмпирическое соображения.

Рассмотрим некоторое наиболее распространенные функционалы качества разбиения. Пусть исследованием выбрана метрика 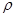в пространстве X и S=(S₁,S₂,…,S_p) некоторое фиксированное разбиение наблюдений X₁, X₂,…,X_n на заданное число 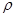классов S₁,S₂,…,S_P.

Существуют следующие характеристики функционала качества:

─ сумма внутриклассовых дисперсий

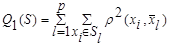; (7.12)

─ сумма попарных внутриклассовых расстояний между элементами

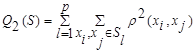(7.13)

или

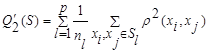
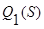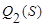, широко используются в задачах кластерного анализа для сравнения качества процедур разбиения;

─ обобщенная внутриклассовая дисперсия

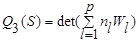(7.14)

где det A - определитель матрицы А;

W_l = выборочная ковариационная матрица класса S_l, элементы которой определяются по формуле

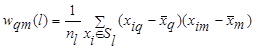где q,m=1,2,…,k,

где 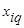-q-я компонента многомерного наблюдения x_i;

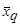- среднее значение q-й компоненты, вычисленное по наблюдениям l-го класса.

Качество разбиения характеризуют и другим видом обобщенной дисперсии, в которой операция суммирования W_i заменена операцией умножения

.

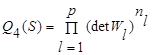Отметим, что функционалы 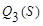, 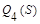обычно используют при решении вопроса: не сосредоточены ли наблюдения, разбитые на классы, в пространстве размерности, меньшей, чем k.

Дата добавления: 2014-01-03