Расстояние между кластерами

В ряде процедур классификации (кластер-процедур) используют понятия расстояния между группами объектов и меры близости двух групп объектов.

Пусть S_i - i- я группа (класс, кластер), состоящая из n_i объектов;

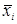- среднее арифметическое векторных наблюдений S_i группы, т.е. «центр тяжести» i- ой группы;

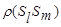-расстояние между группами S_l и S_m..

Наиболее употребительными расстояниями и мерами близости между объектов являются:

─ расстояние, измеряемое по принципу «ближайшего соседа»

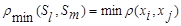(7.5)

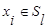
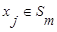
─ расстояние, измеряемое по принципу «дальнего соседа»

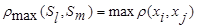(7.6)

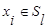
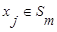
─ расстояние, измеряемое по «центрам тяжести» групп

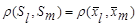(7.7)

─ расстояние, измеряемое по принципу «средней связи». Это расстояние определяется как среднее арифметическое всех парных расстояний между представителями рассматриваемых групп

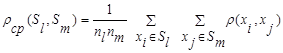(7.8)

Академиком А.Н.Колмогоровым было предположено «обобщенное расстояние» между классами, которое в качестве частных случаев включает в себя все рассмотренные выше виды расстояний.

Обобщенное расстояние основано на понятии так называемого «обобщенного среднего», а точнее – степенного среднего и определяется формулой:

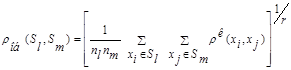(7.9)

Можно показать, что при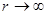

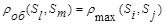
при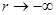

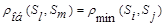
при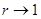

.

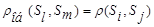Из формулы (7.9) следует, что если 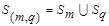-группа элементов, полученная путем объединения кластеров 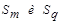, то обобщенное расстояние между кластерам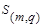и и 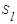определяется по формуле

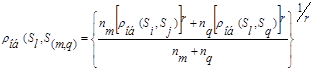(7.10)

Расстояние между группами элементов особенно важно в так называемых агломеративных иерархических кластер – процедурах, так как принцип работы таких алгоритмов состоит в последовательном объединении сначала самых близких элементов, а затем и целых групп все более и более отдаленных друг от друга элементов.

При этом расстояние между классам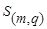и и 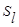, являющимся объединением двух других классов 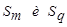, можно определить по формуле:

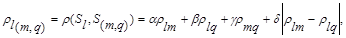(7.11)

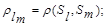
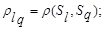
где 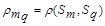- расстояние между классами ;

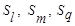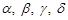-числовые коэффициенты, значение которых определяет специфику процедуры, ее алгоритм.

Например, пр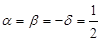и и 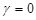приходим к расстоянию, построенному по принципу «ближайшего соседа». Пр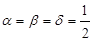и и 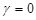расстояние между классами определяется по принципу «дальнего соседа», как расстояние между двумя самыми дальними элементами этих классов. И наконец, при

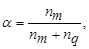
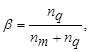
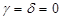
Соотношение (7.11) приводит к расстоянию ρ между классами, вычисленному как среднее из расстояния между всеми парами элементов, один из которых берется из одного класса, а другой – из другого класса.

Дата добавления: 2014-01-03