Решение. Провести классификацию n=6 объектов, каждый из которых характеризуется двумя признаками

Пример 7.1

Провести классификацию n=6 объектов, каждый из которых характеризуется двумя признаками.

№ объекта i
xi1 xi2

Расположение объектов в виде точек на плоскости показано на рисунке

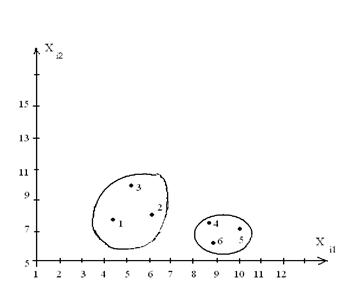
Рис. 7.1. Классификация объектов.

Воспользуемся алгомеративным иерархическим алгоритмом классификации. В качестве расстояниями между объектами возьмем обычное евклидово расстояние. Тогда согласно формуле (7.2) расстояние между первым и вторым объектом

,

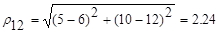а между первым и третьим объектами

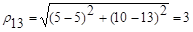
Очевидно, что

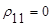
Аналогично находим расстояние между шестью объектами и строим матрицу расстояний.

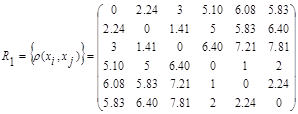
Из матрицы расстояний следует, что четвертый и пятый объекты наиболее близки 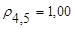и поэтому объединяютcя в один кластер.

После объединения объектов имеем пять кластеров:

Номер кластера
Состав кластера	(1)	(2)	(3)	(4,5)	(6)

Расстояние между кластерами определим по принципу «ближайшего соседа», воспользовавшись формулой пересчета (7.11). Так расстояние между объектом S₁ и кластером S_(4,5)

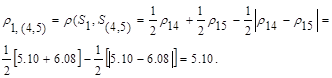
Таким образом, расстояние 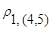равно расстоянию от объекта 1 до ближайшего к нему объекта, входящего в кластер 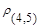, т.е. 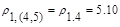. Тогда матрица расстояний

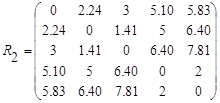
Объединим второй и третий объекты, имеющие наименьшее расстояние 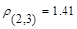. После объединения объектов имеем четыре кластера:

S₍₁₎ , S_(2.3) , S_(4.5) , S_(6).

Вновь найдем матрицу расстояний. Для того чтобы рассчитать расстояние до кластера S_(2.3) воспользуемся матрицей расстояний R₂. Например, расстояние между кластерами S_(4.5) и S_(2.3) равно

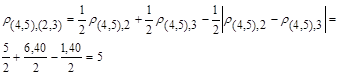
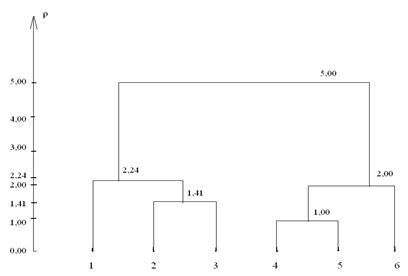Рис. 7.2 Дендрограмма

Проведя аналогичные расчеты, получим

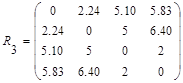
Объединим кластеры S_(4.5) и S₍₆₎, расстояние между которыми, согласно матрице R₃, наименьшее 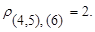В результате получим три кластера

S₍₁₎ , S_(2,3) , S_(4.5,6).

Матрица расстояний будет иметь вид:

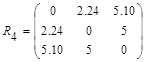
Объединим теперь кластеры S₍₁₎ , S_{(2,3) ,} расстояние между которыми 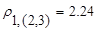. В результате получим два кластера S_(1,2,3) и S_(4.5,6), расстояние между которыми, найденное по принципу «ближайшего соседа»,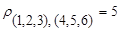

Результаты иерархической классификации объектов представлены на рис. 7.2. в виде дендограммы.

На рис. 7.2 приводится расстояние между объединяемыми на данном этапе кластерами (объектами). В нашем примере предпочтение следует отдать предпоследнему этапу классификации, когда все объекты объединены в два кластера (рис.7.2)

S_(1,2,3) и S_(4.5,6)

Дата добавления: 2014-01-03