Момент сили

Для характеристики зовнішньої механічної дії на тіло, яка приводить до зміни обертального руху тіла, вводять поняття моменту сили. Розрізняють момент сили відносно точки та осі обертання.

Момент сили 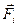відносно нерухомої т.О ( центр обертання) – це ФВ, яка визначається векторним добутком радіус-вектора 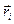, проведеного із т.О в т. m_i прикладання сили, на силу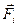

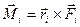(13)

Модуль моменту сили

М_i=F_i r_i sin α (14)

α – кут між 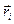і 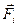, l – найкоротша відстань між лінією дії сили і т. О – плече сили. 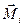- - псевдовектор або аксіальний вектор, його напрям співпадає з напрямом поступального руху правого гвинта при його обертанні від 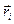до 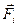(рис.5.2.) або за правилом векторного добутку.

Момент сили характеризує здатність сили обертати тіло навколо точки, відносно якої він береться.

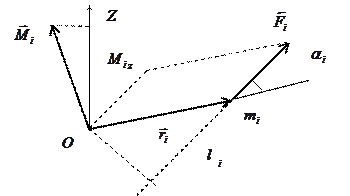
Рис.5.2

Момент сили 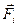відносно нерухомої осі O Z називається скалярна величина 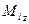рівна проекції на цю вісь вектора 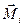момента сили, визначеного відносно довільної точки О даної осі Z. Значення 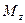не залежить від вибору положення т.О на осі Z. Розмірність в СІ 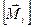=1 Н·м.

Векторна сума моментів 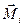всіх зовнішніх сил, які прикладені до тіла називається головним моментом зовнішніх сил відносно т. О.

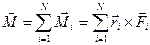(15)

Головний момент (результуючий момент) відносно нерухомої осі ОZ системи

характеризує здатність сили обертати систему (тіло) навколо цієї осі та дорівнює алгебраїчній сумі моментів всіх сил системи відносно цієї осі

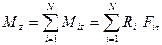(16)

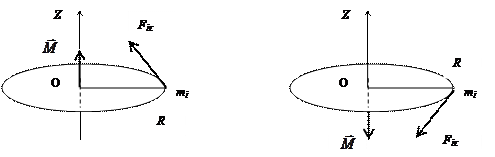а) б)

Рис.5.3

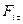- тангенціальна (дотична) складова сили 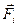, саме ця складова викликає обертання навколо осі Z, R – радіус кола.

У техніці машин і механізмів момент сили часто називають крутильним моментом.

Основне рівняння динаміки обертального руху ТТ

Існують такі осі обертання тіл, які не змінюють своєї орієнтції без дії на них зовнішніх сил. Такі осі називаються вільними або осями вільного обертання. В будь-якому тілі існують три взаємно перпендикулярні осі, які проходять через центр мас тіла, котрі можуть бути вільними осями. Їх називають головними осями інерції. Наприклад, головні осі інерції однoрідного прямокутного паралелепіпеда проходять через центри протилежних граней рис.6.1. Обертання найстійкіше навколо осі з найбільшим моментом інерції. Найлегше відбувається обертання навколо осі з найменшим моментом інерції.

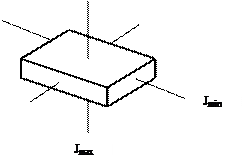Рис.6.1

Якщо вісь обертання ТТ співпадає з головною віссю інерції, яка проходить через центр мас, має місце векторна рівність

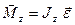(17)

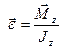(18)

Кутове прискорення ТТ, яке обертається навколо нерухомої осі ОZ, прямо пропорційне результуючому моменту відносно цієї осі всіх зовнішніх сил, що діють на тіло і обернено пропорційне моменту інерції тіла відносно тієї ж осі.

Рівняння (14), (15) називають рівнянням динаміки обертального руху ТТ.

Примітка.

У рівняннях (17) і (18) індекс Z означає не проекцію 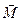на вісь Z, а те що обертання ТТ і момент інерції розглядаються відносно осі Z/

Закон збереження моменту імпульсу тіла.

Аналогічно тому, як поступальний рух МТ (тіла) характеризується імпульсом тіла, так в обертальному русі є характеристика, яка називається моментом імпульсу МТ (тіла).

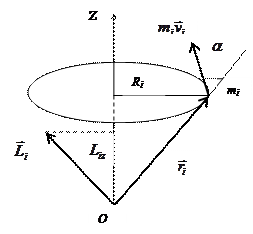Моментом імпульсу (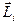) МТ відносно нерухомої т. О називається векторна ФВ рівна векторному добутку радіус-вектора 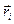МТ, який проведений із т.О в т. 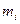на імпульс цієї МТ 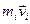, рис.1. Його наgрям визначається правилом векторного добутку/

Рис.7.1

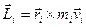(19)

Модуль моменту імпульса

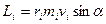( 20 )

Моментом імпульсу МТ відносно нерухомої осі Z називається скалярна величина 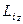, яка дорівнює проекції на цю вісь 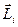вектора моменту імпульса відносно довільної т. О на осі Z.

Момент імпульсу ТТ відносно т.Оє векторна величина рівна векторній сумі моментів імпульса 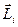всіх МТ ТТ

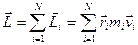(21)

Момент імпульсу ТТ відносно нерухомої осі Z називається скалярна величина 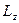, яка дорівнює проекції на цю вісь 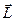вектора моменту імпульса відносно довільної т. О на осі Z.

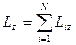(22)

Значення моменту імпульса 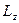не залежить від положення т. О на осі Z.

Закон збереження моменту імпульсу тіла.

Розглянемо обертальний рух МТ, яка рухається по колу радіусом R_i рис.7.1. Тоді

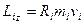
для ТТ момент імпульса відносно осі Z виразиться

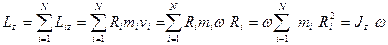
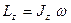(23)

Отримали вираз для моменту інерціїї ТТ відносно осі Z через кутову швидкість обертання. Візьмемо першу похідну від виразу (20) за часом, тоді

.

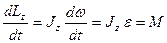У загальному вигляді матимемо

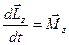(24)

Це є основний закон динаміки обертального руху ТТ (аналогічний по запису для поступального руху ТТ 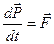). Формулювання основного закону динаміки обертального руху ТТ: швидкість зміни моменту імпульсу дорівнює моменту обертальної сили (якщо діє кілька моментів сил, то результуючому моменту)

Рівняння (21) називають ще рівнянням моментів: похідна по часу від моменту імпульсу МТ відносно нерухомого початку (полюса) дорівнює моменту рушійноїсили, що діє відносно того ж полюсу.

Із (21) випливає дуже важливий закон збереження моменту імпульсу: при відсутності моменту зовнішніх сил момент імпульс є величиною постійною. Дійсно, якщо 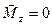, то

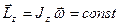(25)

Згідно (22) можна під дією лише внутрішніх сил системи, змінюючи момент інерції, змінити кутову швидкість обертання ТТ.

Завдання на СРС

1.Таблиця 2. Співставлення основних характеристик поступального і обертального рухів

2. Реактивний рух. Рівняння Мещерського.

Рух деяких тіл супроводжується зміною їх маси. Наприклад, маса ракети зменшується при згоранні пального. Виведемо рівняння руху тіла змінної маси. Якщо в момент часу t маса ракети m, а її швидкість v, то за наступний проміжок часу dt її маса зменшиться на dm і стане рівною m- dm,а швидкість v+dv. Зміна імпульсу системи за час dt буде

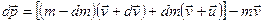
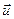- швидкість витікання газів відносно ракети.. В результаті отримаємо

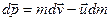
якщо на систему діють зовнішні сили, то 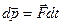і тому

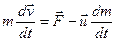
Член 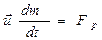називають реактивною силою. Якщо 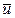протилежна 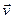, то ракета прискорюється, а якщо співпадає. то гальмується. Т.ч. отримали рівняння руху тіла із змінною масою

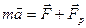(26)

Це рівняння вперше виведене І.В.Мещерським і носить його ім’я.

Якщо 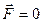, то

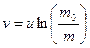(27)

чим більша швидкість витікання газів, тим більша може бути кінцева маса при даній стартовій масі ракети

Це формула Ціолковського, фундатора космонавтики.

Лекція 3. Робота. Енергія. Потужність

Предметом вивчення природних наук є форми руху матерії. З досліду відомо, що рух може переходити з однієї форми в іншу, але він не знищувальний, оскільки сама матерія знаходиться в безперервному русі. Мірою руху матерії є фізична величина, яка називається енергією.

Як показують експерименти при переході руху з однієї форми в іншу зменшення енергії пов'язане з рухом однієї форми і рівне приросту енергії, пов'язаного з рухом іншої форми. Кількість енергії, яка перейшла з однієї форми в іншу дорівнює різниці енергії до переходу і після переходу. Різниця цих енергій, тобто кількість енергій яка перейшла з однієї форми в іншу називається роботою.

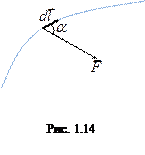В механіці під роботою сили 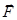, під дією якої тіло здійснює переміщення 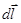(рис. 1.14) називається фізична величина, яка визначається із співвідношення:

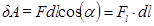, (1.68)

де α — кут між векторами 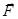і 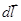, 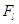- проекція вектора 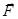на переміщення .

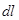Виходячи з поняття скалярного добутку, роботу можна визначити за формулою:

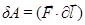(1.69)

У випадку якщо тіло рухається по кривій (по криволінійній траєкторії), то для того, щоб знайти роботу сили, що діє на тіло при переміщенні його між двома точками, потрібно цю траєкторію розбити на достатньо малі ділянки, такі, щоб їх можна було вважати прямолінійними, а силу на цих ділянках сталою, знайти роботу на кожній з цих ділянок і результати скласти.

На графіку залежності сили F від переміщення l робота буде рівна площі криволінійної трапеції (рис. 1.15). В загальному випадку роботу тіла при переміщенні тіла з т.1 в т.2 знаходять із співвідношення:

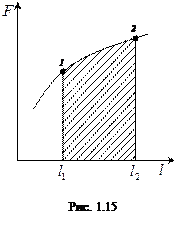
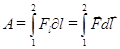(1.68)

Якщо на тіло діє не одна, а декілька сил, то тоді рівнодійна:

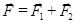(1.69)

і тоді: ,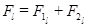

а робота:

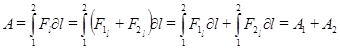. (1.70)

Робота, виконана декількома силами, що діють на дане тіло дорівнює алгебраїчній сумі робіт виконаних кожною силою окремо. В СІ одиницею роботи є 1 Дж = 1 Н ∙ 1 м

Величина

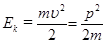(1.71)

називається кінетичною енергією тіла, а співвідношення:

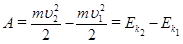(1.72)

називається теоремою про кінетичну енергію: робота сили при переміщенні матеріальної точки дорівнює приросту кінетичної енергії цієї точки.

Робота, виконана силою гравітаційного тяжіння, не залежить від форми траєкторії, по якій рухається тіло, а визначається тільки початковим і кінцевим положенням тіла. Сили, робота яких не залежить від форми траєкторії по якій рухається тіло, називаються консервативними. Якщо залежить, то неконсервативними. А поля, в яких діють консервативні сили – потенціальними. Робота консервативних сил по замкнутому контуру рівна нулю. Це є математичний критерій потенціальності поля консервативних сил:

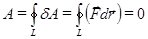(1.73)

Тобто, циркуляція вектора сили 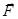по довільному замкненому контуру L дорівнює нулю.

Потенціальна енергія – це функція стану величини, яка визначається тільки положенням, диференціал цієї величини дорівнює елементарній роботі з протилежним знаком.

Потенціальна енергія тіла в полі земного тяжіння:

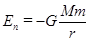(1.74)

Потенціальна енергія тіла, піднятого на висоту h над нульовим рівнем:

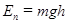(1.75)

Потенціальна енергія стягнутої (розтягнутої) пружини:

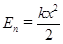(1.76)

Робота при обертальному русі.

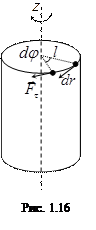
Нехай до абсолютно твердого тіла прикладено дотичну силу 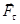, під дією якої воно повернулось на малий кут 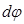(рис. 1.16). При цьому точка прикладання сили перемісти- ться на відстань 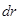. Переміщення 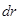можна визначити через

радіус R та кут :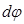

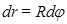(1.77)

З рисунка 1.16 видно, що l — плече сили 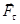. Елементарна робота:

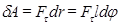(1.78)

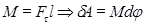, (1.79)

тобто елементарна робота при повороті тіла на елементарний кут 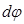чисельно дорівнює добутку моменту діючої сили на цей кут. Якщо тіло повернулось на певний кут 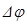від положення 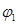до положення 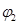, то повна робота в обертальному русі:

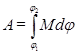(1.80)

Якщо М =const, то:

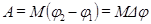(1.81)

Закони збереження енергії в механіці

Якщо у механічній системі діють сили тертя або опору, механічна енергія поступово зменшується за рахунок перетворення в інші види енергії (наприклад у теплову). Цей процес називається дисипацією (розсіюванням) енергії.

Механічна енергія не зберігається, а виконується загальнофізичний закон збереження енергії:

Енергія не виникає з нічого і не зникає безслідно: вона може тільки передаватись від одних фізичних систем до інших або переходити з одного виду в інший в еквівалентних кількостях.

Якщо ж в системі сили тертя не діють або ж вони настільки малі, що ними нехтують, то виконується закон збереження механічної енергії:

У замкненій системі консервативних сил повна механічна енергія є величиною сталою:

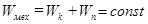- для матеріальної точки (1.82)

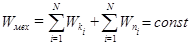- для системи матеріальних точок (1.83)

Потужність

Одну і ту ж роботу різні сили виконують за різний час. Робота, що виконується за одиницю часу називається потужність або миттєва потужність. Потужність визначається із співвідношення:

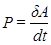(1.84)

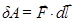; (1.85)

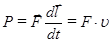(1.86)

В СІ одиницею потужності є 1 Вт = 1 Дж/1с.

Середня потужність — фізична величина, що визначається відношенням всієї виконаної роботи А до часу Δt, за який цю роботу було виконано:

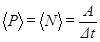(1.87)

При обертальному русі матеріальної точки (абсолютно твердого тіла):

,

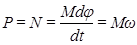де M — момент діючої сили, ω — миттєва кутова швидкість матеріальної точки (абсолютно твердого тіла).

ЛЕКЦІЯ 04

Дата добавления: 2014-01-03