
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Феромагнетики
|
|
|
|
Феромагнетики – це тверді (як правило, кристалічні) речовини, такі як залізо, кобальт, нікель, деякі рідкоземельня метали, ряд сплавів, які при не дуже високих температурах мають мимовільну (спонтанну) намагніченість, яка сильно змінюється під впливом зовнішнього магнітного поля, деформації, змінювання температури тощо. На відміну від слабо магнітних діа- і парамагнетиків внутрішнє магнітне поле в них може в сотні і тисячі раз перевершувати зовнішнє поле.
Основні магнітні властивості феромагнетиків. такі:
а) Нелінійна залежність намагніченості J від напруженості H магнітного поля (рис. 11.2), При H > Н н спостерігається магнітне насичення, тобто J = J н = const незалежно від значення Н н (на відміну від парамагнетиків, значення Н н, при якому наступає магнітне насичення, порівняно невелике).
б) При Н < Н н залежність магнітної індукції В від напруженості H нелінійна, а при Н > Н н вона стає лінійною (рис. 11.3).
в) Залежність відносної магнітної проникності 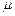 від напруженості H має складний характер (рис. 11.4), причому максимальні значення
від напруженості H має складний характер (рис. 11.4), причому максимальні значення 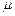 дуже великі:
дуже великі: 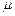 макс = 103 ÷106.
макс = 103 ÷106.
г) Існування магнітного гістерезису – відмінності в значеннях намагніченості J феромагнетика при одному і тому ж самому значенні H напруженості намагнічуваного поля залежно від значення попередньої намагніченості феромагнетика (рис. 11.5).

Рис. 11.2 Рис. 11.3
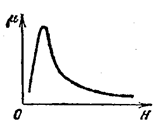
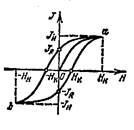
Рис. 11.4 Рис. 11.5
д) У кожної феромагнітної речовини є така температура, яка називається точкою Кюрі, вище за яку ця речовина втрачає свої особливі магнітні властивості і поводиться як звичайний парамагнетик.
Петля гістерезису – це показаний на рис. 11.5 графік залежності намагніченості феромагнетика від напруженості магнітного поля при змінюванні напруженості від Н н до – Н н і навпаки, де Н н – напруженість поля, що відповідає магнітному насиченню (рис. 11.5). Намагніченість J н при Н = Н н називається намагніченістю насичення. Намагніченість ± JR при Н = 0 називається залишковою намагніченістю. Існування залишкової намагніченості у феромагнетика, видаленого з магнітного поля, служить основою для створення постійних магнітів.
Напруженість ± Н к магнітного поля, яке повністю розмагнічує феромагнітний зразок, називається коерцитивною силою (затримуючою напруженістю). Коерцитивная сила характеризує здатність феромагнетика зберігати намагнічений стан. Велику коерцитивну силу (широку петлю гістерезису) мають магнітотверді матеріали, що використовуються для виготовлення постійних магнітів. Малу коерцитивну силу (відповідно вузьку петлю гістерезису) мають магнітом'які матеріали, що використовуються для виготовлення магнітних кіл (осердь) трансформаторів.
Періодичне перемагнічування феромагнітного зразка пов'язано з витратою енергії на його нагрівання. Площа петлі гістерезису пропорційна кількості теплоти, що виділяється в одиниці об'єму феромагнетика за один цикл перемагнічування.
За температурах нижче за точку Кюрі феромагнітний зразок розбивається на малі області, мимовільної (спонтанної) однорідної намагніченості, які називаються доменами. Лінійні розміри доменів порядку (10-5 ÷ 10-4 м). Усередині кожного домена речовина намагнічена до насичення. За відсутності зовнішнього магнітного поля магнітні моменти доменів орієнтовані в просторі так, що результуючий магнітний момент зразка дорівнює нулю і феромагнетик не намагнічений.
Намагнічення феромагнітного зразка в зовнішньому магнітному полі полягає, по-перше, в зсуві границь доменів і зростанні розмірів тих доменів, вектори магнітних моментів яких близькі у напрямку до магнітної індукції В поля, і, по-друге, в повороті магнітних моментів цілих доменів по напряму поля В. В достатньо сильному магнітному полі досягається стан магнітного насичення, коли весь зразок намагнічений по полю і його намагніченість J не змінюється при подальшому збільшенні В.
Вимірювання гіромагнітного відношення для феромагнетиків показали, що елементарними носіями магнетизму в них є магнітні моменти спінів електронів.
ЛЕКЦІЯ 12
Електромагнітна індукція
1. Явище електромагнітної індукції. Закон Фарадея. Правило Ленца
Досліди Фарадея і наслідки з них.
Дослід I (рис. 12.1). Якщо в замкнений на гальванометр соленоїд всувати або висувати постійний магніт, то в моменти його всування або висування спостерігається відхилення стрілки гальванометра (виникає індукційний струм); напрями відхилення стрілки при всуванні і висовуванні магніта протилежні. Відхилення стрілки гальванометра тим більше, чим більше швидкість руху магніта відносно котушки. У разі змінювання полюсів магніта напрям відхилення стрілки зміниться. Для отримання індукційного струму магніт можна залишати нерухомим, тоді потрібно пересувати соленоїд відносно магніта.
Дослід II. Кінці однієї з котушок, вставлених одна в другу, приєднуються до гальванометра, а через іншу котушку пропускається струм. Відхилення стрілки гальванометра спостерігається в моменти ввімкнення або вимкнення струму, в моменти його збільшення або зменшення або у разі переміщування котушок одна відносно одної (рис. 12.2). Напрями відхилень стрілки гальванометра також протилежні у разі ввімкнення і вимкнення струму, його збільшення і зменшення, зближення і видалення котушок.
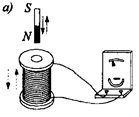
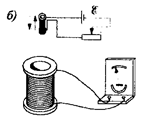
Рис. 12.1 Рис. 12.2
Висновки:
1. Індукційний струм виникає завжди, коли відбувається змінювання зчепленого з контуром потоку магнітної індукції.
2. Сила індукційного струму абсолютно не залежить від способу змінювання потоку магнітної індукції, а визначається лише швидкістю його змінювання.
Електромагнітна індукція – це явище, яке полягає в тому, що в замкненому контурі у разі змінювання потоку магнітної індукції, що охоплюється цим контуром, виникає струм, який називають індукційним струмом.
Закон Фарадея. Узагальнюючи результати дослідів, М. Фарадей показав, що всякий раз, коли відбувається змінювання зчепленого з контуром потоку магнітної індукції, в контурі виникає індукційний струм; виникнення індукційного струму вказує на наявність в електричному колі е.р.с., яка називається е.р.с. електромагнітної індукції.
Закон Фарадея формулюється так: е.р.с. електромагнітної індукції чисельно дорівнює і протилежна за знаком швидкості змінювання магнітного потоку через поверхню, обмежену цим контуром:
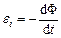 .
.
Закон Фарадея можна вивести з закону збереження енергії. Для цього слід розглянути провідник з струмом 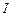 , який вміщено в однорідне магнітне поле, перпендикулярне площині контуру і який може переміщуватись. Згідно з законом збереження енергії робота джерела струму за час
, який вміщено в однорідне магнітне поле, перпендикулярне площині контуру і який може переміщуватись. Згідно з законом збереження енергії робота джерела струму за час 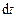 складається з роботи на джоулеве тепло і роботи по переміщенню провідника в магнітному полі:
складається з роботи на джоулеве тепло і роботи по переміщенню провідника в магнітному полі:
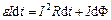 ,
,
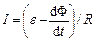
де – 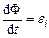 – закон Фарадея.
– закон Фарадея.
Встановимо розмірність 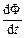 .
.
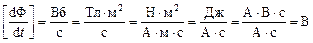 .
.
Правило Ленца. В законі Фарадея 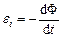 знак мінус показує, що збільшення магнітного потоку викликає
знак мінус показує, що збільшення магнітного потоку викликає 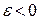 (тобто поле індукованого струму спрямовано назустріч потоку), зменшення потоку викликає
(тобто поле індукованого струму спрямовано назустріч потоку), зменшення потоку викликає 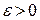 (тобто напрям потоку і поля індукованого струму співпадають). Знак мінус в законі Фарадея – це і є математичний вираз правила Ленца – загального правила для знаходження напрямку індукованого струму.
(тобто напрям потоку і поля індукованого струму співпадають). Знак мінус в законі Фарадея – це і є математичний вираз правила Ленца – загального правила для знаходження напрямку індукованого струму.
Формулювання правила Ленца таке: індукційний струм в контурі завжди має такий напрям, що створюване ним магнітне поле заважає змінюванню магнітного потоку, який викликав цей індукційний струм.
2. Взаємоіндукція.Взаємна індуктивність двох котушок на спільному осерді.
Розглянемо два контури 1 і 2 з струмами 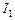 і
і 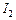 , які розташовані близько один до одного ( рис. 14.4 ). У разі протікання в контурі 1 струму
, які розташовані близько один до одного ( рис. 14.4 ). У разі протікання в контурі 1 струму 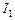 магнітний потік (суцільні лінії на рисунку) пронизує контур 2:
магнітний потік (суцільні лінії на рисунку) пронизує контур 2:
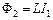 .
.
Аналогічно
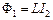 .
.
Коефіцієнти пропорційності 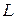 , які називаються взаємною індуктивністю контурів, виявились однаковими.
, які називаються взаємною індуктивністю контурів, виявились однаковими.
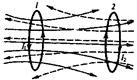
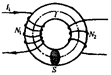
Рис. 12.3 Рис. 12.4
У разі змінювання сили струму в одному з контурів, в другому індукується е.р.с. згідно з законом Фарадея
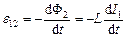 ;
;
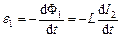 .
.
Взаємна індукція – це явище виникнення е.р.с. в одному з контурів у разі змінювання сили струму в другому контурі.
Взаємна індуктивність контурів залежить від геометричної форми, розмірів, взаємного розташування контурів, а також від магнітної проникності оточуючого середовища.
Взаємна індуктивність двох котушок на спільному осерді. Розглянемо дві котушки на спільному осерді ( рис. 12.5 ). Магнітна індукція поля, створюваного першою котушкою з числом витків 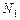 , струмом
, струмом 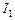 и магнітною проникністю
и магнітною проникністю 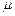 осердя, дорівнюватиме
осердя, дорівнюватиме
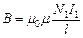 ,
,
де 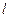 довжина осердя по середній лінії.
довжина осердя по середній лінії.
Магнітний потік крізь один виток другої котушки
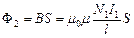 .
.
Тоді повний магнітний потік (потокозчеплення) крізь 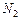 витків вторинної обмотки
витків вторинної обмотки
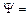
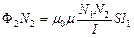 .
.
Поток 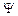 створюється струмом
створюється струмом 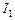 , тому (оскільки частина потоку, що пронизує витки вторинної обмотки
, тому (оскільки частина потоку, що пронизує витки вторинної обмотки 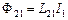 )
)
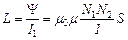 .
.
3. Індуктивність контуру. Самоіндукція. Е. р. с. самоіндукції
Індуктивність контуру. Магнітна індукція 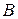 поля, створюваного струмом, по закону Біо-Савара-Лапласа пропорційна силі струму
поля, створюваного струмом, по закону Біо-Савара-Лапласа пропорційна силі струму 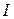 . Саме тому зчеплений з контуром магнітний потік пропорційний струму в контурі:
. Саме тому зчеплений з контуром магнітний потік пропорційний струму в контурі:
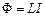 ,
,
де коефіцієнт пропорційності 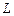 називається індуктивністю контуру.
називається індуктивністю контуру.
Індуктивність контуру в загальному випадку залежить лише від геометричної форми контуру, його розмірів і магнітної проникності того середовища, в якому він знаходиться.
Одиниця індуктивності – Гн. 1 Гн (генрі – це індуктивність такого контуру, магнітний потік самоіндукції якого у разі протікання по ньому струму в 1 А дорівнює 1 Вт:
1 Гн = 1 Вб/А = 1 В·с/А.
Е.р.с. індукції в нерухомих провідниках.
Згідно з законом Фарадея виникнення е.р.с. електромагнітної індукції можливе також у випадку нерухомого контуру, який знаходиться в змінному магнітному полі. Згідно з трактовкою Максвелла: всяке змінне магнітне поле збуджує в оточуючому просторі електричне поле, яке і є причиною виникнення індукційного струму в нерухомому провіднику. Циркуляція 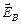 цього поля по будь-якому нерухомому контуру
цього поля по будь-якому нерухомому контуру 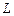 провідника є е.р.с. електромагнітної індукції
провідника є е.р.с. електромагнітної індукції
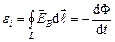 .
.
Самоіндукція
Застосовуючи до самоіндукції закон Фарадея у випадку змінювання в провідному контурі сили струму, матимемо залежність:
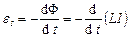 .
.
У випадку, коли контур не деформується і магнітна проникність середовища не змінюється, то 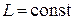 і, отже,
і, отже,
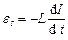 ,
,
де знак мінус, обумовлений правилом Ленца, показує, що наявність в контурі індуктивності викликає в ньому уповільнення змінювання струму. Так, у разі зростання струму 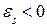 , тобто струм самоіндукції направлений назустріч струму, обумовленому зовнішнім джерелом, і гальмує його збільшення.
, тобто струм самоіндукції направлений назустріч струму, обумовленому зовнішнім джерелом, і гальмує його збільшення.
Індуктивність нескінченно довгого соленоїда. Соленоїд – це згорнутий в спіраль ізольований провідник, по якому протікає електричний струм. Повний магнітний потік соленоїда (потокозчеплення)
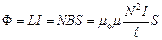 .
.
Отже
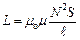 ,
,
де 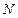 – число витків соленоїда;
– число витків соленоїда; 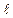 – його довжина;
– його довжина; 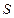 – площа;
– площа; 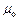 – магнітна стала;
– магнітна стала; 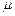 – магнітна проникність осердя.
– магнітна проникність осердя.
4. Енергія та об'ємна густина енергії магнітного поля
Енергія магнітного поля, зчепленого з контуром, локалізована в просторі і виражається формулою
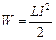 .
.
Об'ємна густина енергії магнітного поля соленоїда, яке однорідне і зосереджене всередині нього, виражається залежністю
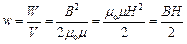 .
.
Тут враховано, що енергія магнітного поля соленоїда
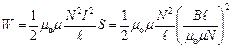 .
.
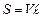 – об'єм соленоїда.
– об'єм соленоїда.
ЛЕКЦІЯ 13
Власні незгасаючі коливання
1. Коливання та їх типи
Коливання – це рух, або процеси, які характеризуються певною повторюваністю в часі.
Вільні коливання (власне коливання) – це коливання, що здійснюються за рахунок власної енергії при наступній відсутності зовнішніх впливів на коливальну систему. тобто систему. яка здійснює коливання.
За характером фізичних процесів розрізняють механічні, електромагнітні та інші типи коливань.
Гармонічні коливання. Гармонічні коливання величини 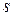 описуються рівнянням такого типу
описуються рівнянням такого типу
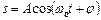 ,або
,або 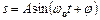 ,
,
де 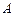 – амплітуда коливань;
– амплітуда коливань; 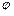 – початкова фаза в момент
– початкова фаза в момент 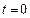 ;
; 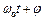 – фаза коливань в момент часу
– фаза коливань в момент часу 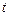 .
.
Фаза коливань визначає значення величини, що коливається, в даний момент часу.
Визначимо поняття періоду і частоти коливань.
Період гармонічного коливання – це проміжок часу Т, протягом якого фаза коливань отримує приріст 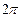 , тобто
, тобто
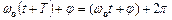 .
.
Звідси
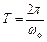 .
.
Частота коливань – це число повних коливань, які здійснюються за одиницю часу
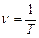 .
.
Одиниця коливань – 1Гц. 1Гц (герц) – це частота періодичного процесу, за якого за 1 с здійснюється один цикл процесу.
2. Механічні вільні гармонічні коливання, їх диференціальне рівняння
та розв'язок
Нехай матеріальна точка здійснює прямолінійні гармонічні коливання вздовж осі х біля положення рівноваги, яке приймемо за початок координат. Тоді залежність координати х від часу 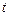 визначається рівнянням:
визначається рівнянням:
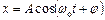 .
.
Визначимо швидкість 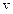 та прискорення
та прискорення 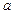 точки, що коливається.
точки, що коливається.
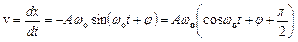 ;
;
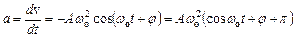 .
.
З наведених формул видно, що аммлітуда швидкості 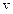 та прискорення
та прискорення 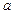 дорівнють
дорівнють 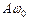 і
і 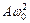 . При цьому фаза швидкості
. При цьому фаза швидкості 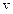 відрізняється від фази
відрізняється від фази 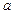 на
на 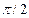 , а фаза прискорення
, а фаза прискорення 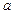 – на
– на 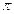 . В моменти часу, коли х = 0,
. В моменти часу, коли х = 0, 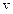 приймає своє найбільше значення; якщо х досягає свого найбільшого від'ємного значення, то
приймає своє найбільше значення; якщо х досягає свого найбільшого від'ємного значення, то 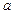 досягає найбільшого додатнього значення (див. рис. 13.1).
досягає найбільшого додатнього значення (див. рис. 13.1).
З виразу для 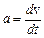 випливає таке диференціальне рівняння гармонічних коливань:
випливає таке диференціальне рівняння гармонічних коливань:
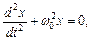
Розв'язок цього рівняння 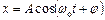 .
.
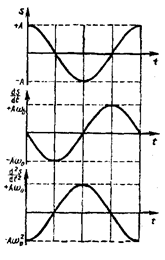
Рис. 13.1
Сила, що діє на матеріальну точку, що коливається,
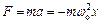
пропорційна зміщенню матеріальної точки і направлена в протилежну сторону (до положення рівноваги).
3. Енергія гармонічних коливань
Розглянемо енергію гармонічних коливань.
Кінетична енергія
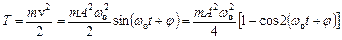 .
.
Потенціальна енергія
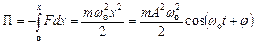
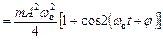 .
.
Повна енергія
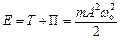 .
.
4. Електричний коливальний контур. Диференціальне рівняння власних електричних коливань та його розв'язок
Вільні коливання в коливальному контурі, що ідеалізується
Коливальний контур – це коло, що складається з ввімкнених послідовно котушки індуктивністю L, конденсатора ємністю С і резистора опором 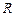 . Такий контур застосовується для збудження і підтримки електромагнітних коливань (періодичних процесів перетворення енергії електричного поля в енергію магнітного поля і навпаки). В ідеалізованому контурі опор
. Такий контур застосовується для збудження і підтримки електромагнітних коливань (періодичних процесів перетворення енергії електричного поля в енергію магнітного поля і навпаки). В ідеалізованому контурі опор 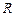 = 0.
= 0.
Послідовні стадії коливального процесу в ідеалізованомуконтурі і аналогія між електромагнітними і механічними коливаннями наведені на рис. 13.2.
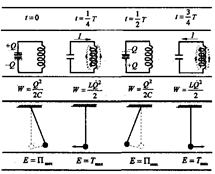
Рис. 13.2
Оскільки R 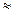 0, то згідно з законом збереження, повна енергія
0, то згідно з законом збереження, повна енергія
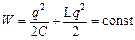 .
.
За відсутності втрат енергії в контурі здійснювались би періодичні незгасаючі коливання, тобто періодично змінювались (коливались) заряд 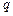 на обкладаннях конденсатора, напруга
на обкладаннях конденсатора, напруга 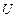 на конденсаторі і сила струму
на конденсаторі і сила струму 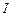 , що протікає через котушку індуктивності. Отже, в контурі виникають електричні коливання, причому коливання супроводжуються перетвореннями енергій електричного і магнітного полів.
, що протікає через котушку індуктивності. Отже, в контурі виникають електричні коливання, причому коливання супроводжуються перетвореннями енергій електричного і магнітного полів.
Диференціальне рівнянні електромагнітних коливань для ідеалізованого контура.
Для ідеалізованого контура (R 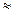 0) згідно з другим правилом Кирхгофа
0) згідно з другим правилом Кирхгофа
U С =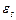
де U С =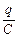 – напруга на конденсаторі;
– напруга на конденсаторі; 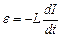 – е.р.с. самоіндукції, яка виникає в котушці у разі протікання в ній змінного струму. Підставивши ці вирази в U С =
– е.р.с. самоіндукції, яка виникає в котушці у разі протікання в ній змінного струму. Підставивши ці вирази в U С =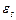 і врахувавши, що
і врахувавши, що 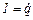 і
і 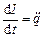 , отримаємо диференціальне рівняння коливань заряду в контурі:
, отримаємо диференціальне рівняння коливань заряду в контурі:
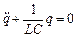
коливання вільні (в контурі відсутні зовнішні е. р. с.) гармонічні (R 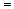 0)). Заряд
0)). Заряд 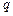 на обкладаннях конденсатора змінюється по гармонічному закону
на обкладаннях конденсатора змінюється по гармонічному закону
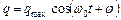 ,
,
де 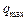 – амплітуда коливань заряду конденсатора з циклічною частотою
– амплітуда коливань заряду конденсатора з циклічною частотою 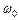 , яка називається власною частотою контура
, яка називається власною частотою контура
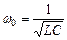
і періодом
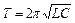
– формула Томсона.
Сила струму в коливальному контурі
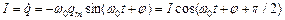 .
.
Напруга на конденсаторі
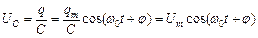 .
.
З двох останніх виразів випливає, що коливання струму І випереджають по фазі коливання заряду 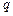 на
на 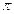 /2, тобто якщо струм досягає максимального значення, то заряд (і напруга) перетворюються в нуль, і навпаки.
/2, тобто якщо струм досягає максимального значення, то заряд (і напруга) перетворюються в нуль, і навпаки.
Згідно з законом збереження енергії
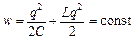 .
.
Додаток до лекції
Додавання гармонічних коливань
1. Метод векторних діаграм
Гармонічні коливання можна зобразити графічно, застосувавши метод векторних діаграм. Для цього з довільної точки О на осі х під кутом 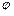 , який дорівнює початковій фазі коливання, відкладають вектор
, який дорівнює початковій фазі коливання, відкладають вектор 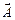 , модуль якого дорівнює амплітуді А даного коливання (рис. 13.1). Якщо цей вектор почати обертати з кутовою швидкістю
, модуль якого дорівнює амплітуді А даного коливання (рис. 13.1). Якщо цей вектор почати обертати з кутовою швидкістю 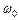 , яка дорівнює циклічній частоті коливань, то проекція кінця вектора переміщуватиметься по осі z і прийматиме значення від – А до + А, а величина, що коливається, змінюватиметься з часом за законом
, яка дорівнює циклічній частоті коливань, то проекція кінця вектора переміщуватиметься по осі z і прийматиме значення від – А до + А, а величина, що коливається, змінюватиметься з часом за законом
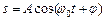 ,
,
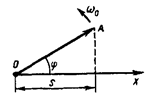
Рис. 13.1
У фізиці часто застосовують інший метод, який відрізняється від методу векторних амплітуд лише формою. В цьому методі величину, що коливається, представляють комплексним числом. Згідно з формулою Ейлера, для комплексних чисел
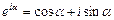 ,
,
де 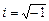 – уявна одиниця.
– уявна одиниця.
Тому рівняння гармонічного коливання 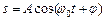 можна записати в комплексній формі:
можна записати в комплексній формі:
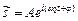 .
.
Дійсна частина цього виразу
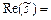
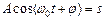
якраз і є гармонічним коливанням. Позначення Re дійсної частини опускають, тобто 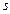 записують у вигляді:
записують у вигляді:
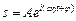
і вважають, що величина s, що коливається, дорівнює дійсній частині комплексного виразу, що стоїть в цьому рівнянні справа.
2. Додавання гармонічних коливань одного напрямку
В ряді випадків необхідно знати результуюче коливання, тобто підсумувати два гармонічні коливання одного напрямку і однакової частоти:
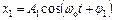 ;
;
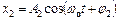 .
.
Рівняння результуючого коливання найпростіше знайти скориставшись векторних діаграм (рис 13.2):
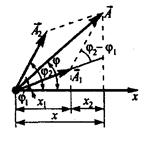
Рис. 13.2
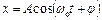 , (1)
, (1)
де амплітуда А і початкова фаза 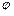 задаються співвідношеннями:
задаються співвідношеннями:
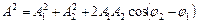 ;
;
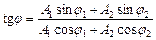 .
.
Результуюче коливання (1) – гармонічне і воно здійснюється в тому ж самому напрямку і з тією ж самою частотою, що й коливання, які підсумовуються.
Розглянемо два характерних випадки коливань:
1) 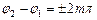 ,
, 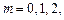 …. Тоді
…. Тоді 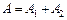 ;
;
2) 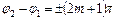 ,
, 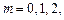 …. Тоді
…. Тоді 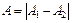 .
.
|
|
|
|
Дата добавления: 2014-01-03; Просмотров: 827; Нарушение авторских прав?; Мы поможем в написании вашей работы!