Маятники

Биття

Для практики важливим є випадок, коли додаються два гармонічних коливання з близькими частотами. Саме тоді виникає биття, тобто періодичне змінювання амплітуди коливань, яке виникає при підсумовуванні двох гармонічних коливання з близькими частотами.

Розглянемо додавання наступних коливань:

;

;

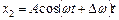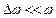, початкові фази обох коливань дорівнюють нулю

Результуюче коливання буде таким:

.

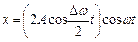Амплітуда биття: 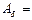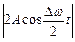; період биття: 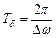(рис. 13.3).

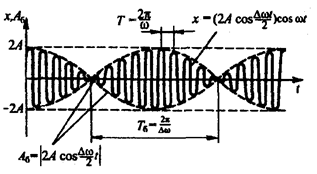
Рис. 13.3

4. Додавання взаємно перпендикулярних гармонічних коливань.

Поняття про фігури Ліссажу

Додаються гармонічні коливання однакової частоти 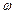, що відбуваються у взаємно перпендикулярних площинах

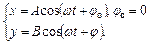
Рівняння траєкторії результуючого коливання можна отримати шляхом виключення параметра :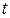

.

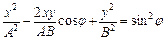Це рівняння еліпса, осі якого орієнтовані відносно координатних осей довільно.

Розглянемо два частинні випадки:

І. 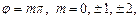…. Це випадок лінійно поляризованих коливань: еліпс вироджується у відрізок прямої лінії 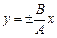, де знак плюс відповідає нулю і парним значенням (рис. 13.4, а), а мінус – непарним значенням (рис. 13.4, б),.

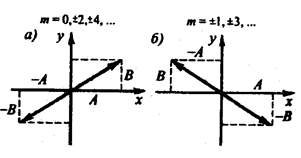
Рис. 13.4

ІІ. 1) 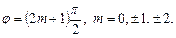…. 2) . Це випадок циркулярно поляризованих коливань: у разі виконання умови 1) матимемо еліпс, орієнтований відносно координатних осей; у разі виконання ще й умови 2) – еліпс вироджується в коло.

Фігури Ліссажу. Фігури Ліссажу – це замкнені траєкторії, які прочерчуються точкою, що здійснює одночасно два взаємно перпендикулярні коливання (рис. 13.5). Форма цих коливань залежить від співвідношення амплітуд, частот (на рисунку вказані зліва) і різниці фаз (на рисунку вказані зверху; різниця фаз приймається такою, що дорівнює ).

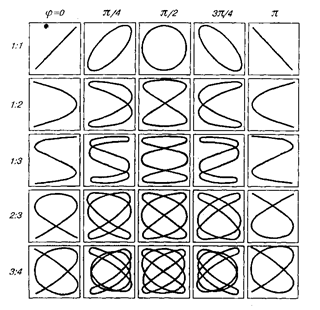
Рис. 13.5

ЛЕКЦІЯ 14

Згасаючі коливання

1. Згасаючі механічні коливання

Згасаючі коливання – це коливання, амплітуда яких внаслідок втрати енергії реальної коливальної системи з плином часу зменшується, перетворюючись в теплоту через тертя в механічних коливальних системах, омічні втрати та випромінювання електромагнітної енергії в електричних коливальних системах.

Закон згасаючих коливань визначається властивостями систем, що коливаються. Серед таких систем найпоширенішими є лінійні системи. Лінійні системи – це ідеалізовані реальні системи, в яких параметри, що визначають фізичні властивості системи, під час процесу коливань не змінюються (на відміну від нелінійних систем, в яких ці параметри змінюються нелінійно).

Різні за своєю природою лінійні системи описуються однаковими рівняннями, що дає можливість застосувати єдиний підхід до вивчення коливань різної фізичної природи.

Гармонічні коливання величини 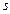описуються рівнянням такого типу

, ,

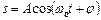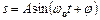де 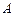– амплітуда коливань; 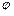– початкова фаза в момент 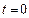; 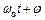– фаза коливань в момент часу .

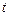Визначення періоду і частоти коливань:

; ; .

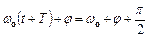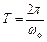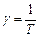Швидкість 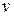та прискорення 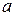точки

;

.

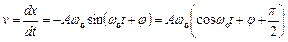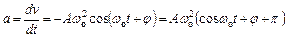Сила, що діє на матеріальну точку

.

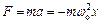Енергія гармонічних коливань

Кінетична енергія

.

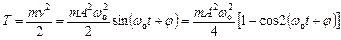Потенційна енергія

.

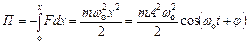Повна енергія

.

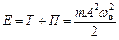Рівняння гармонічного осцилятора

.

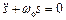Дата добавления: 2014-01-03