Математичний маятник

Пружний маятник

Рівняння руху маятника під дією сили :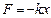

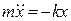
має розв'язок

; ; .

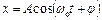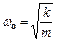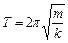Період малих коливань такого маятника

,

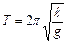де 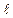– довжина маятника; 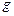– прискорення вільного падіння.

Фізичний маятник

Момент сили, що вертає, дорівнює

,

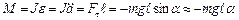де 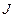– момент інерції відносно осі, що проходить через точку 0; 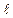– відстань між точкою підвісу і центром мас маятника; 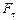– сила, що вертає; 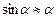відповідає малим коливанням маятника.

Рівняння фізичного маятника

; ,

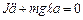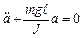де .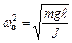

Фізичний маятник здійснює коливання з циклічною частотою 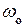і періодом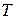

; ,

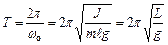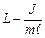де 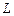– приведена довжина фізичного маятника.

2. Диференціальне рівняння вільних згасаючих коливань лінійної системи

та його розв'язок

Величина 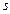, яка описує коливальний фізичний процес в лінійній системі, задовольняє диференціальному рівнянню:

,

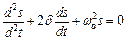де 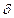– коефіцієнт згасання (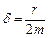– для механічних коливань і 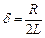– для електричних коливань); 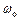– циклічна частота вільних коливань.

Розв'язок цього рівняння такий:

,

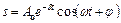де 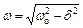– частота загасаючих коливань; 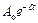– амплітуда згасаючих коливань.

Характеристики згасання такі: 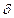– коефіцієнт згасання; 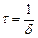– час релаксації – це час, протягом якого амплітуда згасаючих коливань зменшиться в е раз.

Період згасаючих коливань .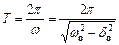

Вимушені коливання

Для пружного маятника, на який діє змушуюча сила :

,

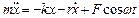або, враховуючи те, що , ,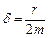

.

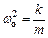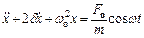Розв'язок цього рівняння:

,

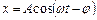де ; .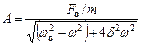

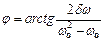Резонансна частота ()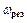

Ця частота визначається так:

,

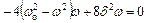звідки

.

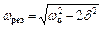Електричні коливання. Електричний коливальний контур

Згідно з законом Ома

,

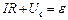де 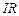– напруга на резисторі; 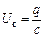– напруга на конденсаторі; 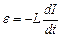– е. р. с. самоіндукції. Отже

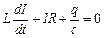
або

; ; ;

.

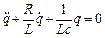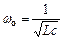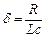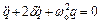Це рівняння має такий розв'язок:

,

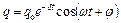де .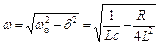

Згідно з законом збереження енергії

.

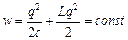ЛЕКЦІЯ 15

Вимушені коливання

1. Вимушені механічні коливання, диференціальне рівняння і його розв'язок. Характеристики вимушених коливань (частота, амплітуда, фаза)

Вимушені коливання – це незгасаючі коливання, що виникають під дією зовнішньої сили F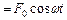, яка періодично змінюється (F₀ — амплітудне значення змушувальної сили).

Вимушені механічні коливання розглянемо на прикладі пружинного маятника.

Закон руху пружинного маятника. Для пружного маятника масою 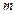, який здійснює малі коливання під дією пружної сили 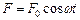, сила тертя пропорційна швидкості:

,

де 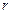– коефіцієнт опору; знак мінус вказує на протилежні напрями сили тертя і швидкості.

Отже, закон руху пружинного маятника з врахуванням змушувальної сили F 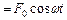, такий

.

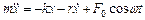З урахуванням того, що коефіцієнт згасання 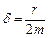, а 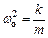, отримаємо диференційне рівняння:

.

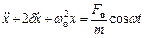Розв'язок цього рівняння:

,

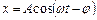де амплітуда 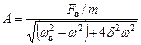(1); фаза .

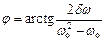2. Механічний резонанс

Розглянемо явище механічного резонансу. Це явище має місце за частоти, коли амплітуда зміщення досягне максимума. Така частота називається резонансно частотою (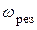). Ця частота визначається з такої умови:: треба продиференціювати підкорінний вираз у формулі (1) по 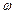і прирівняти його нулю:

,

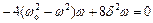звідки

.

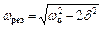Визначимо поняття механічний резонанс. Механічний резонанс – це явище різкого зростання амплітуди вимушених коливань при наближенні частоти змушувальної сили до частоти, яка дорівнює або наближається до власної частоти коливальної системи.

Резонансні криві – це криві залежності амплітуди А вимушених коливань від частоти 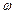при різних 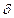. При 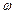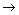0 всі криві досягають одного і того ж самого, відмінного від нуля, граничного значення 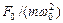, яке називається статичнимвідхиленням ( див. рис. 15.1).

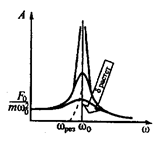
Рис. 15.1

3. Вимушені електромагнітні коливання, диференціальне рівняння

і його розв'язок і характеристики

Вимушені коливання – це незгасаючі коливання, що виникають під дією зовнішньої напруги 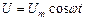, що періодично змінюється.

Закон Ома для контура з R, L, С. З урахуванням прикладеної напруги

,

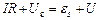де 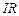– напруга на резисторі; 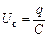– напруга на конденсаторі; 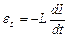– е.р.с. самоіндукції; .

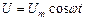Отже

.

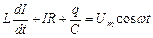Для виведення диференціального рівняння розділимо останнє рівняння на 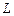і підставимо 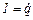, , 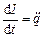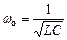; 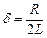. В результаті отримаємо

;

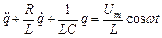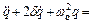
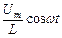
Це рівняння має такий розв'язок:

,

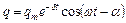де 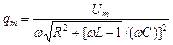; ; 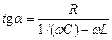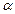– зсув по фазі між зарядом і прикладеною напругою.

Сила струму у разі сталих коливань дорівнюватиме:

,

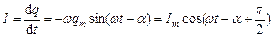де

.

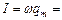
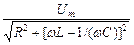Таким чином, сила струму має такий вид:

де 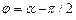– зсув по фазі між струмом і прикладеною напругою. Тоді можна показати, що

.

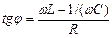4. Електричний резонанс і його використання в техніці

Розрізняють резонанс напруг і резонанс струмів. Розглянемо ці види резонансу докладніше.

Резонанс напруг (послідовний резонанс) може мати місце в колі змінного струму, що містить послідовно включені резистор, котушку індуктивності та конденсатор (див. рис. 15.2)

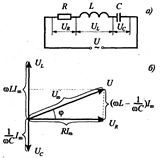
Рис. 15.2

Як видно з цього рисунка кут зсуву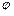визначає різницю фаз між струмом і напругою

.

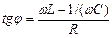З прямокутного трикутника випливає, що

,

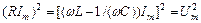звідки амплітудне значення сили струму

.

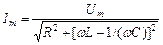Якщо напруга в електричному колі змінюється по закону 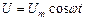, то струм в цьому колі буде такий:

.

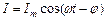Величина

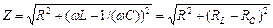
називається повним опором (імпедансом), а величина

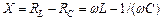(2)

реактивним опором.

Якщо в електричному колі з послідовно ввімкненими R, L, С

,

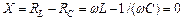то, згідно з формулою

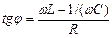
кут зсуву фаз між струмом і напругою стає таким, що дорівнює нулю: змінювання струму і напруги відбуваються синфазно. Умові (2) задовольняє резонансна частота:

.

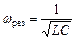В даному випадку повний опір Z = R і тому струм електричного кола визначається лише активним опором, приймаючи максимальні (можливі при даному 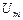) значення.

Резонанс напруг – це явище різкого зростання амплітуди сили струму в контурі при збігу циклічної частоти 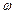зовнішньої змінної напруги з власною частотою 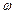₀ коливального контура.

Резонанс виразно проявляється лише при малому активному опорі контура (див. рис. 15.3).

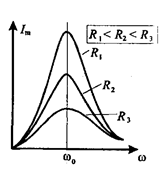
Рис. 15. 3

У випадку резонансу напруг 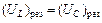, тобто однакові по амплітуді і протилежні по фазі (див. рис. 15.4).

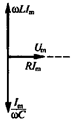
Рис. 15.4

Резонанс струмів (паралельний резонанс). Цей резонанс може відбутися в колі змінного струму, що містить паралельно ввімкнені конденсатор ємністю С і котушку індуктивністю L (див. рис. 15.5).Прикладена до кола напруга U = U_m cos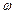 t. Активним опором обох гілок нехтуємо.

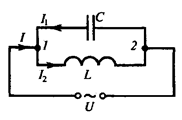
Рис. 15.5

Гілка 1 (в ній протікає струм І₁)

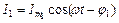
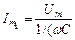
(враховано, що R = 0 і L = 0).

,

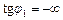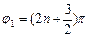, де n = 1, 2,....

Гілка 2 (в ній протікає струм І₂)

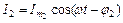
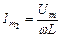
(враховано, що R = 0 і C = ).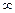

,

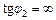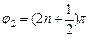, де n = 1, 2,....

Різниця фаз струмів в гілках: 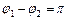, тобто струми в гілках протилежні по фазі. Амплітуда сили струму в зовнішньому (нерозгалуженому) колі

.

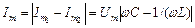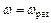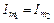Якщо , то і .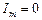

Резонанс струмів (паралельний резонанс) – це явище різкого зменшення амплітуди сили струму в зовнішньому ланцюзі, що живить паралельно включені конденсатор і катушку індуктивності, при наближенні частоти з прикладеної напруги до резонансної частоти з.

Амплітуда сили струму виявилася рівною нулю, тому що активним опором контура нехтуємо. Якщо врахувати опір R, то різниця фаз не буде дорівноювати 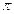, тому при резонансі струмів амплітуда сили струму буде відмінна від нуля, але прийме якнайменше можливе значення.

Автоколивання. Параметричний резонанс. Їх використання в техніці

В техніці в ряді випадків важливо підтримувати коливання незгасаючими. Для цього необхідно заповнювати втрати енергії реальної коливальної системи. Це досягається шляхом неперервного поповнення втрат в такій системі. Особливо важливими і широко застосовуваними в практиці є так звані автоколивання – незгасаючі коливання, які підтримуються в дисипативній системі за рахунок постійного діючого зовнішнього джерела енергії, причому властивості цих коливань визначаються самою системою.

Автоколивання принципово відрізняються від вільних незгасаючих коливань, що відбуваються без дії сил, а також від вимушених коливань, що відбуваються під дією періодичної сили. Автоколивальна система сама управляє зовнішніми діями, забезпечуючи узгодженість надходження енергії певними порціями в потрібний момент часу (в такт з її коливаннями).

Приклад автоколивальної системи – годинник, у якого храповий механізм підштовхує маятник в такт з його коливаннями. Енергія, що передається при цьому маятнику, поповнюється або за рахунок пружини, що розкручується, або за рахунок вантажу, що опускався. Коливання повітря в духових інструментах і органних трубах також виникають внаслідок автоколивань, підтримуваних повітряним струменем.

Автоколивальними системами є також двигуни внутрішнього згоряння, парові турбіни, ламповий генератор та ін.

Дата добавления: 2014-01-03