Детерминированные системы с последействием

Детерминированные системы без последствия с вх. сигналами двух классов.

Операторы переходов и выходов.

Рассм. 4 и 5 предположения.

В рамках 4:

[Все будет справедливо для систем без последействия]

Нас будет интересовать сост-е системы в люб мом вр. Z(t), определяемое:

z(t)=H{t, t_o, z(t_o), (t, x_L]_to^t} (1)

Здесь Н – это оператор перехода, аргументы которого:

tÎT - время

t_oÎT – текущий момент

z(t_o) ÎZ

{(t, x_L]_to^t} – мн-во входных отрывков для мом вр. t.

В рамках соотн-я (1) получение люб. нового зн-я отн. сост-я системы можно рассм. как отобр-е мн-в T в Z.

Наряду с непрерыв. сообщ. рассм. и конечные сообщения:

z(t)=H{t; t_o; z(t_o); (t₁, x₁); (t₂, x₂);…(t_k, x_k)} (2)

Наряду с необ-тью опр-я сост-я системы, возникает необ-ть нах-я построения в люб мом вр.

y(t)=G{t_o, t, z(t_o), (t, x_L]_to^t} (3)

G – оператор выходов системы. Здесь все эл-ты (аргументы) явл эл-тами соотв. мн-в.

На практике вместо (3) исп. другая запись:

y(t)=G{t, z(t)} (4)

И теперь, если учесть запись (2), то (4):

y(t)=G{t, H{t, t_o, z(t_o), {t,x_L]_to^t} (5)

Введем понятие:

H*=HxG (6) – оператор ф-я системы

Все сказанное отн. к детерминированным системам без последействия.

Развитие теории и практики систем настоятельно выдвигает проблемы, изучение кот. выходит за рамки детерминированных систем без последействия.

Расширение понятия систем в связи с этим идет по 3 направлениям:

1) связано с учетом специфики воздействий, кот. можно рассм. в различных классах;

2) связано с учетом последействия;

3) связано с учетом случайного хар-ра воздействий.

Рассм. в рамках 1-го напр-я.

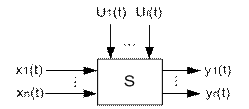
По аналогии с вопр-ми рассм-я вх и вых сигналов перейдем к понятию прям. произв-я управл-х сигналов.

uÎU

uiÎUi;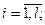

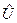=U₁xU₂x…U _l (1) – пространство управляющих сигналов.

Рассм. отображение T→U; u=M(t) (2)

(t, u) – управляющее воздействие

(t, u_m]_t1^t2 (3) - отрывок управл-го воздействия.

На практике, несмотря на то, что важно разделение вх сигналов на X и на U, очень часто пользуются понятием обобщенный вх. сигнал:

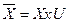(4)

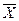=(x₁, x₂,…x_n; u₁…u _l);

Моменты поступления сигналов X и U могут не совпадать:

Говоря о паре: (x; u)Þ(x_Ø,u) Þ(x,u_Ø)

В д.сл. обобщ. вх. сообщения опред-ся 3-мя пар-рами: (t, x, u).

И в этом сл. мы тоже может говорить об отрывке вх. сигнала: (t, x, u_m]_t1^t2 .

Теперь мы можем говорить о получении и формировании состояния системы без последействия:

z(t)=H{t, to, z(t_o), (t, x_L, u_m]_t1^t2} (5)

Наряду с обобщ. вх. сообщ. и (5) на практике исп. и другое, с учетом специфики 2-х классов:

z(t)=H{t, t_o, z(t_o), (t, x_L]_t1^t2, (t, u_m]_t1^t2} (6)

Пример: модель этой системы:

- это лин. система авт. упр-я:

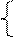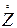(*) =AZ+BU+Df;

Y=CZ; z(t_o)=z_o

1)

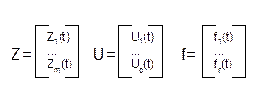
A, B, C и D – матрицы соотв. размерностей.

Y – это выходные сигналы yi, где i=.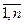

Эту системы мы можем интерпретировать как детерминир-ую систему с вх. сигналами (сообщ-ми) 2-х классов.

К экзамену еще примеры

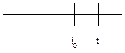
t>t_o

Поведение в t будет опред-ся не только состоянием t_o, но и <t_o.

Нам нужно при построении моделей учесть это последействие.

Введем мн-во В₀ÌТ, для кот. хар-но, что t<t_o.

Введём отображение: z=w(t)

И теперь с учетом сказанного, можем записать поведение системы z(t) в любой. мом. вр. t, где t>t_o:

z(t)=H{t, t_o, z(t_o), (t_Bo, z_w), (t, x_L]_to^t} (1)

учитываем последействие.

Здесь исп. вся введенная терминология.

tÎT, toÎT; ВоÌТ; (t_Bo, z_w)={(t_Bo; z_w)}; (t, x_L]_to^tÎ{(t, x_L]_to^t}

Дата добавления: 2014-01-03