Примеры применения МСП к исследованию систем

При решении задач любых сложных систем очень широко исп аппарат МСП. Это объясняется: 1) его простотой (это или сист обыкн лин диф ур-й или обыч лин ур-й); 2) при исследовании сложных систем наряду с необходимостью определения обобщённых целевых ф-й возникает необх-ть определения достаточно большого кол-ва частных показателей, таких как определение среднего времени передачи И-и, ср времени формирования управляющего воздействия, ср времени первичной обработки сигналов и многое другое.

Многие усреднённые хар-ки опред-ся для объед-я подсистем в системы. В планировании гибких производств без этого аппарата никуда.

Послед-ть действий при исследовании систем по схеме МСП:

1. выделение всех физ состояний системы (неоднозначно и определяется особенностями решаемой задачи)

2. составление графа состояний системы

3. получение размеченного графа (интенсивности сразу не даны как правило Þ трудно)

4. составление ур-й Колмогорова

5. задание нач условий

6. Решение.

Пример 1: локальная система обработки детали на станке. Она нах на складе. Её нужно доставить к раб месту, обработать и возвратить инструмент в отдел укомплектования.

4 сост-я:

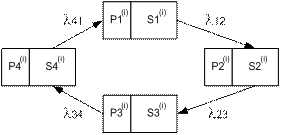
(i) – т.е. эта система справедлива для любого инструмента или любой детали. Если этот процесс протяжённый, то можем воспользоваться предельными вероятностями.

Пример 2: МСП исп также во всём, что связано с наведением на цель: организация головки самонаведения. Сост-я:

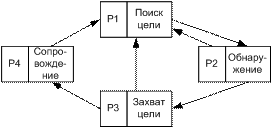
Здесь Pi – ф-и времени.

Эти задачи решаются на этапе отладки головки самонаведения на спец макетах.

Пример 3: Исследование микропроцессорных систем. Требуется исследовать влияние параметров программ на хар-ки обмена в микропроцессорных системах с общей магистралью. Рассмотрим простейший случай: 2-х процессорную систему:

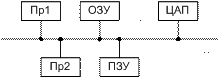
Каждый процеесор может нах в фазе автономной работы. Сост-я: S0 – фаза автономной работы; S1 – обмен; S2 – ожидание. Для каждого из процеесоров фаза автономной работы имеет показательный закон с интенсивностями li: 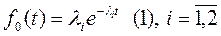. Фаза обмена также имеет показательный закон с интенсивностями mi: .

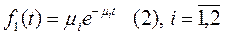В конечном итоге нас интересуют вопросы исследования зависимости коэффициента загрузки магистрали h-? и коэф-ты удлинения программ ei-? для данной структуры в зав от временных хар-к программ.

1) выделяем состояния: S1(0,0); S2(1,0); S3(0,1); S4(1,2); S5(2,1)

2), 3) строим граф:

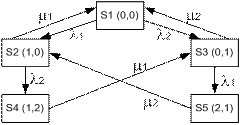
4) определим h и ei. Для этого определим пред вероятности P(0,0) …

Тогда h=1-P(0,0)

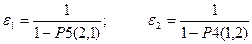
Дата добавления: 2014-01-03