Краткие теоретические и учебно-методические материалы по теме практической работы

Практическая работа

Пример 1: Вычислить.

Пример 2: Вычислить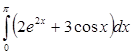

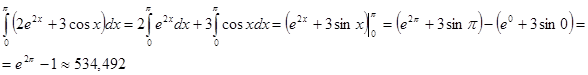
Пример 3: Вычислить :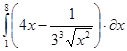

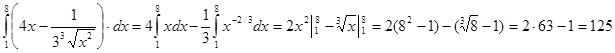
Пример 4: Вычислить: :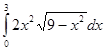

.

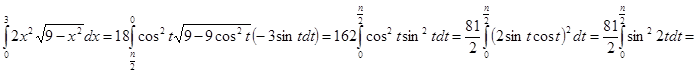
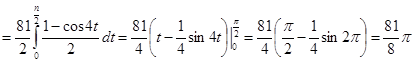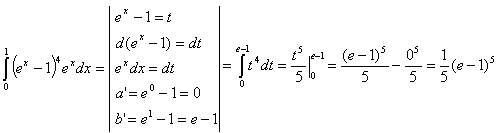
«Вычисление неопределенных интегралов»

Учебная цель: научиться вычислять неопределенный интеграл методом непосредственного интегрирования и способом подстановки.

1. Неопределенный интеграл

Определение:Совокупность всех первообразных функций F (x) + c для функции f (x) на некотором промежутке называется неопределённым интегралом и обозначается:

∫ f (x) dx

Таким образом,

∫ f (x) dx = F(x) + c,

где f(x) dx называется подынтегральным выражением, а c -произвольной постоянной интегрирования.

Например: ∫ 2xdx = x² + c, так как (x² + c)’= 2x.

Процесс нахождения первообразной функции называется интегрированием.

2. Метод непосредственного интегрирования.

Под непосредственным интегрированием понимают способ интегрирования, при котором данный интеграл путем тождественных преобразований подынтегральной функции и применения свойств неопределенного интеграла приводятся к одному или нескольким табличным интегралам.

Свойства неопределённого интеграла

1) d ∫ f(x) dx= f(x) dx

2) ∫ dF (x) =F(x) + c

3) ∫ a ∙ f(x) dx=a ∫ f(x) dx

4) ∫[f₁ (x) + f₂ (x) – f₃ (x)] dx = ∫ f₁ (x) dx + ∫ f₂ (x) dx - ∫ f₃ (x) dx

Формулы интегрирования

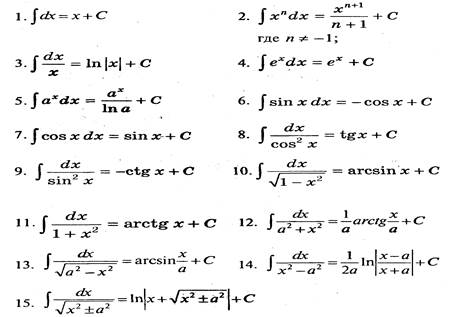
3. Интегрирование методом замены переменной интегрирования

Замена переменной производится с помощью подстановки:

t = ψ (x), где t – новая переменная. В этом случае формула замены переменной

∫ f [ψ(x)]ψ’(x) dx = ∫ f(t) dt.

В полученном после интегрирования в правой части выражения надо перейти снова к аргументу x:

Дата добавления: 2017-01-14