
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Заявка принимается до 11 января 2017 года
|
|
|
|
Завдання № 10.
Приклади.
Частина 2.
Завдання № 5.
Завдання № 4.
Завдання № 3.
Приклад 2.
Приклад 1.
Приклад 2.
Приклад 1.
Приклади.
Частина 1
Завдання № 1. Розв’язати систему лінійних алгебраїчних рівнянь:
а) методом Крамера;
б) методом матричного числення;
в) методом Гауса.
Дана система трьох лінійних алгебраїчних рівнянь с трьома невідомими: 
Потрібно:
а) знайти рішення системи за допомогою формул Крамера;
б) розв’язати систему за допомогою оберненої матриці.
а)при розв’язанні систем n лінійних рівнянь з n невідомими
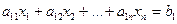 ;
;
 ;
;
…

можна застосовувати формули Крамера 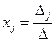
 , де
, де  - визначник системи з коефіцієнтів при невідомих
- визначник системи з коефіцієнтів при невідомих  , а
, а  - визначник, який отримується з
- визначник, який отримується з  заміною елементів j –го стовпця елементами стовпця вільних членів
заміною елементів j –го стовпця елементами стовпця вільних членів  стосовно.
стосовно.
Розв’яжемо систему за допомогою формул Крамера. Для цього складемо головний визначник системи з коефіцієнтів при невідомих у лівих частинах рівнянь та три допоміжних визначника:

Обчислимо ці визначники:

Так як ∆ ≠ 0, то дана система має єдине рішення.
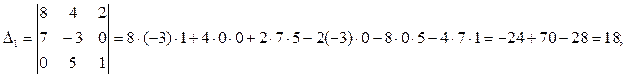

 Знайдемо рішення системи по формулам Крамера:
Знайдемо рішення системи по формулам Крамера:

б) Запишемо систему у матричному вигляді:
 , або AX = B, де
, або AX = B, де 
(у другому рівнянні системи відсутня невідома х 3, тому а 23 = 0).
Розв’яжемо систему за допомогою оберненої матриці.
1. Визначник  тоді обернена матриця існує.
тоді обернена матриця існує.
2. Щоб знайти союзну матрицю А * до матриці А, необхідно обчислити алгебраїчні доповнення всіх її елементів:
 Тоді союзна матриця:
Тоді союзна матриця: 
3. Знайдемо обернену матрицю:
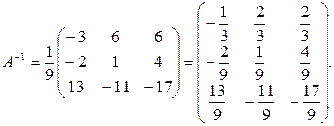
4. Отримаємо рішення системи за допомогою оберненої матриці (правило «строка на стовпець»):

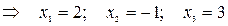 .
.
Рішення, яке отримано матричним способом, співпадає с тим, яке отримано по формулам Крамера, що підтверджує правильність цього рішення.
Відповідь:
а) рішення системи по формулам Крамера:  ;
;
б) рішення системи за допомогою оберненої матриці:  .
.
Розв'язати систему лінійних алгебраїчних рівнянь методом Гауса (послідовного видалення невідомих).
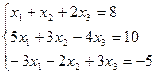
а) випишемо розширену матрицю цієї системи.
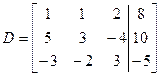
б) зведемо матрицю D до «трикутного» виду, з котрого зможемо знайти рішення системи.
Для цього зробимо над строками матриці D елементарні перетворення. До ним відносяться:
- зміна порядку строк (відповідно зміні порядку рівнянь);
- множення строки на відмінне від нуля число (відповідно множенню відповідних рівнянь на це число);
- додання до будь-якої строки матриці D будь-якої іншої її строки, яка помножена на число (відповідає доданню до одного з рівнянь системи другого рівняння, помноженого на число).
Таким чином, у процесі приведення матриці системи до «трикутного» виду виконаємо наступні перетворення:
1) віднімемо з другої строки першу строку, помножену на 5;
2) до третьої строки додамо першу строку, помножену на 3;
3) першу строку залишимо без зміни.
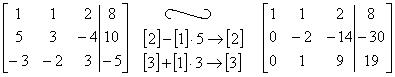

Помножимо другу строку на  .
.
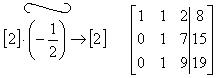
Віднімемо з третьої строки другу і тим самим приведемо розширену матрицю до «трикутного» виду.
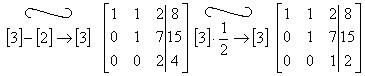
Це розширена матриця системи,

яка еквівалентна початковій системі.
Підставляємо значення  у друге рівняння, знаходимо
у друге рівняння, знаходимо  :
:
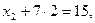

Підставляємо значення  и
и  у перше рівняння, знаходимо
у перше рівняння, знаходимо  :
:


Відповідь:  ,
,  ,
,  .
.
Завдання № 2. За допомогою теореми Кронекера-Капелі дослідити на сумісність систему рівнянь. У випадку додатної відповіді знайти загальне та яке-небудь часткове рішення системи.

Розв’язання.


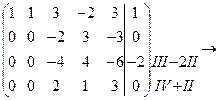
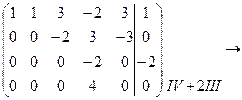

Відповідь: система несумісна.

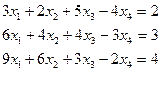
Розв’язання.




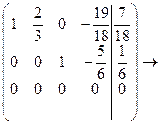
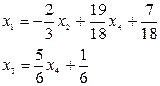
Відповідь: загальний розв’язок системи:  ;
;
частковий розв’язок системи:  .
.
Приклад. Дано координати трьох векторів: 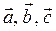 і вектор
і вектор  :
:
 ,
, 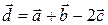 .
.
Потрібно:
1) обчислити модуль вектора  ;
;
2) знайти координати вектора  ;
;
3) знайти кут φ між векторами  и
и  ;
;
4) обчислити проекцію вектора  на напрямок вектора
на напрямок вектора  ;
;
5) обчислити площу трикутника, побудованого на векторах  і
і  ;
;
6) обчислити об'єм паралелепіпеду, побудованого на векторах 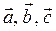 .
.
Розв’язання.
1) Знайдемо модуль вектора  :
:

 .
.
2) Знайдемо координати вектора 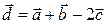 :
:

тоді 
3) Знайдемо косинус кута між векторами  и
и  :
:
 .
.
Для цього обчислимо скалярний добуток  и
и  за формулою:
за формулою: 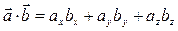 = –2∙0 + 2∙(–3) + (–1)∙4 = –10, потім модуль вектора
= –2∙0 + 2∙(–3) + (–1)∙4 = –10, потім модуль вектора  :
:  , тоді і
, тоді і 
4) Проекцію вектора  на напрямок вектора
на напрямок вектора  обчислимо за формулою:
обчислимо за формулою:

5) Знайдемо площу трикутника, побудованого на векторах  і
і  . Для цього спочатку знаходимо векторний добуток цих векторів:
. Для цього спочатку знаходимо векторний добуток цих векторів:
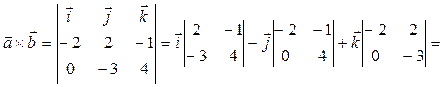

Отже, площа трикутника, побудованого на векторах  і
і  :
:
 (кв.од.).
(кв.од.).
6) Для обчислення об'єму паралелепіпеду, побудованого на векторах 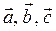 знаходимо мішаний добуток цих векторів:
знаходимо мішаний добуток цих векторів:

тоді об'єм паралелепіпеду: 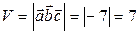 .
.
Відповіді:
1) модуль вектора  :
: 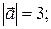
2) координати вектора  :
: 
3) кут між векторами  и
и  :
: 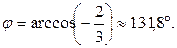
4) проекція вектора  на напрямок вектора
на напрямок вектора  :
: 
5) площа трикутника, побудованого на векторах  і
і  :
:  (кв.од.);
(кв.од.);
6) об'єм паралелепіпеду, побудованого на векторах:  (куб.од.).
(куб.од.).
Приклад. Дано координати точок – вершин піраміди ABCD:
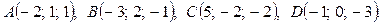 .
.
Треба:
1) обчислити довжину ребра AB;
2) знайти рівняння площини грані ABC;
3) найти кут  між гранями ABC та BCD;
між гранями ABC та BCD;
4) скласти параметричні рівняння прямої AB;
5) скласти канонічне рівняння висоти піраміди DK, яка проведена з вершини D;
6) знайти координати точки перетину прямої DK та грані ABC;
7) знайти кут  між ребрами AB та BC;
між ребрами AB та BC;
8) знайти кут  між ребром AD та гранню ABC;
між ребром AD та гранню ABC;
9) зробити креслення піраміди в системі координат.
Розв’язання.
1) Знайдемо довжину ребра  :
:

2) Щоб получити рівняння площини грані ABC, необхідно знайти вектор, який перпендикулярний площині ABC, тобто вектор, що перпендикулярний векторам  и
и  . Одним з таких векторів є векторний добуток
. Одним з таких векторів є векторний добуток  на
на  . Для того, щоб знайти його, спочатку обчислимо координати векторів:
. Для того, щоб знайти його, спочатку обчислимо координати векторів:
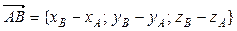 ={–3–(–2); 2–1; –1–1} = {–1; 1; –2},
={–3–(–2); 2–1; –1–1} = {–1; 1; –2},
 ={7; –3; –3}.
={7; –3; –3}.
Знайдемо векторний добуток векторів  та
та  :
:
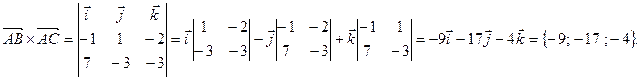 У якості вектора нормалі до площини ABC можливо взяти любий вектор, який колінеарний отриманому, наприклад,
У якості вектора нормалі до площини ABC можливо взяти любий вектор, який колінеарний отриманому, наприклад,  = (9; 17; 4). Використовуємо рівняння площини, яка проходить через точку
= (9; 17; 4). Використовуємо рівняння площини, яка проходить через точку  перпендикулярно вектору
перпендикулярно вектору  :
: 
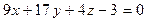 – рівняння площини грані ABC.
– рівняння площини грані ABC.
3) Перед, тим як знайти кут  між гранями ABC та BCD, отримаємо рівняння грані BCD. Для цього застосовуємо рівняння площини, яка проходить через три задані точки
між гранями ABC та BCD, отримаємо рівняння грані BCD. Для цього застосовуємо рівняння площини, яка проходить через три задані точки 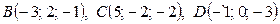 :
:

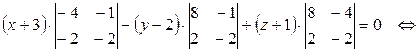

 – рівняння грані BCD.
– рівняння грані BCD.
З рівняння площини BCD візьмемо координати вектора нормалі  , перпендикулярного до цієї площини:
, перпендикулярного до цієї площини:  ={3; 7; –4}.
={3; 7; –4}.
Знайдемо косинус кута  між площинами (гранями) ABC та BCD:
між площинами (гранями) ABC та BCD:

Звідси 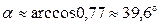 .
.
4) Рівняння ребра AB можна записати як параметричні рівняння прямої, яка проходить через точку A (–2;1;1) та має напрямний вектор  = (–1; 1; –2):
= (–1; 1; –2):
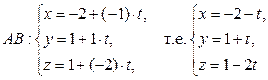 – параметричні рівняння прямої AB.
– параметричні рівняння прямої AB.
Другий спосіб: можна використати рівняння прямої, яка проходить через дві точки  :
:

звідки, якщо позначити кожну з дробів буквою t, отримаємо:

 – параметричні рівняння AB.
– параметричні рівняння AB.
5) Висота піраміди DK – це пряма, яка проведена з вершини D перпендикулярно грані ABC. Вона має напрямний вектор  , колінеарний вектору нормалі площини ABC. Можна взяти, наприклад,
, колінеарний вектору нормалі площини ABC. Можна взяти, наприклад,  =
=  = {9; 17; 4}. Запишемо канонічне рівняння висоти DK з використанням точки D (–1; 0; –3) та вектора
= {9; 17; 4}. Запишемо канонічне рівняння висоти DK з використанням точки D (–1; 0; –3) та вектора  =(9; 17; 4):
=(9; 17; 4):
 – канонічне рівняння прямої DK.
– канонічне рівняння прямої DK.
6) Перед тим, як знайти точку перетину прямої DK та грані ABC, отримаємо параметричні рівняння прямої DK. Позначимо кожну з дробів у канонічному рівнянні буквою t, отримаємо:

 – параметричні рівняння прямої DK.
– параметричні рівняння прямої DK.
Точка перетину DK та грані ABC (точка К) лежить на прямій, а значить, має координати 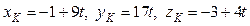 , та належить площині, тобто її координати задовольняють рівнянню площини ABC. Тому координати точки K знайдемо, розв’язуючи систему:
, та належить площині, тобто її координати задовольняють рівнянню площини ABC. Тому координати точки K знайдемо, розв’язуючи систему:

Розв’яжемо останнє рівняння відносно t:
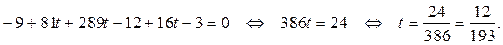
Обчислимо координати точки K, для чого підставимо знайдене значенняпараметра t у перші три рівняння системи:
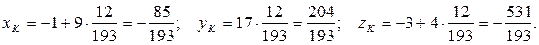

Так, точка перетину прямої DK і грані ABC:  .
.
7) Кут  між ребрами AB і BC знайдемо, як кут між напрямними векторами прямих AB и BC:
між ребрами AB і BC знайдемо, як кут між напрямними векторами прямих AB и BC:  = (–1; 1; –2) та
= (–1; 1; –2) та 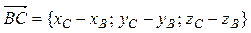 =(8; –4; –1). Обчислимо косинус кута
=(8; –4; –1). Обчислимо косинус кута  :
:
 Тоді кут між ребрами AB і BC:
Тоді кут між ребрами AB і BC: 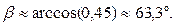
8) Щоб визначити кут  між ребром AD та гранню ABC,
між ребром AD та гранню ABC,
знайдемо напрямний вектор прямої:  =(1; –1; –4). Площина ABC має вектор нормалі
=(1; –1; –4). Площина ABC має вектор нормалі  = (9; 17; 4). Синус кута
= (9; 17; 4). Синус кута  між прямою
між прямою  та площиною ABC можна обчислити:
та площиною ABC можна обчислити:
 Тоді кут між ребром AD та гранню ABC:
Тоді кут між ребром AD та гранню ABC: 
9) Виконаємо креслення піраміди у системі координат (рис.).

Відповіді:
1) 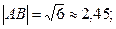
2) АВС: 
3)  ;
;
4) 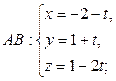
5) DK:  ; 6)
; 6)  ;
;
7)  ; 8)
; 8)  ;
;
9) креслення піраміди на рис.
Приклад. Дано координати вершин трикутника АВС: А (–3; –1), В (4; 6), С (8; –2).
Потрібно:
1) Обчислити довжину сторони ВС;
2) скласти рівняння сторони ВС;
3) знайти внутрішній кут трикутника при вершині В;
4) скласти рівняння висоти АК, яка проведена з вершини А;
5) знайти координати центра тяжіння однорідного трикутника (точки перетину його медіан);
6) зробити креслення у системі координат.
Розв’язання.
1) Обчислимо довжину сторони ВС за формулою:
| BС |=  =
= 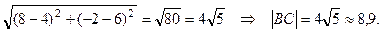
2) Складемо рівняння сторони ВС, застосовуючи формулу:


 y = –2 x + 14 – рівняння ВС.
y = –2 x + 14 – рівняння ВС.
3) Внутрішній кут трикутника при вершині В знайдемо як кут між прямими ВА і ВС. Для цього спочатку обчислимо кутовий коефіцієнт прямої ВА за формулою:
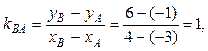
та візьмемо з рівняння прямої ВС кутовий коефіцієнт прямої ВС:  .
.
З розташування точок A, B, C на координатній площині видно, що кут В у трикутнику ABC – гострий, тому обчислимо

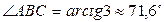 .
.
4) Для отримання рівняння висоти АK, проведеної з вершини А, застосовуємо рівняння пучка прямих та умову перпендикулярності прямих. Спочатку обчислимо кутовий коефіцієнт прямої АK. Так як 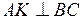 , то
, то 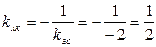 .
.
Рівняння прямої AK отримаємо за формулою:
у – уА = kAK (x – x A)  у – (–1) =
у – (–1) =  (x – (–3))
(x – (–3)) 
x –2 y + 1 = 0 – рівняння AK.
5) Для визначення координат центра тяжіння трикутника застосовуємо властивість точки перетину його медіан: якщо AМ – медіана трикутника і P – точка перетину його медіан, то P розподіляє AМ у відношенні 2: 1, починаючи від точки А, тобто 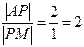 .
.
Основа медіани AМ – точка М є серединою відрізка ВС. Знайдемо координати точки М за формулами:
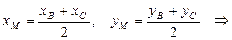
 М (6; 2).
М (6; 2).
Тепер, коли координати кінців відрізка AМ відомі, знайдемо координати точки P, яка розподіляє AМ у відношенні  = 2, починаючи від точки А, за формулами ділення відрізка у заданому відношенні:
= 2, починаючи від точки А, за формулами ділення відрізка у заданому відношенні:
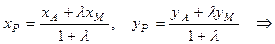


P (3; 1) – центр тяжіння трикутника АВС.
6) Побудуємо креслення до прикладу у системі координат ХОY (рис.). Отримані при рішенні задачі результати не суперечать кресленню.

Відповіді:
1) довжина сторони | BС | = 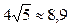 ;
;
2) рівняння сторони ВС: y = –2 x + 14;
3) кут при вершині В:  ;
;
4) рівняння висоти АK: x –2 y + 1 = 0;
5) координати центра тяжінн трикутника P (3; 1);
6) креслення на рис.
Завдання № 6. Обчислити границі функцій без використання правила Лопіталя:
а) 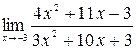 ; б)
; б) 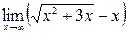 ;
;
в) 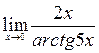 ; г)
; г)  .
.
Розв’язання.
а) підстановка граничного значення аргументу 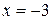 приводе до невизначеності виду
приводе до невизначеності виду 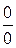 .
.
Для усунення цієї невизначеності розкладемо чисельник та знаменник дробу на множники та скоротимо дріб на множник 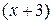 . Таке скорочення можливо, так як множник
. Таке скорочення можливо, так як множник  відмінний від нуля при
відмінний від нуля при  :
:
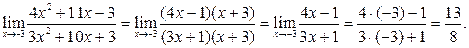
б) при  вираз
вираз 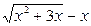 дає невизначеність виду
дає невизначеність виду 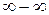 . Для її усунення помножимо та поділимо цей вираз на
. Для її усунення помножимо та поділимо цей вираз на  :
:

в) позначимо 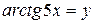 . Тоді
. Тоді  та
та 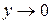 при
при 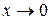 . Застосовуємо властивості границь та формулу першої визначної границі
. Застосовуємо властивості границь та формулу першої визначної границі 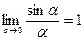 , маємо:
, маємо:

г) при  вираз
вираз  є невизначеністю виду
є невизначеністю виду  . Для усунення цієї невизначеності зобразимо основу степені у вигляді суми 1 та нескінченно малої при
. Для усунення цієї невизначеності зобразимо основу степені у вигляді суми 1 та нескінченно малої при  величини і застосуємо формулу другої визначної границі:
величини і застосуємо формулу другої визначної границі:
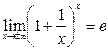 .
.
Тоді маємо:
 .
.
Нехай  . Тоді
. Тоді 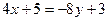 і
і  при
при  . Перейдемо до змінної у, отримаємо:
. Перейдемо до змінної у, отримаємо:
 .
.
Завдання № 7. Обчислити границі функцій з використанням правила Лопіталя.
Знайти:  .
.
Розв’язання.
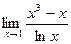
 =[Застосовуємо правило Лопіталя:
=[Застосовуємо правило Лопіталя:  ]=
]=  .
.
Завдання № 8. Знайти похідні  даних функцій.
даних функцій.
а) 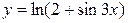 ; б)
; б)  ; в)
; в)  ;
;
г) 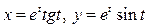 .
.
Розв’язання.
а) послідовно застосовуючи правило диференціювання складної функції, правила та формули диференціювання, маємо:
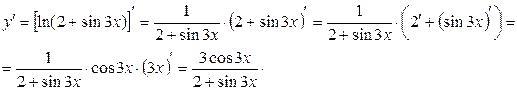
б)

в) у даному випадку функціональна залежність задана у неявному вигляді. Для знаходження похідної  треба продиференціювати по змінній х обидві части рівняння, вважаючи при цьому у функцією від х, а потім отримане рівняння вирішити відносно
треба продиференціювати по змінній х обидві части рівняння, вважаючи при цьому у функцією від х, а потім отримане рівняння вирішити відносно  :
:

З останнього рівняння знаходимо  :
:

г) 

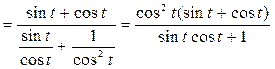 .
.
Завдання № 9. Провести повне дослідження функції та побудувати її графік.
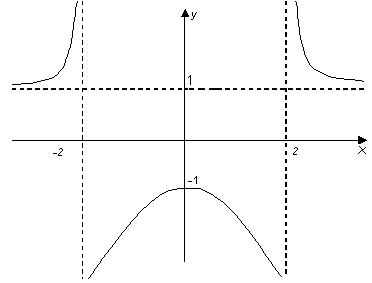
Приклад 1. Побудувати графік функції
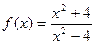
Розв’язання.
1) Область визначення функції f:
Х= 



 .
.
2) Функція парна. Тому її графік симетричний відносно осі ординат.
3) Функція не є періодичною. Це випливає навіть з того, що вона невизначена лише у двох точках.
4) Графік функції перетинає вісь ординат у точці (0;1). Нулі функції відсутні. Отже, графік функції не перетинає вісь абсцис.
5) Дослідимо функцію на монотонність та критичні точки. Для цього знайдемо похідну

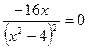 ;
;
х =0–критична точка.
Для 



 . Отже, на цих проміжках функція зростає. Оскільки функція парна, то на проміжках
. Отже, на цих проміжках функція зростає. Оскільки функція парна, то на проміжках 

 вона спадає. Тоді точка х =0 є точкою локального максимуму. Знайдемо його значення:
вона спадає. Тоді точка х =0 є точкою локального максимуму. Знайдемо його значення:
 .
.
6) Дослідимо функцію на опуклість та точки перегину:
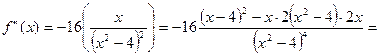
 .
.
На проміжках 


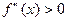 . Отже, графік функції опуклий вниз. На проміжку
. Отже, графік функції опуклий вниз. На проміжку 
 , а тому графік функції опуклий вгору.
, а тому графік функції опуклий вгору.
Точки перегину відсутні.
7) Оскільки  , то пряма у=1 є горизонтальною асимптотою для графіка функції.
, то пряма у=1 є горизонтальною асимптотою для графіка функції.
Дослідимо поведінку функції біля точок х =2, х =-2:
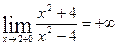 ,
, 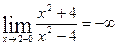 .
.
Отже, в точці х =2 функція має розрив другого роду, а пряма х =2 є вертикальною асимптотою. Враховуючи парність функції, робимо висновки, що пряма х =-2 також є вертикальною асимптотою.
 .
.
Приклад 1. Знайти частинні похідні функції  .
.
Розв’язання.
Знайдемо  при умові, що
при умові, що  , а, як слід, і її похідна
, а, як слід, і її похідна  .
.
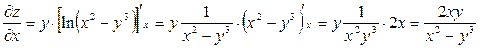 .
.
(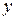 як
як  винесли за знак похідної).
винесли за знак похідної).
Знайдемо  , враховуючи, що
, враховуючи, що 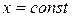 , а, як слід, і похідна
, а, як слід, і похідна  , тоді
, тоді

 .
.
Приклад 1. Дана функція  . Знайти всі її частинні похідні 2-го порядку і переконатися, що
. Знайти всі її частинні похідні 2-го порядку і переконатися, що  .
.
Розв’язання.
 ;
;  ;
;

 ;
;

 ;
;

 ;
;

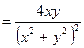 .
.
З останніх рівностей бачимо, що  .
.
Завдання № 11. Знайти екстремум функції  .
.
Розв’язання.
Знаходимо стаціонарні точки.

Рішення останньої системи дає 4 стаціонарні точки:
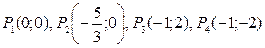 .
.
Знаходимо частинні похідні другого порядку:

Досліджуємо кожну стаціонарну точку.
1) у точці  Так як
Так як  і
і  , то у цієї точці функція має мінімум.
, то у цієї точці функція має мінімум.

2) у точці  Так як
Так як  і
і  , то у цієї точці функція має максимум.
, то у цієї точці функція має максимум.

3) у точці  Так як
Так як 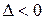 , то у цієї точці функція екстремума не має.
, то у цієї точці функція екстремума не має.
4) у точці 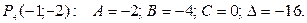 Так як
Так як 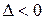 , то у цієї точці функція екстремума не має.
, то у цієї точці функція екстремума не має.
Рекомендована література
1. Письменный, Д.Т. Конспект лекций по высшей математике. В 2 ч. Ч. 1 / Д.Т. Письменный. –М.: Айрис-пресс, 2003. – 288 с.
2. Щипачев, В.С. Высшая математика: учебник для вузов / В.С. Щипачев.– М.: Высш. шк., 1998.– 479 с.
3. Данко, П.Е. Высшая математика в упражнениях и задачах. В 2 ч. Ч.1 / П. Е. Данко, А.Г. Попов, Т.Я. Кожевникова.– М.: Высш. шк., 1999.– 304 с.
4. Щипачев, В.С. Задачник по высшей математике / В.С. Щипачев.– М.: Высш. шк., 2001.– 304 с.
по электронной почте: pr-com@usue.ru.
|
|
|
|
Дата добавления: 2017-01-14; Просмотров: 104; Нарушение авторских прав?; Мы поможем в написании вашей работы!