Механические характеристики материала

Все материалы под нагрузкой деформируются, т. е. меняют форму и размеры. Характер деформации можно проследить при испытании материалов на растяжение или сжатие.

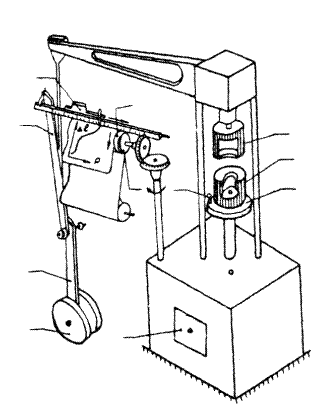
Перед испытанием на растяжение цилиндрический образец закрепляется в захватах разрывной машины, растягивается и доводится до разрушения. При этом фиксируется зависимость между приложенным усилием и деформацией. Получают график, называемый диаграммой растяжения.

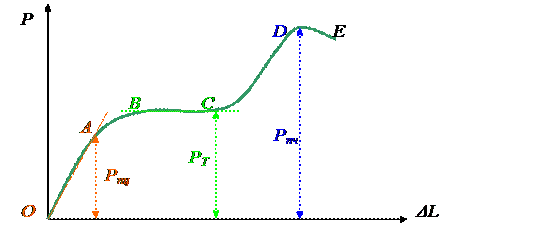
Примерный вид диаграммы для малоуглеродистых сталей, записанной машиной в процессе испытания, представлен на рисунке.

ОА – упругая стадия. На большей части своего протяжения участок прямолинеен. В этой части диаграмма выражает прямую пропорциональную зависимость между силой и деформацией, то есть зависимость, записываемую законом Р. Гука. Ордината точки A в масштабе диаграммы равна наибольшей нагрузке обозначаемой Р_пц, при которой выполняется закон Гука.

Предел пропорциональности − наибольшее напряжение σ_пц, превышение которого вызывает отклонение от закона Гука. Предел пропорциональности определяется по формуле:

где A ₀ – начальная площадь поперечного сечения образца.

После прекращения нагрузки никаких остаточных деформации нет.

АВ – После перехода через предел пропорциональности деформации начинают интенсивно нарастать. В дальнейшем рост нагрузки замедляется и вскоре совсем прекращается.

ВС – площадка текучести. Деформации растут без дальнейшего увеличения нагрузки − материал образца «течет». На диаграмме при этом прочерчивается горизонтальная линия. Явление роста деформаций при постоянной нагрузке называется текучестью. Ординаты точек на этом участке устанавливают нагрузку Р_Т, с учетом которой вычисляется предел текучести σ _Т.

Предел текучести − напряжение, при котором происходит «течение» материала, то есть рост деформации при постоянной (примерно) нагрузке. Он определяется по формуле:

Для ряда высокоуглеродистых и легированных сталей, сплавов цветных металлов площадки текучести может и не быть. В этом случае за величину предела текучести условно принимают напряжение, при котором остаточное удлинение образца составляет 0,2%. Условный предел текучести обозначается σ₀₂.

СD – упрочнение. После окончания стадии текучести образец снова начинает сопротивляться деформациям.

На этом участке от конца участка «текучести» до максимума кривой в точке D наблюдается некоторое увеличение нагрузки на образец. Если повторно нагрузить образец исчезает участок текучести, образец приобретает способность воспринимать без остаточных деформаций большие нагрузки. Это явление в технике называется «наклепом» или упрочнением материала образца. Наклеп – это явление увеличения упругих свойств в результате предварительного пластического деформирования.

В точке D кривая имеет наибольшую ординату. Эта ордината в масштабе диаграммы равна максимальной нагрузке, обозначаемой Р_пч, при которой материал образца начинает претерпевать разрушение.

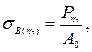Предел прочности или временное сопротивление − это напряжение, при котором происходит разрушение материала. Предел прочности σ_{в (пч)} находится как отношение максимальной силы, которую способен выдержать образец при растяжении, к его начальной площади поперечного сечения, то есть:

Следует отметить, что предел пропорциональности, предел текучести и предел прочности являются условными характеристиками, так как соответствующие им нагрузки относятся к начальной площади А ₀.

DЕ – разрушение. После достижения максимальной нагрузки в точке D наблюдается качественное изменение характера деформаций. Деформация образца начинает концентрироваться около какого-либо участка по длине образца, оказавшегося наиболее слабым. На образце образуется прогрессирующая «шейка».

Вследствие интенсивного уменьшения площади сечения «шейки» для дальнейшего растяжения образца нужна меньшая нагрузка. Поэтому на диаграмме наблюдается снижение нагрузки, продолжающееся до разрыва образца. В точке Е кривая диаграммы вследствие разрыва образца обрывается. Нагрузка, соответствующая моменту разрыва образца, называется разрушающей и обозначается Р_разр. Разделив нагрузку Р_разр на А_ш − площадь сечения в месте разрушения образца, получим величину истинного напряжения разрушения образца:

Истинное напряжение − это напряжение, при котором происходит разрыв образца.

Чтобы избежать влияния размеров образца принято строить диаграмму σ = f (ε). При этом рассчитываются величины, имеющие условный характер, усилия в каждой из точек делят на величину начальной площади поперечного сечения, хотя в каждый момент идет деформация, и площадь образца уменьшается. Такая диаграмма растяжения не зависит от абсолютных размеров образца.

σ_пц – предел пропорциональности – наибольшие напряжения, до которых справедлив закон Гука (для стали 200 МПа).

σ_упр – предел упругости – наибольшие напряжения, до которых материал не имеет остаточных деформаций (для стали 200 МПа).

σ_Т – предел текучести – напряжение, при которых происходит рост деформаций без увеличения нагрузки (для стали 240 МПа).

σ_B – предел прочности или временное сопротивление – напряжение, которые может выдержать образец без разрушения (для стали 400 МПа).

Для оценки качества испытанной стали необходимо определить количество работы, затраченной на разрыв образца. Чем больше работы необходимо затратить на разрыв образца, тем больше энергии в состоянии поглотить материал, не разрушаясь, тем лучше он будет сопротивляться ударным нагрузкам, поглощая кинетическую энергию удара.

Работа, затраченная на разрушение образца, соответствует площади диаграммы растяжения О − A − B − C − D − E − F (с учетом масштаба сил и деформации). Чтобы получить величину, характеризующую сопротивление материалов образца разрыву, необходимо подсчитать удельную работу растяжения, т.е. есть количество работы, приходящейся на единицу объема:

где a – работа, затраченная на разрушение образца,

a_уд – удельная работа,

V₀ – начальный объем образца.

Практически величину работы a можно определить по формуле

a = η ∙ P _max ∙ Δ L _ост,

где η – коэффициент полноты диаграммы, учитывающий отличие площади параллелограмма O − A ₁− E ₁− F от действительной площади диаграммы.

Коэффициент полноты диаграммы в зависимости от марки стали примерно равен η = 0,8 ÷ 0,9.

Для стали, кроме того, определяются показатели пластичности:

а) Остаточное относительное удлинение

б) Относительное остаточное поперечное сужение

L ₀ – длина образца до испытания,

L ₁ – длина образца после разрыва,

A ₀ – площадь поперечного сечения образца до испытания,

A _ш – площадь поперечного сечения в месте разрыва образца,

Характеристики пластичности определяют способность материала к деформированию, чем выше значения δ и Ψ, тем материал пластичнее.

В зависимости от δ материалы делятся на пластичные δ > 5% (углеродная сталь, медь, алюминий) и хрупкие δ < 5% (чугун, бетон, инструментальная сталь).

Диаграмма растяжения хрупких материалов не имеет площадки текучести. Для них проводят испытание на сжатие, так как они лучше оказывают сопротивление сжатию, чем растяжения (Для пластичных материалов модуль упругости, предел упругости, предел текучести при растяжении и сжатии приблизительно одинаковы).

Кроме хрупких и пластичных материалов существуют еще упруго- вязкие материалы (полиамиды). Для них характерно явление ползучести и релаксации напряжений.

Ползучесть – это непрерывный рост пластических деформаций при неизменной нагрузке.

Релаксация напряжений – медленное уменьшение напряжений при неизменной полной деформации за счет увеличения пластической составляющей и уменьшения упругости.

Таким образом, материалы принято делить по типу их диаграмм растяжения на три группы.

К первой группе относят пластичные материалы, эти материалы имеют на диаграмме растяжения площадку текучести (диаграммы первого типа).

Ко второй группе относятся хрупкие материалы, эти материалы мало деформируются, разрушаются по хрупкому типу. На диаграмме нет площадки текучести.

К третьей группе относят материалы, не имеющие площадки текучести, но значительно деформирующиеся под нагрузкой, их называют пластично-хрупкими. Пластично-хрупкие материалы значительно деформируются, этого нельзя допустить в работающей конструкции. Поэтому их деформации обычно ограничивают. Максимально возможная относительная деформация ε = 0,2%.

Действительная диаграмма используемой в строительстве стали Ст3 часто заменяется приближенно условной диаграммой, состоящей из наклонного и горизонтальных участков.

Такая диаграмма носит название диаграммы идеально упруго-пластического тела или диаграммы Прандтля. Расчет по диаграмме Прандтля имеет свои особенности и называется расчетом по методу предельного равновесия. Этот расчет дает возможность находить предельную несущую способность системы, при которой все элементы остаются целыми, но система уже не может воспринимать дальнейшее приращение нагрузки.

Стали с повышенным содержанием углерода и легированные допускают меньшие пластические деформации до разрушения, поэтому для строительных конструкций они не применяются.

Бетон с самого начала нагружения имеет криволинейную диаграмму работы на сжатие и почти не работает на растяжение.

Железобетонные стержни благодаря наличию в них арматуры сравнительно хорошо работают на растяжение.

Дерево при растяжении вдоль волокон подчиняется закону Гука, но разрушается хрупко. На сжатие оно следует криволинейной диаграмме работы, которая с известной точностью может быть заменена диаграммой Прандтля. Несмотря на то, что временное сопротивление древесины на растяжение больше, чем на сжатие, в строительных конструкциях избегают растянутых деревянных элементов. Они опасны из-за хрупкого характера разрушения.

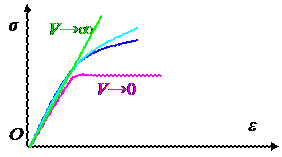Расчет по фактической диаграмме тоже не является вполне точным и строгим, так как сама диаграмма не является постоянной характеристикой материала, а зависит от режима нагружения: при большой скорости нагружения V она приближается к прямой линии закона Гука, при малой скорости – показывает большой рост пластических деформаций.

Таким образом, в зависимость напряжений от деформаций входит фактор времени. Раскрытие этих зависимостей приводит к уравнениям ползучести, которые имеют вид уже не функций, а дифференциальных или интегральных соотношений.

Наиболее хорошо разработаны методы расчета конструкций из упругих материалов, т. Е. подчиняющихся закону Гука. Эти методы широко применяются в качестве приближенных и для материалов со слабо криволинейной диаграммой при не слишком больших напряжениях.

Дата добавления: 2017-01-14