Знать определения (уметь также распознавать их среди предложенного набора высказываний), уметь приводить примеры, удовлетворяющие и не удовлетворяющие определениям

Дополнительная часть (знать формулировки теорем и указанные доказательства)

16. Теорема о пределе монотонной ограниченной последовательности.

17. Число e (с доказательством).

18. Принцип вложенных отрезков (с доказательством).

19. Теорема Больцано-Вейерштрасса (с доказательством).

20. Теорема существования точных граней.

21. Критерий Коши сходимости последовательности (с доказательством).

22. Критерий Коши существования предела функции.

23. Свойства функций, непрерывных на отрезке: ограниченность (с доказательством), достижение наибольших и наименьших значений.

24. Теоремы об обращении функции в ноль (с доказательством) и о промежуточном значении.

25. Понятие равномерной непрерывности. Теорема Кантора.

26. Понятие обратной функции. Теорема существования обратной функции.

БАЗОВЫЙ УРОВЕНЬ К КОЛЛОКВИУМУ ПО МАТЕМАТИЧЕСКОМУ АНАЛИЗУ

(ЭКТ-1, 1 семестр) 2011/12 гг.

Уметь распознавать:

1.1. Сходящиеся и расходящиеся последовательности.

1.2. Ограниченные и неограниченные последовательности.

1.3. Монотонные последовательности.

1.4. Бесконечно малые и бесконечно большие последовательности.

1.5. Точки разрыва, непрерывности функций.

1.6. Эквивалентные функции

2.1. Ограниченных последовательностей (включая ограниченные сверху и снизу).

2.2. Возрастающих, убывающих, невозрастающих, неубывающих последовательностей.

2.3. Предела последовательности (на ε-n языке, на языке окрестностей)

2.4. Бесконечно малые и бесконечно большие последовательности.

2.5. Предела функции в точке (все 16 случаев) по Коши и по Гейне.

2.6. Непрерывности функции в точке, на интервале, отрезке.

2.7. Точек разрыва: устранимых, 1 рода, 2 рода.

2.8. Эквивалентных функций, порядка малости одной функции относительно другой, о-малого.

2.9. Односторонних пределов.

2.10. Знать замечательные пределы и следствия из них.

2.11. Точных граней.

Знать свойства (уметь формулировать соответствующие утверждения)

3.1. Сходящихся последовательностей: единственность предела, ограниченность, переход к пределу в неравенствах, сохранение знака предела.

3.2 Арифметические операции над последовательностями, имеющими предел.

3.3 Бесконечно малых и бесконечно больших последовательностей.

3.4 Основных элементарные функции и их графики.

3.5 Свойства функций, имеющих предел в точке (локальная ограниченность, сохранение знака, переход к пределу в неравенствах, арифметические свойства).

3.6 Свойства функций, непрерывных в точке.

Примерный вариант билета для коллоквиума (ЭКТ-1, 1 семестр, 2011/12)

1. Дать определение точной нижней грани множества.

2. Сформулировать определение по Коши и по Гейне: .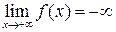

3. Функция : свойства, график.

4. Сформулировать и доказать свойство о пределе произведения сходящихся последовательностей.

Дополнительный

5. Число e (с доказательством)

Примерные критерии оценок:

Удовлетворительно – зачтены ответы на вопросы 1-4 (без доказательства свойства)

Хорошо – зачтены ответы на вопросы 1-4 (с доказательством свойства)

Отлично – зачтены ответы на вопросы 1-5

Дата добавления: 2017-01-14