
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Определители произвольного порядка
|
|
|
|
Каждой квадратной матрице  можно поставить в соответствие определенное число, называемое ее определителем и обозначаемое символом
можно поставить в соответствие определенное число, называемое ее определителем и обозначаемое символом  или в развернутом виде:
или в развернутом виде:
 .
.
Числа  называют элементами определителя.
называют элементами определителя.
Минором элемента  называется определитель, полученный из исходного, путем вычеркивания строки и столбца, на пересечении которых стоит элемент
называется определитель, полученный из исходного, путем вычеркивания строки и столбца, на пересечении которых стоит элемент  . Минор элемента
. Минор элемента  обозначается
обозначается 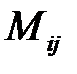 .
.
Определителем порядка  называют сумму произведений элементов первой строки на их соответствующие миноры
называют сумму произведений элементов первой строки на их соответствующие миноры
 (4.1).
(4.1).
Величину  называют алгебраическим дополнением элемента
называют алгебраическим дополнением элемента  . Справедливо равенство
. Справедливо равенство
 (4.2).
(4.2).
Равенство (4.2) называют разложением определителя по  -ому столбцу или по
-ому столбцу или по  -ой строке.
-ой строке.
Квадратная матрица называется невырожденной, если ее определитель не равен нулю. В противном случае матрица называется вырожденной.
Справедливо утверждение: всякая невырожденная матрица  имеет обратную матрицу
имеет обратную матрицу  .
.
Обратную матрицу находят по формуле: 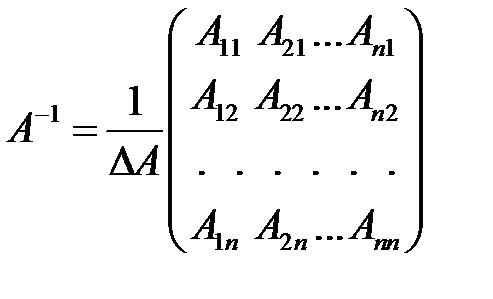 , где
, где  - алгебраические дополнения элементов
- алгебраические дополнения элементов  матрицы
матрицы  , причем алгебраические дополнения элементов строки матрицы
, причем алгебраические дополнения элементов строки матрицы  записываются в соответствующий столбец матрицы
записываются в соответствующий столбец матрицы  .
.
Пример 8. Найти обратную матрицу  матрицы
матрицы  и сделать проверку.
и сделать проверку.
Решение. Вычислим определитель матрицы  :
:
 .
.
Найдем алгебраические дополнения:

Запишем обратную матрицу:
 .
.
Сделаем проверку. Найдем  .
.

|
|
|
|
|
Дата добавления: 2017-01-14; Просмотров: 138; Нарушение авторских прав?; Мы поможем в написании вашей работы!