Додавання гармонічних коливань однакового напрямку і однакової частоти. Биття

Перш ніж розглядати додавання ко­ливальних рухів, спинимось на способі
зображення коливань за допомогою обертального вектора амплітуди.

Для цього із довільної точки О, яка вибрана на осі X, під кутом , що дорівнює початковій фазі коливань, відкладемо вектор , модуль якого дорівнює амплітуді A коливання (рис. 28).

Проекція вектора 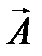на вісь OX дорівнює зміщенню 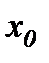у момент початку відліку часу :

.

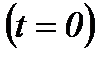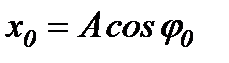Обертатимемо вектор амплітуди навколо осі O, яка перпендикулярна до площини рисунка, з кутовою швидкістю . За проміжок часу t вектор амплітуди повертається на кут 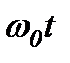. Проекція вектора 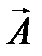в цьому положенні на вісь ОХ дорівнює:

.

За час Т, що дорівнює періоду коли­вань, вектор амплітуди повертається на кут 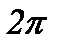, а проекція його кінця зробить одне повне коливання навколо положення рівноваги O, отже, обертовий вектор амплітуди повністю характеризує гармонічне коливання.

Нехай точка бере участь у двох гар­монічних коливаннях однакової частоти, які напрямлені вздовж однієї прямої:

,

.

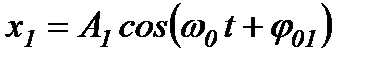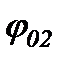Ці коливання зручно додати, користуючись методом обертального вектора амплітуди. Для цього відкладемо з точки О під кутом вектор амплітуди , а під кутом - вектор амплітуди (рис. 29).

Оскільки вектори і обертаються з однаковою кутовою швидкістю, то різниця фаз 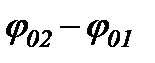між ними постійна. Оскільки сума проекцій двох векторів на одну вісь дорівнює проекції на ту саму вісь вектора, який є їх сумою, то результуюче коливання можна подати вектором амплітуди , що дорівнює сумі векторів і :

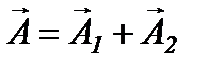
і який обертається навколо точки з тією самою кутовою швидкістю , що й вектори і . Результуюче коливання описуються рівнянням

,

де – амплітуда результуючого коливання, а – його початкова фаза.

Застосовуючи теорему косинусів до одного з трикутників, на які паралелограм розбивається діагоналлю, з рис. 29 видно, що

,

.

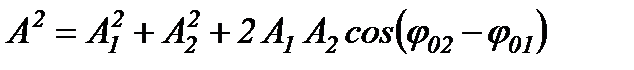Амплітуда A результуючого коли­вання залежить від різниці початкових фаз коливань, що додаються. Можливі значення A лежать в межах

.

Розглянемо кілька окремих випадків.

1). , .

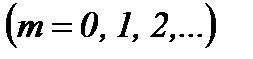Тод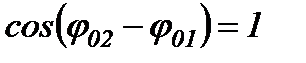і і .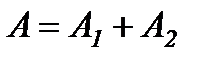

2). , .

Тод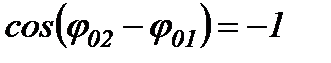і і .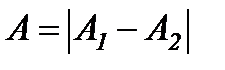

Розглянемо аналітичний метод знаходження результуючого коливання в дея­ких простих випадках:

а) частоти і фази коливань, що додаються, однакові, амплітуди різні:

.

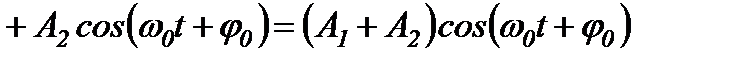Амплітуда результуючого коливання дорівнює сумі амплітуд коливань, що додаються.

б) частоти і амплітуди однакові, фази відрізняються на :

.

Амплітуда результуючого коливан­ня

менша суми амплітуд, що додаються; зокрема, якщ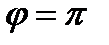о , то .

Якщо частоти коливань і 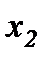неоднакові, то вектори і будуть обертатися з різною швидкістю. В цьому ви­падку результуючий вектор пульсує за величиною і обертається зі змінною швидкістю. Результуючим рухом буде в цьому випадку не гармонічне коливання, а деякий складний коливний процес.

Особливий інтерес становить випадок, коли два гармонічні коливання однакового напрямку, що додаються, мало відрізняються за частотою.

Періодичні зміни амплітуди коливання, які виникають при додаванні двох гармонічних коливань одного напрямку з близькими частотами, називаються бит­тями.

Нехай амплітуди коливань

, ,

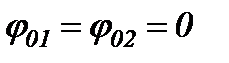а частоти дорівнюють

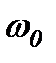, і << .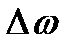

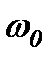Тоді рівняння коливань матимуть вигляд:

,

.

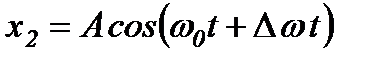Додаючи ці вирази і застосовуючи тригонометричну формулу для суми коси­нусів, отримуємо:

.

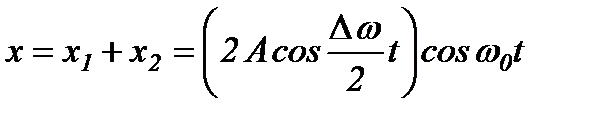Отриманий вираз є добуток двох коливань. Оскільки 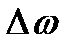<< 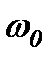, то множник майже не зміниться, коли множник здійснює кілька повних коливань. Тому результуюче коливання 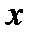можна розглядати як гармонічне з частотою 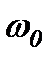й амплітудою

.

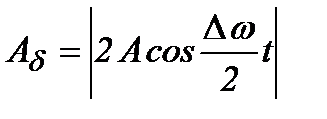Частота зміни удвоє більша від частоти зміни косинуса (оскільки береться за модулем). Частота биття дорівнює різниці частот коливань, що додаються, тобто . Період биття .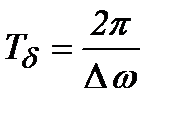

Суцільні лінії на рис. 30 дають графік результуючого коливання у випадку 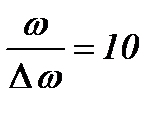, і графік амплітуди .

Дата добавления: 2015-07-13