Диференціальне рівняння згасаючих коливань і його розв’язання

Усі реальні коливальні системи є дисипативними. Енергія механічних коли­вань такої системи поступово витрачається на роботу проти сил опору, тому вільні коливання завжди згасаючі - їх амплітуда
поступово зменшується.

Для пружинного маятника масою m, що здійснює малі коливання під дією
пружної сили 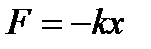, сила опору пропорційна до швидкості, тобто

, ,

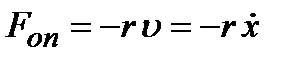де – коефіцієнт опору.

Другий закон Ньютона для згасаючих коливань має наступний вигляд:

,

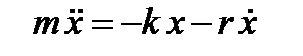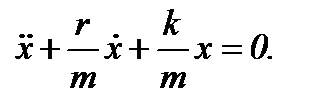
Введемо позначення

, ,

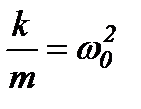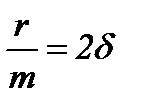де 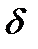– коефіцієнт згасання, а 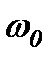– власна частота з якою здійснювались би вільні коливання за відсутності опору середовища.

Тоді другий закон Ньютона можна записати у вигляді

.

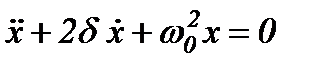Для розв’язання цього рівняння введемо нову змінну u, яка зв’язана з x співвідношенням . Звідси

,

.

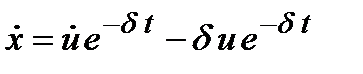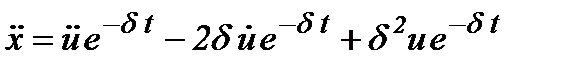Підставивши ці значення 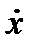і в рівняння другого закону Ньютона для зга­саючих коливань і скорочуючи всі доданки на множник 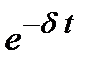, отримуємо

.

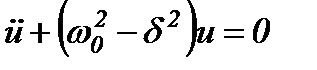Нехай опір середовища малий і 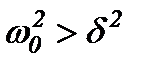. Тоді можна ввести позначення

.

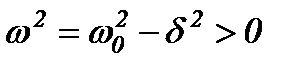В результаті отримуємо рівняння

,

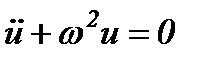розв’язок якого має такий вигляд

,

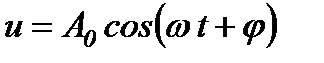де 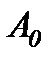і 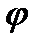– сталі, які визначаємо з початкових умов. Отже,

,

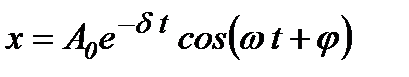де 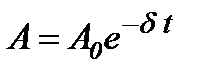- амплітуда загасаючих коливань, а 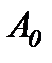- початкова амплітуда. Амплітуда згасаючих коливань зменшується з плином часу і тим скоріше, чим більший коефіцієнт опору і чим менша маса коливного тіла.

Величина 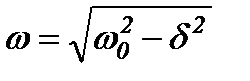називається власною циклічною частотою коливань дисипативної системи. Графік залежності x від часу наведений на рис. 36.

Згасаючі коливання – неперіодичні коливання, бо в них ніколи не повторюються, наприклад, максимальні значення змі­щення, швидкості і прискорення. Однак при згасаючих коливаннях величина x перетворюється в нуль, змінюючись в один і той самий бік, а також досягає максимальних і мінімальних значень через однакові проміжки часу:

.

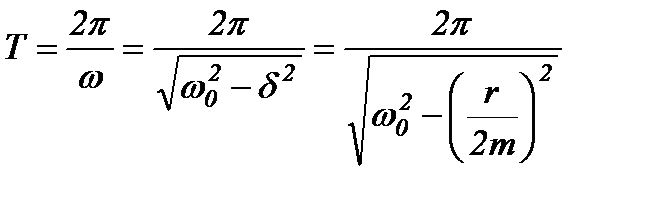Величину T тому називають періо­дом згасаючих коливань.

Якщо 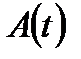і 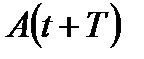– амплітуди двох послідовних коливань, що йдуть одне за одним через проміжок часу T, то відношення

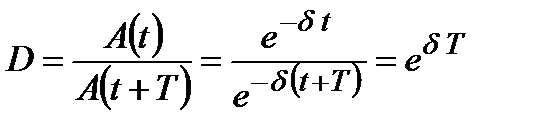
називається декрементом згасання, а його натуральний логарифм

æ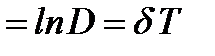

– логарифмічний декремент згасання.

Позначимо 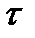проміжок часу, протягом якого амплітуда коливань зменшується в e разів. Тоді

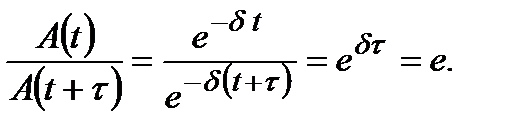
Звідси

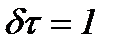, або .

Коефіцієнт згасання 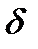є фізична величина, обернена до проміжку часу, протягом якого амплітуда зменшується в e разів. Час 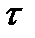називається часом релаксації.

Нехай N – кількість коливань, після яких амплітуда коливань зменшується в e разів. Тоді

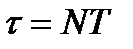, æ .

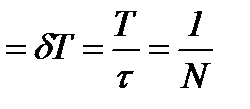Логарифмічний декремент згасання æ є фізична величина, обернена до кількос­ті коливань N, після закінчення яких амплітуда зменшується в e разів.

Добротністю коливальної системи називається величина 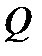, яка дорівнює добутку 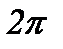на відношення енергії 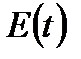коливальної системи в довільний момент часу t до зменшення цієї енергії за проміжок часу від t до t+T:

.

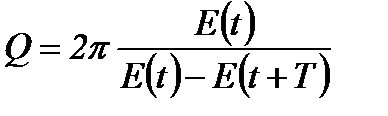Оскільки енергія 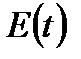пропорційна до квадрата амплітуди коливань, то

.

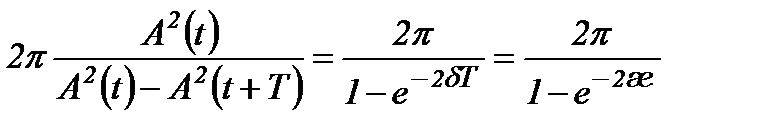При малих значеннях æ (æ <<1)

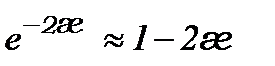
і

.

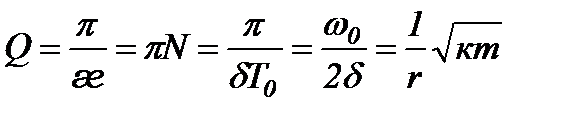Тут враховано, що при æ <<1 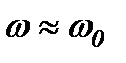і умовний період Т згасаючих коливань практично дорівнює періоду 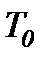вільних коливань.

Дата добавления: 2015-07-13