Наращивание и дисконтирование

Введение

Эффективная деятельность предприятий в долгосрочной перспективе, обес­печение высоких темпов развития, повышение конкурентоспособности в услови­ях рыночной экономики в значительной мере определяется уровнем их инвести­ционной активности и диапазона инвестиционной деятельности. Реализация инве­стиционных программ позволяет совершенствовать производство, улучшать каче­ство продукции, обеспечивает рост производительность труда и в конечном итоге - выживаемость и развитие предприятий в современных условиях. Вот почему так - важно правильно распорядиться имеющимися инвестиционными ресурсами, уметь выбрать лучший вариант осуществляемых вложений, рассчитать их эффек­тивность и прогнозировать последствия этих вложений. Любые решения в облас­ти инвестиций опираются на соответствующий аппарат количественной оценки целесообразности принятия того или иного инвестиционного проекта, формирования оптимальной инвестиционной программы.

Осуществление инвестиционной деятельности на предприятии требует определенных знаний теории, а также практических навыков в области инвестиро­вания.

Цель данной дисциплины - дать будущим специалистам знания, кото­рые будут использованы ими в практической деятельности при подготовке и принятию решений по комплексу вопросов, связанных с осуществлением ин­вестиционной деятельности

Задачи дисциплины дать:

• теоретические знания в области методологии и методики экономической оценки инвестиций;

• сформировать практические навыки проведения расчетов показателей экономической эффективности инвестиций и обоснования выбора альтернативных вариантов инвестиций;

• обеспечить обучение новейшим методологическим разработкам в области анализа, планирования и оценки инвестиций в условиях рыночной экономики.

В результате изучения дисциплины "Экономическая оценка инвести­ций" студент должен получить необходимые теоретические и практические знания, умения и навыки, а именно:

- иметь представления об экономическом содержании инвестиций, их ос­новных видах, источниках финансирования инвестиционной деятельности и основах экономической оценки инвестиций;

- знать:

• основные принципы и механизмы реализации инвестиционной политики государства;

• содержание и классификацию инвестиционных проектов, стадии их реа­лизации;

• основные принципы расчета и обоснования экономической оценки инве­стиций;

• основные методы оценки эффективности инвестиций.

Тема № 1 - Основы финансовой оценки денежных потоков:

Теоретическая часть

В процессе разработки инвестиционных проектов осуществляются различного рода финансово-экономические расчеты, связанные с потоками денежных средств в различные периоды времени. Ключевую роль в этих расчетах играет оценка стоимости денег во времени.

Необходимость учета фактора времени определяется принципом неравноценности денег, относящихся к разным периодам времени.

Концепция стоимости денег во времени состоит в том, что она с течением времени изменяется с учетом возможного получения дохода; в качестве последнего обычно выступает норма процента.

В практике применяются различные виды процентных ставок. Одно из основных их отличий связано с выбором исходной базы для начисления процен­тов. Ставки процентов, применяемые к одной и той же начальной сумме на про­тяжении всего срока ссуды, называются простыми процентными ставками, а к сумме с начисленными в предыдущем периоде процентами - сложными про­центными ставками.

Процентные ставки могут быть, в зависимости от их постоянства во време­ни: постоянными или переменными («плавающими»).

Концепция неравномерности потоков денежных средств, относящихся к разным моментам времени, является основой анализа экономической эффектив­ности таких операций. Используются два метода корректировки денежных пото­ков — метод наращивания капитала и метод дисконтирования.

Наращивание (компаундинг) - это процесс увеличения первоначальной суммы денежных средств в результате начисления процентов. Используя метод наращивания можно определить величину денежных средств через некоторый пе­риод времени - ее будущею стоимость (S).

наращивание

Первоначальная сумма Будущая стоимость

Наиболее простыми видами долгосрочных финансовых операций являются разовые платежи (выдача и погашение кредита и депозита).

Процесс наращивания с начислениями описывается арифметической про­грессией, и определяется по формуле:

S = P(1+n*i) (1)

где S – наращенная сумма денежных средств;

P – первоначальная сумма денежных средств;

n – период времени;

i – ставка процента.

Практика начисления простых процентов. Начисление простых процен­тов обычно используется в двух случаях: 1) при заключении краткосрочных кон­трактов (предоставление краткосрочных кредитов и т. д.), срок которых не пре­вышает года (n <= 1); 2) когда проценты не присоединяются к сумме долга, а пе­риодически выплачиваются.

При дискретно изменяющихся во времени процентных ставках показатель (коэффициент) наращивания определяется по формуле:

(2)

где it - ставка простых процентов в периоде t;

nt — продолжительность t — периода начисления процентов;

it — величина ставки процента в каждом интервале.

Если же продолжительность периода начисления процентов не равномерна, то можно использовать следующую форму расчета коэффициента наращивания:

(3)

где - величина каждого последующего интервала во времени.

Процесс обратный наращиванию называется дисконтированием.

Дисконтирование представляет собой метод нахождения величины денеж­ной суммы в данный момент времени, получение или выплата которой планиру­ется в будущем.

дисконтирование

Первоначальная сумма Будущая стоимость

Дисконтирование осуществляется по следующему выражению:

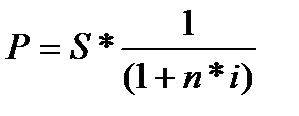(4)

где Р — текущая (современная) стоимость денежных средств;

Дробь в правой части равенства при величине S называется дисконтным множителем. Этот множитель показывает, какую долю составляет первоначаль­ная сумка ссуды в окончательной величине долга.

Сложные проценты применяются в долгосрочных финансовых операциях, если проценты не выплачиваются сразу после их начисления за прошедший ин­тервал времени, а присоединяются к сумме долга. Присоединение начисленных процентов к сумме долга часто называют капитализацией процентов.

Формула наращивания по сложным процентам:

(5)

где - множитель наращивания.

В практических расчетах в основном применяют дискретные проценты, т.е. проценты, начисляемые за одинаковые интервалы времени (год, полугодие, ме­сяц, и т.д.).

Как ранее указывалось, начисление процентов может производиться чаще, чем за один год, - по полугодиям, кварталам и т.д. В подобных случаях для расче­та наращенной суммы можно использовать формулу наращивания, в которой n - число периодов начисления процентов, a i - ставка процента за соответствующий период.

Однако в большинстве случаев используется номинальная ставка (j)

Начисление процентов по номинальной ставке производится по формуле:

(6)

где j - номинальная годовая процентная ставка;

m - число периодов начисления процентов в году;

n - число лет;

Р - число периодов начисления процентов за весь срок контракта.

Кроме номинальной ставки существует эффективная процентная ставка. Она измеряет тот относительный доход, который получает владелец капитала в целом за год и определяется по формуле:

(7)

В том случае, когда ставка сложных процентов меняется во времени, фор­мула коэффициента наращивания имеет вид:

(8)

где i1, i2, …, ir – процентные ставки по периодам;

n1, n2, …, nr – периоды начисления.

При дробном числе лет процент начисляется различными способами:

1) по формуле сложных процентов:

(9)

где t - дробная часть года

2) на основе смешанного метода, в соответствии с которым за целое число лет начисляются сложные проценты, а за дробное - простые проценты.

(10)

Дисконтирование или процесс нахождения текущей стоимости по сложным процентам производится по формуле:

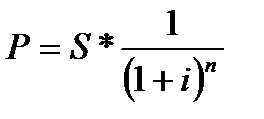(11),

где - дисконтный множитель.

При начислении процентов за m периодов в году расчет текущей стоимости можно производить по предыдущей формуле (31) или по формуле:

(12)

Очень часто в договорах финансового характера предусматриваются не отдельные разовые платежи, а серия платежей, распределенных во времени (напри­мер, регулярные выплаты с целью погашения долгосрочного кредита вместе с начисленными на него процентами; периодические взносы на расчетный счет, на котором формируется некоторый фонд целевого назначения; дивиденды, выпла­чиваемые по ценным бумагам и проч.). Ряд последовательных платежей и посту­плений называют потоками платежей.

Наращенная сумма потока платежей это сумма всех последовательных платежей, с начисленными на них процентами, к концу срока ренты.

Под современной величиной потока платежей понимают сумму всех платежей, дисконтированных на некоторый момент времени, совпадающий с на­чалом потока платежей или предшествующий ему.

Таким образом, современная стоимость на конец срока является эквива­лентной суммой, выплачиваемой за один период платежа до даты первой выпла­ты. Будущая стоимость является эквивалентной суммой на момент последнего платежа.

Потоки платежей, производимых через равные промежутки времени, назы­вают финансовой рентой или аннуитетом.

Период времени между двумя последовательными платежами называется ин­тервалом (периодом) платежа (ренты).

Сроком аннуитета (ренты) является время от начала первого до конца по­следнего интервала платежа.

Наращенная сумма потока платежей в целом определяется следующим об­разом:

(13)

где R_t - ряд платежей, выплачиваемых в течении определенного периода;

n - общий срок выплат;

nt - время выплат рент после некоторого начального периода.

Современная стоимость такого платежа определяется как:

(14)

где -дисконтный множитель по ставке i

(15)

Обычная годовая рента наращивания суммы рассчитывается так:

(16)

где R - годовая сумма платежей.

Обычная годовая рента текущей величины рассчитывается как:

(17)

где А - современная (текущая) величина ренты.

Примеры решения задач.

Пример 1. Предприятием взята ссуда в размере 100 тыс. руб., срок долга 11 месяцев. Определить сумму накопленного долга по ставке простых процентов, равной 30 % годовых. Используя формулу (1) получим:

S = 100 000 * (1 + 0,9 * 0,3) = 127 000 тыс. руб.

Пример 2. Договором предусматривается получение ссуды в размере 50 тыс. руб. на 1 год с ежеквартальным начислением процентов. За первый квартал раз­мер процента - 10% годовых, а за каждый последующий на 1% выше, чем преды­дущий. Необходимо определить суммы выплат по ссуде.

Для этого определяем коэффициент наращивания за весь срок договора по формуле (2):

а = 1+0,25*0,1+0,25*0,11+0,25*0,12+0,25*0,13=1,115

Отсюда будущая сумма выплат по ссуде составит

S = P*a = 50* 1,1 15 = 55,75 тыс. руб.

Пример 3. Организация получила ссуду на 2,5 года в размере 400 тыс.руб. под простые проценты. Договор предусматривает следующую схему начисления простых процентов: за первый год 20%, в следующее полугодие — 22%, в каждом последующем квартале ставка повышается на 3%. Требуется определить нара­щенное значение долга.

В соответствии с формулой 3 определяем коэффициент наращивания:

а=1+1*0,20+0,25*0,25+0,25*0,28+0,25*0,31+0,25*0,34+0,5*0,22=1,605 Следовательно, наращенное значение долга составит:

S= 400*1,605=642 тыс.руб.

Пример 4. Определить какую сумму необходимо положить на депозитный счет в банке, чтобы получить через 6 месяцев 50 тыс. руб., при начислении про­стых процентов в размере 20 %.

Р = 50000* 17(1+0.5*0.2) = 50 000/1.1 =45.5 тыс. руб.

Пример 5. Средства в размере 50 000 руб. вложены на 3 года под 10% годо­вых; начисление процентов производится ежеквартально. Определить наращен­ную сумму денег.

Пример 6. Определить эффективную ставку сложных процентов с тем, чтобы получить такую же наращенную сумму, как и при использовании номинальной ставки j=20 %, при ежемесячном начислении процентов (m=12):

Пример 7. Найти наращенное значение долга по ссуде, выданной в размере 80 тыс. руб., если процентная ставка по ней в первый год составила 28%, а во вто­рой 30%.

В соответствии с формулой (8) коэффициент наращивания равен:

а= (1+0,28)¹*(1+0,3)²=1,664

отсюда наращенная сумма долга составит:

S=80*2,16=133,2 тыс.руб.

Пример 8. Организации в банке предложили (предоставили) ссуду в размере 400 тыс. руб. на 28 месяцев под 30% годовых на условиях годового начисления процента. Необходимо определить будущую стоимость ссуды.

В соответствии с первой схемой будущая стоимость равна:

S=400(l+0,3)²*(l+0,3*0,33)=742,92 тыс.руб.

По второй схеме

S = 400(1+0,3)^2,33=737,14 тыс. руб.

Пример 9. Определить современную (текущую) величину 100 тыс. руб. кото­рые должно получить предприятия через 3 года с момента инвестирования, исхо­дя из ставки 10% годовых.

Р= 100000*(1 + 0.1)^-3 =75,0 тыс. руб.

Пример10. Предприятие сдает в аренду помещение сроком на 3 года. Аренд­ные платежи в размере 40 тыс. руб. вносятся арендатором ежегодно в конце года в банк на счет предприятия. Банк на внесенную сумму начисляет проценты из рас­чета 20 % годовых. Определить сумму, полбенную предприятием в конце срока аренды при условии, что деньги со счета не изымались.

Используя формулу 16 для определения наращенной сум­мы, получим, что через 3 года сумма всех арендных платежей, помещенных в банк, составит:

Пример 11. Предприятие планирует через 3 года проинвестировать проект, стоимостью 300 тыс. руб.; для этого оно создает соответствующий фонд (пред­приятие имеет возможность ассигновать на эти цели ежегодно 82.4 тыс. руб., по­мещая их в банк под 20% годовых). Какая сумма потребовалась бы предприятию для создания фонда в 300 тыс. руб., ели бы оно поместило ее в банк одномомент­но на 3 года под 20% годовых.

Воспользуемся формулой для расчета современной (текущей) величины ренты и получим следующий результат:

Задания и задачи

Задача 1

Определить сумму накопленного долга, если ссуда равна 100 000 руб., срок долга 1,5 года при ставке простых процентов, равной 15% годовых.

Задача 2

Сумма в размере 50 000 руб. внесена в банк на 5 лет под 10% годовых, начисление производится ежеквартально. Определить наращенную сумму (при использовании сложных процентов).

Задача 3

Определить эффективную ставку сложных процентов с тем, чтобы получить наращенную сумму, если проценты начисляются ежеквартально, исходя из номинальной ставки 25% годовых. При этом внесён вклад в размере 50 000 руб. на четыре года.

Задача 4

Определить современную (текущую) сумму 300 000 руб., которые будут получены через четыре периода, при условии, что стоимость использования денег 15% годовых.

Задача 5

Определить какую сумму необходимо вложить, чтобы через 5 лет получить 400 000 руб., при ставке:

а) 20% годовых;

б) 3% ежемесячно.

Задача 6

В течение 5 лет на расчётный счёт в конце каждого года поступает по 10 млн. руб., на которые начисляют сложные проценты по:

а) годовой ставке – 20%;

б) ежеквартальной ставке – 4%;

Требуется определить сумму на расчётном счёте к концу указанного периода.

Задача 7

Компания АВС будет получать по 20 млн. руб. в год в течение 4 периода. Процентная ставка 10% годовых. Вычислить текущую стоимость денег.

Задача 8

Предположим, что стоимость денег 10% годовых. Мы можем заплатить долг, при этом у нас есть выбор: заплатить 10 000 руб. сегодня, или заплатить сумму Х через 5 лет. Чему равна максимальная величина Х, чтобы нам было выгодно платежи по ней отсрочить на 5 лет.

Задача 9

Организация получила ссуду на 3 года в размере 600 тыс. руб. под простые проценты. Договор предусматривает следующую схему начисления простых процентов: за первый год 25%, в каждом последующем квартале ставка повышается на 1%. Требуется определить наращенное значение долга.

Задача 10

Организации в банке предложили ссуду в размере 500 тыс. руб. на 36 месяцев под 24% годовых на условиях годового начисления процента. Необходимо определить будущую стоимость ссуды.

Задача 11

Компания создаёт фонд путём помещения в банк суммы в размере 2 млн. руб. Взносы в банк производятся по схеме обычного аннуитета (ренты):

а) ежеквартально, проценты банком начисляются один раз в год;

б) ежеквартально, проценты банком также начисляются ежеквартально;

Определить величину фонда в конце третьего года, при условии, что банк проценты начисляет по ставке 18% годовых.

Задача 12

Организация планирует создание в течение 5 лет фонда накопления в размере 300 тыс. руб. На эти цели ежегодно необходимо отчислять сумму в размере 40,3 тыс. руб. Какая сумма потребовалась бы организации на создание фонда в 300 тыс. руб., если она поместила их в банк на пять лет под 20% годовых с ежеквартальным начислением процентов на рентные платежи.

Задача 13

Необходимо определить наращенную сумму платежей за весь период ренты и современную стоимость потока платежей на начало срока при условии, что первоначальный платёж составит 100 тыс. руб. под 30% годовых, который с каждым кварталом увеличивается на 10%; срок ренты постнумерандо – 10 лет.

Задача 14

Банк "Империал" согласился ссудить компании "Чистый воздух" 300 тыс. руб. в ответ на обещание вернуть через 5 лет 750 тыс. руб. Какую годовую процентную ставку установил банк для компании.

Контрольные вопросы

1. Концепция временной ценности денежных средств.

2. Операции дисконтирования и наращивания капитала.

3. Формулы расчета текущей и будущей стоимости денежных средств.

4. Эффективная годовая процентная ставка

5. Понятие и виды аннуитетов.

6. Формулы расчета текущей и будущей стоимости аннуитета.

Список литературы

1. Анышин В.М. Инвестиционный анализ. – М.: Дело, 2004. – 280с.

2. Ендовицкий Д.А., Инвестиционный анализ в реальном секторе экономики. -М.: Финансы и статистика, 2007. – 352с.

3. Г.С. Староверова, А.Ю. Медведев, И.В. Сорокина. Экономическая оценка инвестиций. Учебное пособие. - М.: КноРус, 2010. - 312с.

Тема № 2 - Анализ и оценка денежных по­токов инвестиционного

Дата добавления: 2017-01-14