Статистическая обработка результатов. В любом аналитическом определении можно выделить три этапа: отбор пробы, проведение анализа, статистическая обработка результатов

Погрешности

В любом аналитическом определении можно выделить три этапа: отбор пробы, проведение анализа, статистическая обработка результатов.

Анализ включает много различных операций: физических, химических, математических. Так методика определения Ca в известняке предусматривает: отвешивание, перенесение в стакан, растворение в кислоте, нагревание, осаждение, нейтрализацию, отстаивание, отделение осадка фильтрованием, промывку, сушку осадка, перенесение в тигель, сжигание до весовой формы, охлаждение тигля, взвешивание, вычисление результатов (примерно 15 операций).

Даже при всей тщательности выполнения анализа найденный результат всегда в большей или меньшей степени отличается от истинного. Различают абсолютные и относительные систематические и случайные погрешности.

Абсолютная погрешность – отклонение результата измерения x_i от истинного значения x₀ измеряемой величины:

Δx_i= x_i–x₀,

имеет те же единицы измерения, что и x_i.

Относительная погрешность – отношение абсолютной погрешности к истинному значению

,

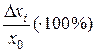безразмерная величина, выраженная в долях единицы или процентах.

Систематическая погрешность – та, которая при повторных измерениях остается постоянной или закономерно изменяется. Является следствием эффектов, которые не распознаны или не учтены. Источники: приборы, метод, реактивы, исследователь, посуда. Систематическую погрешность в принципе можно измерить и учесть. Она не меняется от опыта к опыту (результат всегда завышен или занижен).

Случайная погрешность – та, которая при повторном измерении изменяется случайным образом. Знак ее меняется. Случайные погрешности рассматриваются как случайные события и могут быть обработаны на основе теории вероятности и математической статистики.

Грубые погрешности (промахи) – существенно превышающие ожидаемые при данных условиях (потеря раствора при фильтровании, осадка при прокаливании и т.д.).

Правильность измерения – качество измерения, отражающее близость к нулю систематической погрешности. Статистическая обработка не показывает правильность;

Воспроизводимость измерений – качество измерений, отражающее близость друг к другу результатов, выполняемых в различных условиях; степень рассеивания результатов вокруг некоторого среднего значения.

Точность измерений – качество измерений, отражающее близость их результатов к истинному значению измеряемой величины.

Имеет две задачи:

1. Представить результаты многих определений в компактной форме – свертывание информации.

2. Оценить надежность результатов – степень их соответствия истинному содержанию элемента.

Случайные ошибки появляются по определенным законам, которые отражены в кривой нормального распределения Гаусса.

Практически вместо нормального распределения Гаусса

используют t-распределение Стьюдента, справедливое для малого объема выборки. Вместо истинного значения x₀ (которое редко известно) используют среднее арифметическое

.

Среднее арифметическое – сумма вариант, деленная на число вариант. Варианта – численное значение единичного определения.

Единичное отклонение (случайное отклонение):

.

Выборочный метод состоит в вычислении характеристик совокупности на основе наблюдения части ее элементов на основе случайного отбора. Малая выборка – выборка небольшого объема, менее 20÷30 единиц.

Стандартное (выборочное) отклонение малой выборки отдельного определения:

S= ,

отклонение среднего результата:

.

Квадрат отклонения называют дисперсией.

S² – выборочная дисперсия отдельного определения;

– выборочная дисперсия среднего значения, служащая для оценки воспроизводимости.

Для малых выборок для определения границ доверительного интервала используют t-распределение Стьюдента

,

где t_p,f – коэффициент Стьюдента (коэффициент нормированного отклонения) для данной доверительной вероятности P и вариантности f=n-1.

Истинное значение x₀ или генеральное среднее находится в пределах, которые называются доверительные границы.

Дата добавления: 2017-01-14