Определение траектории, скорости и ускорения точки, при движении её в координатной форме

Решение

Определение положения центра тяжести плоского тела

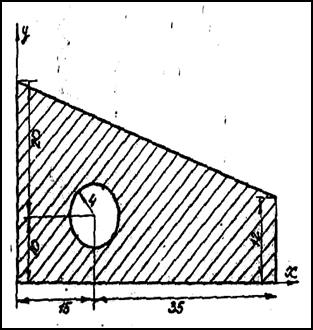
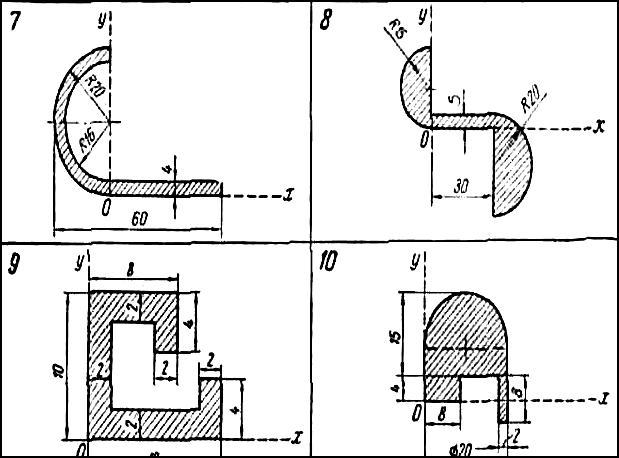
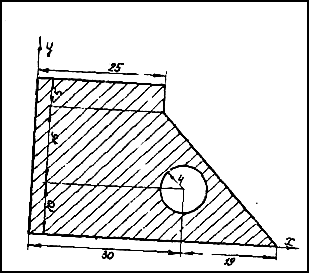
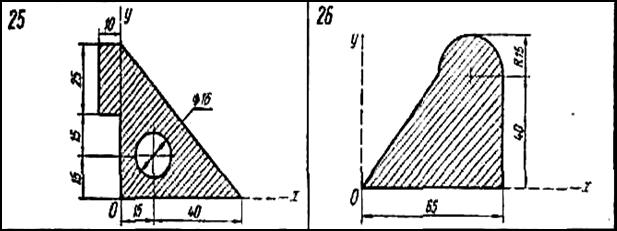
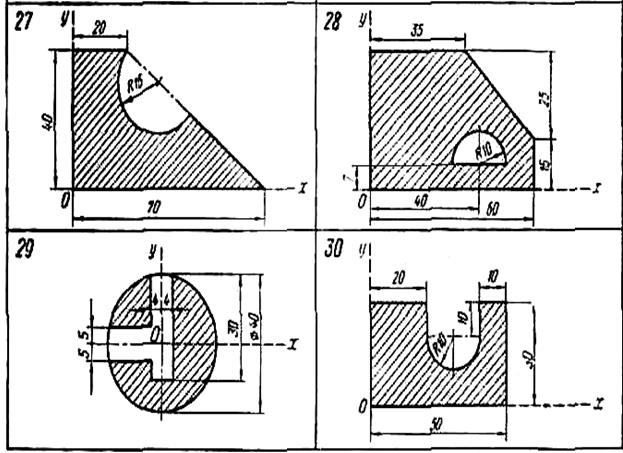
Найти координаты центра тяжести плоской фигуры, размеры — в сантиметрах.

Пример выполнения задания:

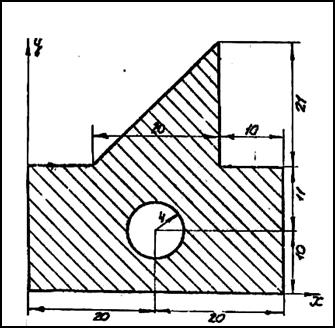
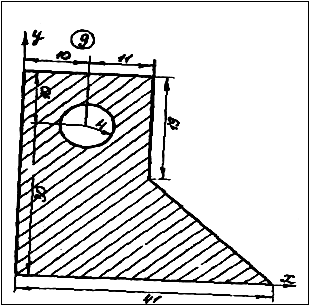
Определить координаты центра тяжести плоской фигуры, показанной на рис. 1.

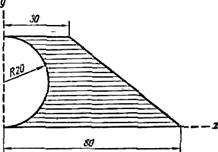
Рис.1

Координаты центра тяжести площади определяем по формулам:

x_C = 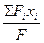; y _C = 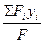. (1)

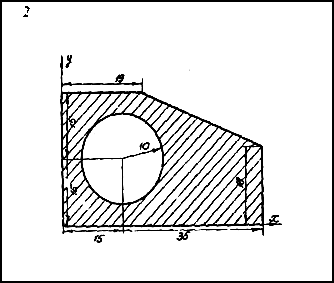
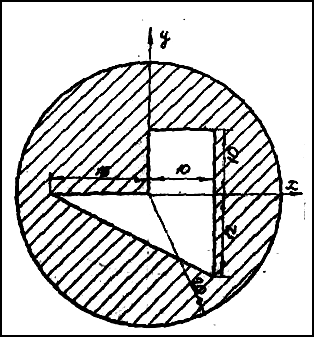
Чтобы воспользоваться этими формулами, площадь фигуры делим на отдельные части, положения центров тяжести которых известны. В данном случае такими частями являются: прямоугольник, треугольник и половина круга (рис.2). Площадь половины круга, вырезанную из площади прямоугольника, считаем отрицательной.

Имеем:

площадь прямоугольника

F ₁ = 40 • 30 = 1200 см²,

площадь треугольника

F ₂ = 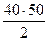= 1000 см²;

площадь половины круга

F ₃ = 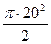= 200 p = 628 см ²

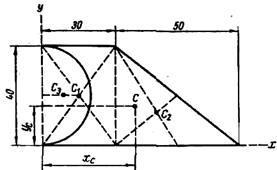
Рис.2

Центры тяжести рассматриваемых частей сечения имеют следующие координаты:

для прямоугольника

х ₁ = 15 см; у ₁ = 20 см;

для треугольника

x ₂ = 30 + 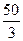= 46,7 см; y ₂ = 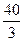= 13,3 см;

для половины круга

х ₃ = 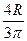= = 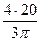8,5 см; y ₃ = 20 см.

Для вычисления координат центра тяжести плоской фигуры составляем таблицу.

Номер элемента	Fi,см ^2	xi,см	yi,см	Siy = Fi xi, см ^3	Six = Fi yi, см ^3
	-628	15,0 46,7 8,5	20,0 13,3 20,0	-5338	-12560
S		--	--

По формулам (1) вычисляем координаты центра тяжести плоской фигуры:

x _C = 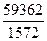=37,8 см; y _C = 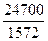=15,7 см.

Центр тяжести площади указан на рис. 2.

Если точка движется относительно некоторой системы координат, то координаты точки изменяются с течением времени. Уравнения, выражающие функциональные зависимости координат движущейся точки от времени, называют уравнениями движения точки в системе координат.

Движение точки в пространстве задается тремя уравнениями:

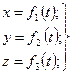(3.1)

Движение точки в плоскости (рис. 17) задается двумя уравнениями:

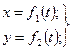(3.2)

Системы уравнений (1) или (2) называют законом движения точки в координатной форме.

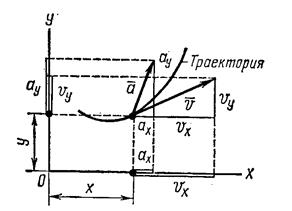
рис.17

Ниже рассматривается движение точки в плоскости, поэтому используется только система (2).

Если закон движения точки задан в координатной форме, то

A). траектория плоского движения точки выражается уравнением

,

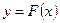которое образуется из данных уравнений движения после исключения времени ;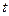

B).числовое значение скорости точки находится из формулы

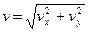
после предварительного определения проекции (см. рис. 17) скорости на оси координат

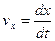и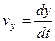

C).числовое значение ускорения находится из формулы

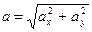
после предварительного определения проекций ускорения на оси координат

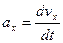и ;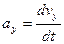

Направления скорости и ускорения относительно осей координат определяются из тригонометрических соотношений между векторами скорости или ускорения и их проекциями.

Используя уравнения движения точки в координатной форме, можно определить радиус кривизны траектории движущейся точки без непосредственного исследования уравнения траектории. Этот способ основан на том, что радиус кривизны траектории движущейся точки входит в формулу

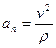
выражающую числовое значение нормального ускорения.

Отсюд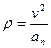а

. (а)

Скорость 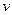точки определяется по формуле

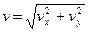. (б)

Следовательно,

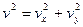. (б’)

Числовое значение нормального ускорения 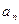входит в выражение полного ускорения точки

,

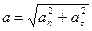откуда

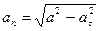, (в)

где квадрат полного ускорения

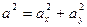(г)

и касательное ускорение

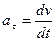. (д)

Расчетно-графическое задание №3.

Дата добавления: 2017-01-14