Расчетно-графическая работа 5

РАСЧЕТ СТАТИЧЕСКИ НЕОПРЕДЕЛИМЫХ РАМ МЕТОДОМ ПЕРЕМЕЩЕНИЙ

Методические указания

Нужно твердо усвоить идею метода перемещений, смысл основной системы и правила определения степени угловой и линейной подвижности рамы (степени кинематической неопределимости).

Для определения степени кинематической неопределимости удобно пользоваться следующей формулой:

n=n_у+n_л,

где n_у - число неизвестных углов поворота, равное числу жестких узлов рамы;

n_л - число неизвестных линейных перемещений, равное степени свободы шарнирной схемы рамы и определяемое по формуле n_л=Ш-3К, где Ш - число простых и приведённых к ним сложных шарниров, К - число замкнутых контуров рамы.

При выборе основной системы метода перемещений необходимо учитывать, что линейные связи должны быть поставлены не только по направлению возможных линейных перемещений, но и для устранения мгновенной изменяемости системы, образованной после постановки шарниров во все узлы (включая опорные).

Построение единичных и грузовых эпюр в основной системе производится по специальным таблицам. При этом значения ординат необходимо выражать через общую жесткость - EI.

9. Производим статическую проверку полученной эпюры. (рис.31)

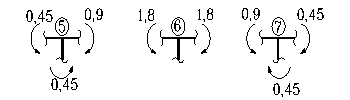
Рис.31

10. Деформационная проверка. Определяем вертикальное перемещение узла 6 в заданной системе. Для этого перемножим окончательную эпюру М на единичную эпюру в основной системе метода сил. (рис.32)

Рис.32

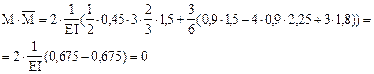
11. По эпюре моментов строим эпюру поперечных сил (рис.33):

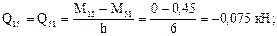
M₆₇= - 0,3 -1,5= -1,8 кНм;

M₇₆= - 0,6 -1,5= -0,9 кНм;

M₇₈= - 0,45= кНм;

M₈₇= 0.

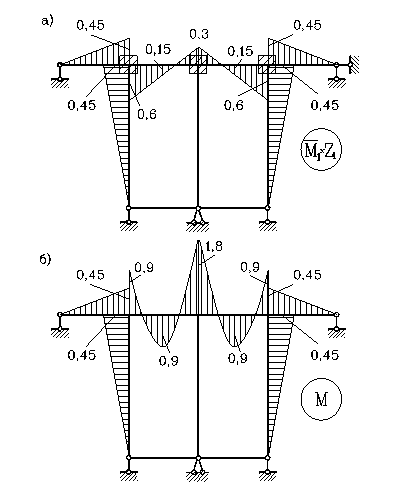
Рис.30

При определении коэффициентов следует внимательно следить за их знаками (r_ii>0), а также использовать теорему о взаимности реакций (r_ik=r_ki).

После определения значений неизвестных рекомендуется построить эпюры моментов по формуле

.

Суммирование этих эпюр рекомендуется производить по характерным точкам и в пояснениях обязательно проводить все расчеты.

Эпюры поперечных и продольных сил строятся по эпюре моментов так же, как и в контрольной работе 5.

Для проверки правильности эпюры M, необходимо составить условия статического равновесия узлов рамы по изгибающим моментам (статическая проверка).

ЗАДАЧА 1

Для заданной рамы (рис19.,а) требуется:

· построить эпюры изгибающих моментов, поперечных и продольных сил;

· проверить правильность построения эпюр.

Р е ш е н и е

1. Определяем степень кинематической неопределимости заданной рамы:

n_у = 1; n_л = 10-3×3=1; n =1+1=2.

Образуем основную систему, введя связи, препятствующие неизвестным угловому (подвижная заделка) и линейному (опорный стержень) перемещениям (рис.19,б).

Рис.19

3. Составим систему канонических уравнений метода перемещений для заданной рамы:

ì r₁₁Z₁+r₁₂Z₂+R_1p=0;

í

î r₂₁Z₁+r₂₂Z₂+R_2p=0.

4. Используя таблицу 1 приложений, построим для основной системы единичные (рис.20,а,б). и грузовую эпюры (рис.20,в).

5. Применяя метод вырезания узлов, определим коэффициент при неизвестном и свободный член канонического уравнения (рис.29).

Рис.29

Из рис.29 имеем:

R_1P= - (1,5+1,5)= - 3 кНм

6. Подставляем найденные значения в уравнение и решаем его:

6,67EI×Z₁ - 3=0; Z₁=0,45/EI;

7. Строим исправленную эпюру (рис.30,а).

8. Строим окончательную эпюру изгибающих моментов (рис.30,б):

M₁₂= M₂₁= M₂₃= M₃₂=0

M₂₆= M₆₂=0;

M₁₅= 0;

M₅₁= 0,45кНм;

M₃₇= 0;

M₇₃= 0,45кНм;

M₄₅= 0;

M₅₄= 0,45кНм;

M₅₆= - 0,6 -1,5= -0,9 кНм;

M₆₅= - 0,3 -1,5= -1,8 кНм;

3. Так как внешняя нагрузка симметричная, то обратносимметричные неизвестные заведомо равны нулю: Z₂= Z₃= Z₄=0. Каноническое уравнение метода перемещений будет иметь следующий вид:

r₁₁Z₁ +R_1p=0;

4. Используя таблицу 2 приложений, построим для основной системы единичную (рис.28,а). и грузовую эпюры (рис.28,б).

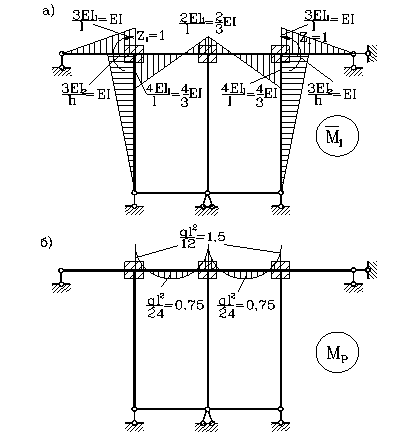
Рис.28

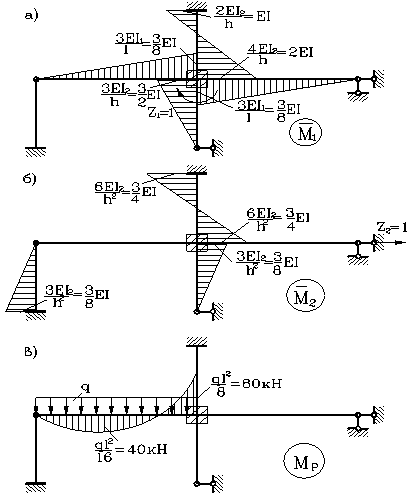
Рис.20

5. Определяем коэффициенты при неизвестных и свободные члены системы канонических уравнений. Для этого вырежем вначале узел 5 и рассмотрим условие его равновесия

6. (åМ=0), т.е. определим коэффициенты и свободный член первого уравнения, представляющие собой реактивные моменты во введённой заделке (рис.21,а,б,в).

Рис.21

Из рис.21,а,б,в имеем:

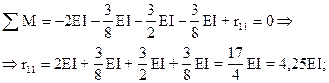
Для определения коэффициентов второго уравнения, представляющих реакции во введённом стержне, рассечём стойки и рассмотрим условие равновесия (åX=0) средней части рамы, содержащей введённый стержень (рис.22,а,б,в).

Из рис.22,а,б,в следует:

ЗАДАЧА 2

Для заданной рамы (рис27.,а) требуется:

· построить эпюры изгибающих моментов, поперечных и продольных сил;

· проверить правильность построения эпюр.

Р е ш е н и е

1. Определяем степень кинематической неопределимости заданной рамы:

n_у=3; n_л=19-3×6=1; n=3+1=4.

2. Образуем основную систему метода перемещений, применяя группировку неизвестных (рис.27,б).

Рис.27

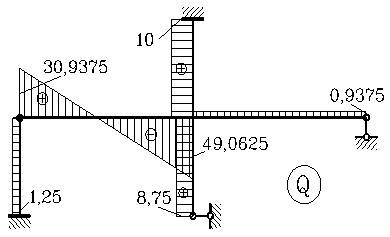
Рис.25

11. Методом вырезания узлов строим эпюру продольных сил (рис.26).

Рис.26

Рис.22

6. Подставляем найденные значения в систему уравнений и решаем её:

ì 4,25EI×Z₁+0,375EI×Z₂+80=0;

í

î 0,375EI×Z₁+0,5625EI×Z₂=0.

Z₁=-20/EI; Z₂=13,333/EI.

7. Строим исправленные эпюры, умножая каждую единичную эпюру на соответствующее найденное перемещение (рис.23,а,б). При этом знак у первой эпюры изменится на противоположный, т.к. Z₁ имеет отрицательное значение.

8. Строим окончательную эпюру изгибающих моментов, суммируя исправленные и грузовую эпюры (рис.24,а):

Рис.23

M₁₄=5 кНм;

M₄₁=0;

M₅₄=7,5-80=-72,5 кНм;

M₄₅=0;

M₅₆=-40+10=-30 кНм;

M₆₅=20-10=10 кНм;

M₅₂=-30-5=-35 кНм;

M₂₅=0;

M₅₃=-7,5= кНм;

M₃₅=0.

Рис.24

9. Производим проверку полученной эпюры. Для этого вырежем узел 5 (рис.24,б) и проверим условие равновесия вида: åM=0;

åM=-72,5+30+7,5+35=0 - условие выполняется.

10. По эпюре моментов строим эпюру поперечных сил (рис.25):

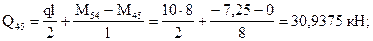
МИНИСТЕРСТВО СЕЛЬСКОГО ХОЗЯЙСТВА РФ

Департамент научно-технологической политики и образования

ФГОУ ВПО Костромская ГСХА

Кафедра сопротивления материалов и графики

МЕТОДИЧЕСКИЕ УКАЗАНИЯ

к расчётно-графическим работам по курсу

«Строительная механика»

(часть 2)

Кострома 2011

УДК 624.04

Методическое пособие составил: Афанасьев Е.Н.

Рекомендовано Методической комиссией архитектурно-строительного факультета КГСХА

Рецензент: доцент, к.т.н. Гуревич Т.М.

В методическом пособии даются в конспективной форме рекомендации о методах расчета задач, приводятся необходимые формулы, таблицы и примеры решения задач.

Дата добавления: 2017-01-14