Формування альтернативних варіантів рішень і багатокритеріальний вибір

Багатокритеріальний вибір при обґрунтуванні інженерних рішень

ЛЕКЦІЯ 12

План

1. Формування альтернативних варіантів рішень і багатокритеріальний вибір.

2. Багатокритеріальний вибір за відстанню до цілі.

3. Багатокритеріальний вибір за методом послідовного застосування критеріїв.

Системний підхід часто викликає необхідність формування множини альтернативних варіантів рішення і застосування декількох критеріїв для оцінки і вибору кращого варіанту. Це обумовлено тим, що дерево цілей на нижньому рівні може мати низку цілей, що не зводяться до однієї (наприклад, підвищити продуктивність і показник екологічності робіт). Крім того, кожна ціль може бути досягнута різними засобами.

Багатокритеріальність проявляється особливо чітко при розробці та реалізації дорогих проектів (інженерно-технічний комплекс, технологіч­ні комплекси, станція ТО та ін.). У таких випадках потрібно враховувати не менше чотирьох узагальнених критеріїв, а саме: корисність (функціо­нальні критерії), сукупна вартість (економічні критерії), строк реалізації та освоєння (часові критерії), екологічність і техніка безпеки (наслідки).

Проблема полягає в тому, що кожен із узагальнених критеріїв досягає свого кращого значення при різних поєднаннях характеристик системи. Можлива також наявність суперечливих критеріїв, коли зміна характе­ристик системи з метою покращення одного з них викликає погіршення іншого. Побудова єдиної шкали для оцінки всієї сукупності критеріїв, що мають різний фізичний зміст, викликає значні труднощі.

У загальному вигляді математична модель (ММ) багатокритеріальної задачі описується виразом:

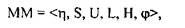(12.1)

де η — тип багатокритеріальної задачі (оптимізація, ранжування, вибір);

S — множина варіантів характеристик системи, що оцінюється;

U — множина критеріїв, за якими оцінюється система;

L — шкала оцінок по кожному критерію;

H — система пріоритетів ОПР на множині варіантів S;

φ — правило вирішення, яке на множині варіантів S задає відношен­ня переваги відповідно до системи пріоритетів Н.

Для пошуку кращого рішення необхідно множину варіантів S пред­ставити у просторі критеріїв U зі шкалами оцінок L і відповідно до пра­вила вирішення φ впорядкувати цю множину, використовуючи систему пріоритетів Н. Найскладнішим етапом побудови моделі є встановлення правила вирішення φ.

У методах розв’язку багатокритеріальних задач можна виділити два напрямки: оптимізація і вибір, які відрізняються насамперед правилом вирішення.

Оптимізаційні методи застосовують у тих випадках, коли вдається окремі критерії звести до одного узагальненого (інтегрального). В цьому випадку правилом вирішення будуть детерміновані методи оптимізації функцій з багатьма змінними. Інтегральний критерій може бути ади­тивним, мультиплікативним або мультиадитивним (комбінованим). Основні труднощі цієї групи методів пов’язані з побудовою пред­ставницького інтегрального критерію, визначенням вагових коефіцієнтів окремих критеріїв, що входять в узагальнений, забезпеченням чутливості багатофакторної моделі, великою розмірністю моделей та ін. Тому методи багатомірної оптимізації доцільно застосовувати для вирішення разових задач перспективного планування.

У повсякденній інженерній діяльності частіше застосовують мето­ди багатокритеріального вибору рішення із множини можливих варіан­тів. При цьому істотно зростає роль ОПР і його системи цінностей. Вона проявляється, перш за все, на стадіях формування вихідної множини альтернативних варіантів (ВМА), вибору критеріїв і міри їх значущості, багатокритеріальної оцінки і прийняття рішення. Ефективність рішень безпосередньо залежить від професійного рівня ОПР, його вміння засто­совувати сучасні методи і прийоми аналізу та синтезу рішень за декілько­ма критеріями.

Для полегшення процедури вибору рішення важливо гранично змен­шити число альтернативних варіантів. При формуванні ВМА широко за­стосовується метод Парето, який дозволяє виділити ефективні варіанти з урахуванням всіх критеріїв. Для знаходження ефективних (Парето-оптимальних) варіантів застосовують принцип домінування.

Нехай варіанти, що порівнюються, оцінюються вектором критеріїв:

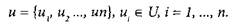
Тоді варіант А домінує над варіантом В (А>|В), якщо кожен з критеріїв иА_і переважає або еквівалентний до відповідних критеріїв иВ_і, причому хоча б для одного з них справедлива строга перевага (и^А > и^в). Знак пере­ваги (>) відображає систему Н пріоритетів ОПР. Якщо критерій и_і вира­жений кількісно і покращення варіанту відповідає його збільшенню, то знак переваги відповідає знаку «більше» (и^А > и^в). Якщо покращення ва­ріанту відповідає зменшенню кількісно вираженого критерію и_i, — знаку менше (и^A < и^в). Крім того, від може застосовуватись і до критеріїв, що не мають кількісного виразу, але входять до системи цінностей ОПР (ес­тетичні характеристики, техніка безпеки тощо). Отже, знак переваги (>) є універсальним щодо оцінки властивостей об’єкта.

Суть сказаного розглянемо на конкретному прикладі з двома критері­ями, який дозволяє привести графічне зображення варіантів на площині.

Приклад: Із множини можливих агрегатів для внесення мінеральних добрив потрібно виділити Парето-оптимальні варіанти за критеріями продуктивності ( W ) і паливної економічності (G). Бажано, щоб пошук кращих варіантів зводився до максимізації (або мінімізації) обох критеріїв. Тому для оцінки палив­ної економічності приймемо величину, що обернена до погектарної витрати палива G. Тобто це буде площа, яку обробить МТА, витративши 1 л палива. Вихідні дані для прямоточної схеми внесення добрив наведені в таблиці 12.1, а реалізація варіантів в просторі критеріїв W і F_q— на рис. 12.1.

Таблиця 12.1. Вихідні дані для порівняння МТА

Варіант	Склад МТА	Wj, га/год	Fqj, га/кг
	Т-150К + МВУ-8Б	7,0	0,31
	МТЗ-80 + 1РМГ-4	5,1	0,71
	МТЗ-80 + СТТ-10	6,5	0,71
	МТЗ-80 + СП-11 + 2РТТ-4,2	4,1	0,67
	МТЗ-80 + МВУ-0,5	4,9	0,55
	ЮМЗ-6Л + 1РМГ-4	4,0	0,55
	ЮМЗ-6Л + СП-11 + 2РТТ-4,2	3,9	0,91
	ЮМЗ-6Л + МВУ-0,5	4,5	0,53
	Т-40М + МВУ-0,5	4,1	1,00
	Т-40М + РТТ-4,2	2,6	0,59
	Т-25А + МВУ-0,5	2,4	1,35
	Т-25А + РТТ-4,2		1,00

Відповідно до принципу домінування виділимо кращі варіанти, прийнявши за початковий варіант S₁₀.

Рис. 12.1. Приклад побудови ефективної границі (множини Парето) при двох критеріях за даними таблиці 12.1.

Тоді варіант S ₄ домінує над S ₁₀ ( S ₄ >|S₁₀) бо W ₄ > W ₁₀ і F_q4 > F_q10; варіант S ₂ домінує над S ₄ ( S ₂ >|S₄) бо W ₂> W ₄ і F_{q 2} > F_{q 4} варіант S₃ домінує над S ₂ (S₃ >| S ₂), бо W ₃ > W ₂ при F_{q 3} = F_{q 2}.

Отже, ряд домінування має вигляд S₃>| S ₂ >| S ₄ >| S₁₀. У множині варіантів можуть бути і такі, що не домінують над іншими, але й над ними немає домінуючого варіанту. Для нашого прикладу таким буде варіант бо хоча він і є найпродуктивнішим, але поступається всім іншим за паливною економічністю.

Метод аналізу Парето дозволяє вийти на ефективну границю, яка об’єднує варіанти, що домінують над іншими і не мають домінування над собою. Варіанти, що лежать на ефективній границі, називаються Парето-оптимальними. Для наведеного прикладу на ефективній границі лежать варіанти S₁ S₃, S₉ і S ₁₁. Зменшити число варіантів ВМА можна введенням обмежень на гранично допустимі значення критеріїв. Так, обмеживши мінімальне значення продуктивності W_mіn=4 га/год і виробітку на одиницю витраченого палива F_qmin =0,6 га/кг, ОПР може звести задачу до вибору одного з варіантів (S₃ і S₉).

Метод Парето може застосовуватись і для більшого числа критеріїв, особливо при застосуванні комп’ютерів.

Дата добавления: 2015-07-13