Графоаналітичні моделі і номограми у прийнятті рішень

ЛЕКЦІЯ 8

Детерміновані моделі прийняття інженерних рішень

План.

1. Графоаналітичні моделі і номограми у прийнятті рішень.

2. Побудова логарифмічних номограм із сорокап’ятиградусним ходом.

Номограма — це графічне зображення функціональних зв’язків між фізичними величинами. Їх перевагами є наочність, простота у викорис­танні, можливість вирішення обернених задач, в яких при зафіксованому значенні залежної змінної (функції) знаходяться відповідні значення незалежних змінних (факторів). При цьому забезпечується достатня для інженерних розрахунків точність, яка залежить від обраних масштабів і якості побудови номограм.

Будь-яке рівняння з двома змінними типу у = f(х) можна зобразити у вигляді графіка на площині в прямокутній системі координат (рис. 8.1, а). При цьому шкали можуть бути як рівномірними, так і нерівномірними (логарифмічними, квадратичними, оберненими і т.п.). Довжина шкали за­лежить від граничних значень змінної і прийнятого масштабу.

Масштаб шкали визначається довжиною відрізку, що відповідає оди­ниці виміру даної змінної і називається модулем шкали. Тоді рівняння прямолінійної рівномірної шкали та її модуль можуть бути записані так:

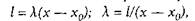
де λ — модуль шкали, який вимірюється переважно в міліметрах;

х₀ і х — відповідно початкове та поточне значення змінної, для яко­го визначають положення позначки на шкалі;

l — відстань від початкової до поточної позначки на шкалі. Якщо значення х є кінцевим, то l характеризує довжину шкали.

Рис. 8.1. Номограми функцій:

а) однієї змінної; 1-у=1,5х; 2 —у = 0,5х²;

б) двох змінних y = х²z;

в) двох змінних типу у = ахz

Приклад: Для шкали довжиною l = 100 мм при 0 <х< 10

λ = l/х = 100/10 = 10 мм, а при 20 < х < 45

λ = l/(х — х0) = 100/ (45 — 20) = 4 мм.

Рівняння логарифмічної шкали має вигляд l = λ lgх. Оскільки lg1 = 0, а lg10=1, то l₁ = λlg1 = 0 і l₁₀ = λlg10=λ.

Тому на початку логарифмічної шкали ставлять 1, а на відстані λ позначку 10. Отже, довжина логарифмічної шкали від 1 до 10 дорівнює модулю.

Графічна побудова рівнянь з трьома змінними типу z= f (х, у) може бути зведена до побудови серії графіків рівнянь з двома змінними при зафіксованому значенні третьої змінної, яка стає параметром функції (рис. 8.1, б). Переважно параметром роблять ту змінну, яка приймає лише декілька дискретних значень або змінюється в менших порівняно з іншими межах.

Якщо при побудові рівнянь з трьома змінними графіки мають вигляд пучка прямих зі спільним початком або сім’ї паралельних прямих, то до­цільно побудувати шкалу і для третьої змінної (рис. 8.1, в). Це спрощує по­будову прямої для будь-якого проміжного значення третьої змінної (па­раметру). Шкала параметру залежить від показника степеня при змінній. У наведеному рис. 8.1 в показник степеня при змінній у дорівнює 1, тому шкала у є рівномірною. Якщо показник степеня при цій змінній дорівню­вав би 2, то шкала була б квадратичною і т. д. Загальним прийомом побудови третьої шкали є побудова сім’ї прямих при зафіксованому значенні параметру, продовження цих прямих до перетину із шкалою параметру, проставляння відповідних числових значень на шкалі з наступним нане­сенням поділок між відомими значеннями змінної.

Для тих рівнянь з трьома змінними, які можуть бути подані у вигляді z=f(х)·f(y), зручно будувати номограму в двох спряжених квадрантах (рис. 8.2). У цьому випадку рівняння розбивають на два з введенням до­даткової змінної t:

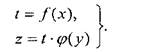(8.1)

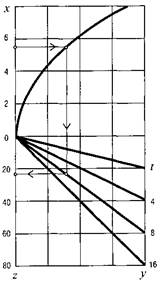
Рис. 8.2 Номограма .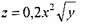

Обидва рівняння мають спільну шка­лу t. Далі побудова проводиться за описа­ними вище правилами.

Приклад: Нехай потрібно побудувати номограму рівняння:

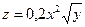для 0 ≤x≤ 10 і 0 ≤y≤ 25.

Виділимо два рівняння введенням допоміжної змінної t:

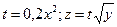
Номограма даних рівнянь наведена на рис. 8.2. Звернемо увагу на те, що шкала у є шкалою квадратних коренів.

Аналогічно будуються номограми для кількості змінних більше трьох, якщо рів­няння можна записати у вигляді добутку функціональних залежностей окремих змінних, тобто:

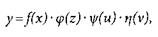(8.2)

де х, z, и, v — незалежні змінні.

Такі номограми будуються у спряже­них квадрантах із введенням допоміжних змінних, наприклад t, s і р у рів­няннях:

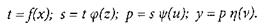
Побудова номограми системи рівнянь (8.2) може бути здійснена в чо­тирьох спряжених квадрантах (рис. 8.3).

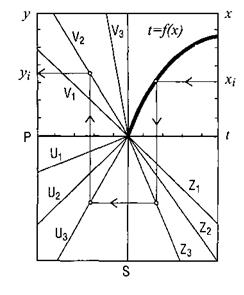
Рис. 8.3. Схема номограми у чоти­рьох спряжених квадрантах

Дата добавления: 2015-07-13