Расчет зубьев на контактную прочность

Силы, действующие в зацеплении

При работе зубчатой передачи между зубьями сопряженных колёс возникают силы нормального давления F_n, направленные по линии зацепления. Вместе с тем, в результате относительного скольжения профилей зубьев в зацеплении возникаю­т силы трения F_f = f∙F_n (f – коэффициент трения).

При определении усилий в зацеплении силами трения пренебрега­ют, поскольку величина коэффициента трения в зоне контакта мала. При наличии смазки в зацеплении f = 0,05...0,08 [2, c. I85].

Силу нормального давления на зуб колеса F_n можно разложить на две составляющие:

· окружную F_t, направленную по касательной к окружности, и

· радиальную F_r, направленную по радиусу колеса к его центру.

Окружную и радиальную составляющие силы F_n можно определить по зависимостям:

F_t = F_n ∙ cos α_tw; F_r = F_n ∙ sin α_tw(5.9)

С другой стороны, составляющие силы нормального давления могут быть определены следующим образом:

F_t = T / (0,5 d_tw); F_r = F_t ∙ tg α_w. (5.10)

На работоспособность передачи оказывают влияние контактные напряжения σ _H, возникающие в поверхностном слое рабочей гра­ни зуба (рис. 5.2), и напряжения изгиба σ _F, действующие в по­перечном сечении ножки зуба, т.е. в сечении у его основания (рис. 5.3).

Расчет на усталостную прочность зубьев эвольвентных закрытых передач стальными колесами с модулем не менее 1,00 мм стандартизо­ван ГОСТ 21354-87, который регламентирует структуру расчетных за­висимостей.

При расчете зубьев на контактную прочность принят индекс “H” (по имени автора теории расчета Herz – Герца). При расчете зубьев на усталостную прочность по напряжениям изгиба – индекс “F” (от анг­лийского слова “foot” – нога).

Согласно ГОСТ 21354-87:

а) общие коэффициенты для расчета по контактным напряжениям σ _H и напряжениям изгиба σ _F, обозначены буквой “К”;

б) специфические коэффициенты только для расчета по контактным напряжениям σ _H обозначены буквой “Z”;

в) специфические коэффициенты для расчета по напряжениям изгиба σ _F обозначены буквой “Y”.

Расчет выполняют для зацепления в полюсе, т.к. выкраши­вание рабочих поверхностей зубьев начинается у полюсной линии.

В качестве исходной принята формула Герца для определения максимальных контактных напряжений σ _{H max} (см. рис. 5.2), возникающих при сжатии двух цилиндров, соприкасающихся по образующим.

Таким образом, задача контакта двух зубьев эвольвентного профиля сводится к задаче контакта двух цилиндров радиусами ρ₁ и ρ₂:

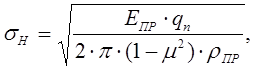(5.11)

где Е_пр – приведенный модуль Юнга материалов парных колес;

Е_пр = 2Е₁ ∙Е₂ /(Е₁ +Е₂);

q_n – удельная нормальная нагрузка на зуб, т.е. нагрузка, действующая на единицу длины зуба (см. рис. 5.3);

ρ_пр – приведенный радиус кривизны профилей зубьев, зацепляющихся в полюсе п (см. рис. 5.2);

(5.12)

В ф. (5.12) знак “+” принимают для внешнего зацепления колес, а знак “– “ используют для внутреннего зацепления.

Рис. 5.2. – К расчету эвольвентного зацепления

на контактную прочность зубьев

Расчетная удельная нормальная нагрузка на зуб, выраженная через окружную силу в зацеплении F_t, может бытьопределена по зависимости:

(5.13)

где K_Hα – коэффициент, учитывающий неравномерность распределе­ния на грузки между зубьями; для прямозубых колес K_Hα = 1,0;

K_Hβ – коэффициент неравномерности распределения нагрузки по длине контактных линий зубьев; выбирают по соответствующим таблицам в за­висимости от твердости зубьев и ширины колеса [3, c.I39];

K_HV – коэффициент динамической нагрузки, возникающей в за­цеплении [3, c. 138];

b_w – рабочая ширина зубчатого венца колеса (или длина зуба);

b_w =ψ_вa ∙ a_w .

Из рис. 5.2 видно, что: ρ₁=0,5d_w1 ∙sin d_w; ρ₂=0,5d_w2 ∙sin d_w (5.14)

Вместе с тем, начальные диаметры колеса и шестерни связаны между собой зависимостью d_w2 = d_w1 ∙u.

Тогда, учитывая (5.12) и (5.14), получим:

(5.15)

Подставив значения q_n и ρ_пр в (5.11) и выполнив некоторые преобразования, получим:

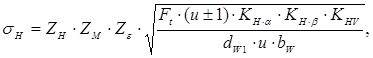(5.16)

где Z_н – коэффициенты формы сопряженных поверхностей зубьев в полюсе зацепления; . При α_w=20⁰ Z_H=2,5;

Z_Е – коэффициент, учитывающий механические свойства материалов сопряженных колес; 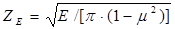; для стальных колес Z_Е = 190 Н ^1/2 /мм;

Z_ε – коэффициент, учитывающий суммарную длину контактных линий сопряженных зубьев; 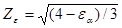; для прямозубых колёс (при ε_σ = 1,6) коэффициент Z_ε = 0,9.

Если подставить в формулу (5.16):

b_w =ψ_ва ∙а_w, F_t = T₂ / (0,5 d_w2) d_w2 = d_w1 ∙u=2a_w ∙u / (u± 1), то получим условие обеспечения контактной прочности зубьев колёс:

(5.17)

где Т₂ – в Н∙мм; σ_н, σ_нР2 – в МП а; а_w – в мм.

Современные технологии изготовления зубчатых передач требуют, чтобы запас прочности по контактным напряжениям не превышал 15%,а перегрузка – не более 5% [3, с.159]. Если результаты проверочного расчета передачи по контактным напряжениям подтвердят эти ограничения, то параметры передачи считают окончательными. Иначе – необходим перерасчет геометрических параметров передачи.

Если перегрузка зубьев превысит 5%, то можно принять меры:

· увеличить ширину зубчатого венца: перейти к следующему стандартному значению коэффициента ширины ψ _ba;

· увеличить межосевое расстояние: перейти к следующему стандартному значению, включая и второй ряд значений а_w;

· назначить другие, более прочные материалы и термообработку для изготовления шестерни и колеса.

Меры перечислены в порядке их усиления.

Из (5.17) может быть получена зависимость для проектного расчета цилиндрической прямозубой передачи:

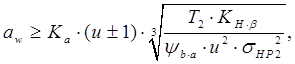(5.18)

где К_а – коэффициент межосевого расстояния; для прямозубых передач

К_а = 49,5(Н/мм²)³; для косозубых и шевронных передач: К_а = 43(Н/мм²)³; расчетная формула: .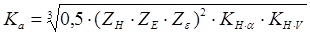

Рассчитанное по (5.18) межосевое расстояние должно быть сог­ласовано со стандартным значением по ГОСТ 2185-66.

Входящее в формулы (5.17) и (5.18) параметр σ_нР2 – допускаемые контактные напряжения материала того из зацепляющихся зубчатых колес, для которого принят материал меньшей прочности. Как правило, менее прочными выполняют зубья колеса, т.к. они реже попадают в зацепление, чем зубья шестерни. Величину допускаемых контактных напряжений определяют по зависимости:

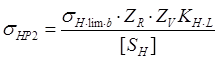(5.19)

где σ _{H lim в} –предел контактной усталости поверхностей зубьев, соответствующий базовому числу циклов напряжений; его рассчитывают по эмпирическим зависимостям в функции поверхностной твердости материалов колес [4, 185] или [2, с.193];

[S_H] – коэффициент безопасности; при однородной структуре материал колеса [S_H]=1, при поверхностном уп­рочнении зубьев колес [S_H] =1,2 [4 с. 185];

Z_R – коэффициент, учитывающий шероховатость сопряженных поверхностей зубьев; при R_a= 1,25…0,63 мкм Z_R=1,0;

при R_a = 2,50…1,25 мкм Z_R = 0,95; при R_a = 10,5…2,5 мкм Z_R =0,9[4,c.185];

Z_V – коэффициент, учитывающий влияние скорости в зацеплении; при НВ≤350: Z_V = 0,85∙v^0,1; при НВ >350: Z_V = 0,929∙v^0,03; в расчетах нормальной точности принимают: Z_V = 1,00…1,15 [4.c.185];

K_Hl –коэффициент долговечности; 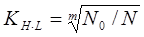; (базовое число циклов N_o=10⁶ и N – фактическое число циклов нагружения зубьев колес за весь срок службы передачи); при постоянной нагрузке K_Hl= 1,0.

Дата добавления: 2015-07-13