Расчет зубьев на изгиб

При расчете зубьев на изгиб принимают два допущения:

1. Зуб рассматривают как балку, жестко защемленную одним
концом и нагруженную силой F_n, приложенной к вершине зуба
(рис. 5.3). Такое положение нагрузки является наихудшим для зуба, т.к. плечо силы F_n относительно опасного сечения зуба имеет наибольшую величину. За опасное сечение зуба принимают сечение его основания в зоне наибольшей концентрации напряжений.

2) За расчетную силу принимают полную силу зацепления F_n,
следовательно, предполагают, что одновременно в зацеплении участвует только одна пара зубьев.

Перенесём силу F_n вдоль линии действия в точку, расположенную на оси симметрии зуба, и разложим на две составляющие:

· си­лу F_t', вызывающую в опасном сечении зуба напряжения изгиба σ _изг, и

· силу F₂', взывающую в зубе напряжения сжатия σ _сж.

Известно, что угол профиля зуба при вершине немного больше угла зацепления (α’ _w > α_w), поэтому и силы F_t'= F_n∙cos α’_w и

F_r'= F_n ∙sin α’_w несколько отличаются от сил, возникающих в зацеплении.

Этот расчетный случай пригоден для выполнения основных рас­четов передач общего назначения. Как видно из рис. 5.3,б, результирующие напряжения на растянутой стороне зуба (точка А) мень­ше, чем на сжатой. Вместе с тем, известно, что любой материал об­ладает большей прочностью на сжатие, чем на растяжение. Именно поэтому образование усталостных трещин начинается на растянутой стороне зуба, т.е. в точке А.

Вспомним, что для открытых передач основной вид разрушения – это поломка зубьев за счет действия напряжений изгиба, поэ­тому и основной показатель передачи, модуль “ т”, рассчитывают из условия усталостной прочности зубьев колёс по напряжениям изгиба. Затем передачу конструируют и проверяют по контактным напряжениям.

Для закрытых передач расчет зубьев на усталостную прочность по напряжениям изгиба σ _F является проверочным.

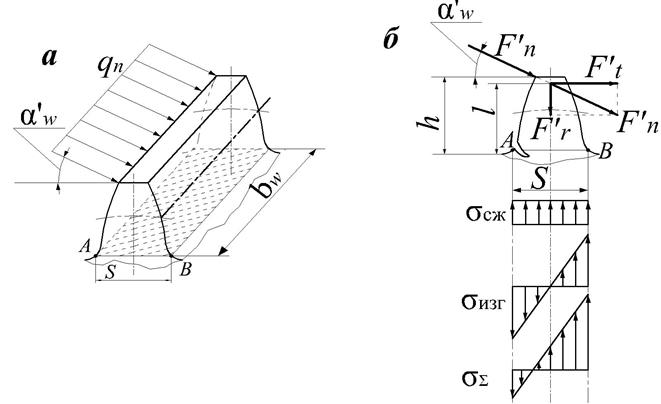
Рис. 5.3. – К расчету зубьев эвольвентных колес на усталостную прочность по напряжениям изгиба

Итак, наибольшее напряжение изгиба на растянутой стороне зуба, в точке А (см. рис. 5.3, б):

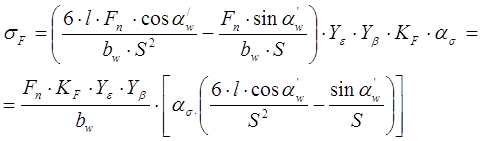(5.20)

где α_σ – теоретический коэффициент концентрации напряжений;

Υ_ε – коэффициент перекрытия зубьев; для передач общего назначения Υ_ε =1 [7, с. 193];

Υ_β – коэффициент угла наклона зубьев; для прямозубых ко­лес Υ_β =1,0 [4, c.171]

K_F – коэффициент нагрузки.

Коэффициент нагрузки при расчете зубьев на изгиб:

K_F =K_Fα ∙ K_Fβ ∙ K_Fv, (5.21)

где K_Fα – коэффициент распределения нагрузки между зубьями, выбирают в зависимости от скорости в зацеплении и степени точности передачи; для передач общего назначения K_Fα= 1,0 [7, c. 184];

K_{F β} – коэффициент неравномерности распределения нагрузки по длине зу­ба; для прямозубых прирабатывающихся колес: K_Fβ =1,0 [3,c.141]; для не прирабатывающихся колес этот ко­эффициент выбирают в зависимости от поверхностной твердости зубьев и расположения колес в передаче (например, по табл. 9.2 [3, c. 14l]);

K_Fv – коэффи­циент динамической нагрузки, выбирают в зависимос­ти от скорости в зацеплении и поверхностной твердос­ти зубьев. Например, при v≤ 5 м/с и твердости зубьев НB ≤ 350: коэффициент K_Fv =1,4 [3, c. 141].

Выполним некоторые преобразования зависимости (5.20):

1) умножим и разделим правую часть выражения на величину модуля т;

2) выразим силу F_n через силу F_t по ф. (5.9): .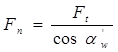

Зависимость (5.20) примет вид:

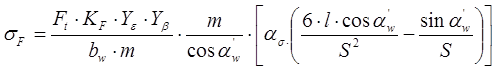(5.20, а)

Обозначим произведение выражения в квадратных скобках и (m/cosd_w) буквой Υ_F, тогда ф.(5.20, а) примет вид:

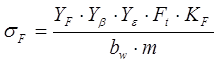(5.22)

где Υ_F – коэффициент формы зуба.

Величина коэффициента Υ_F зависит от числа зубьев колеса и смещения исходного контура [4, c.170].

С учетом (5.10) и (5.3) получим условие обеспечения усталостной прочности зубьев цилиндрических колес по напряжениям изгиба:

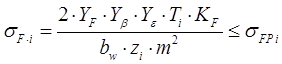(5.23)

где T_i – вращающий момент на шестерне (i=1) или колесе (i=2), Н∙мм;

σ_F, σ_FР –фактические и допускаемые напряжение изгиба, мПа.

Следует иметь в виду, что:

· проверочному расчету зубьев на усталостную прочность по напряжениям изгиба подвергают то колесо передачи, для которого соотношение 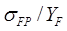меньше;

· материалы и термообработка для шестерни и колеса назначены правильно, если соотношения 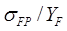примерно равны.

Если проверочный расчет показал перегрузку зубьев более 5%, то следует увеличить значение модуля (при этом изменятся числа зубьев шестерни и колеса) и расчет повторить. Поскольку межосевое расстояние при этом не меняют, то и контактная прочность зубьев сохранится на том же уровне.

Допускаемые напряжения изгиба материала колеса (или шестерни) определяют аналогично допускаемым контактным напряжениям (см. ф. (5.19)):

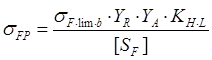(5.24)

где σ _{F lim в} – предел выносливости зубьев при изгибе, соответствующий базовому числу циклов напряжения N₀ = 4∙10⁶[4, c.187];

K_Fl – коэффициент долговечности, K_Fl =1,0 при N ≥N₀;

Υ_а – коэффициент, вводимый при двустороннем приложении нагрузки (при реверсировании), при одностороннем действии нагрузки на зуб Υ_а = 1,0 [4, c.188];

[S_F] – коэффициент запаса прочности по напряжениям изги­ба; выбирают в зависимости от технологии изготовления зубчатых колес и степени ответственнос­ти передач: [S_F] =1,4…2.2. Для передач обще­го назначения [S_F]=1,7 [4, с.186].

Современные технологии изготовления зубчатых передач требуют, чтобы запас прочности по напряжениям изгиба не превышал 15%, а перегрузка зубьев не превышала 5%.

Однако, для передач общего назначения это требование применительно к изгибной прочности зубьев, чаще всего, не выполняется. Ресурс прочности по напряжениям изгиба много больше, чем 15%. Добиться выполнения этих требований можно:

· путем уменьшения размеров опасного сечения ножки зуба (см. рис. 5.3) или

· понижения прочности материала колеса, но эти меры могут привести к перегрузке зубьев колёс по контактным напряже­ниям свыше 5%.

Вместе с тем, каждый зуб шестерни чаще (в передаточное число раз) попадает под нагрузку, поэтому для обеспечения примерно равной прочности зубьев шестерни и колеса шестерню выполняют из более прочного материала.

Если условие (5.22) не выполняется, т.е. запас прочности превышает 15%, то это допустимо, так как нагрузочная способность большинства закрытых зубчатых передач ограничивается контактной прочностью зубьев [3, с.144].

И поскольку основная причина разрушения зубьев закрытых передач – это усталостное поверхностное выкрашивание зубьев колёс (Питтинг–процесс), то запас прочности зубьев по напряжениям изгиба может быть и более 15%.

Дата добавления: 2015-07-13