Оно означает, что свободно могут быть выбраны только 1 или 2 угла наклона осей ОСК к ФКП

Пример:

y_x =45°, y_y=30° Þ Sin²(y_z)= 1-(0.4071)²-(0.5)²=0.25 Þ y_z=30°;

Сами:

y_x =45°, y_y=45° Þ Sin²(y_z)= 1-(0.5)²-(0.5)²=0Þy_z=0°;

y_x =90°, y_y=y_z=0°;

Из формулы (2) следует решение обратной задачи: для получения желаемых углов y_x, y_y, y_z углы вращения ОСК следует выбирать из условий:

j_x = y_y (4)

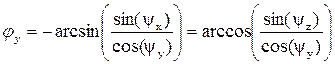
Масштабные коэффициенты осевых искажений (из прямоугольных треугольников):

(5)

Тогда m_x= cos(y_x)£1,

m_y= cos(y_y)£1,

m_z= cos(y_z)£1.

Таким образом, масштабные коэффициенты есть длины отрезков – проекций ортов ОСК на КП. Из формул (1), (3) и (5) следует условие взаимосвязи масштабов:

m²_x+m²_y+m²_z=2. (6)

Это означает, что свободно могут быть выбраны только один или два масштаба.

Иногда нужно обеспечить желаемые соотношения масштабов:

m_x:m_y:m_z = k_x:k_y:k_z.

Тогда, приняв m_i = ck_i, из условия (6) получим:

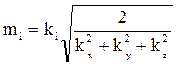
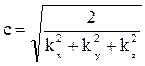(7)

Ориентация проекций осей ОСК на ФКП может быть определена, например, углами g_y, g_xy, g_yz, g_zx, причем g_xy+g_yz+g_zx=360°:

cos (g_y) = m_yy/m_y = cos (j_z) Þ g_y=j_z

(8)

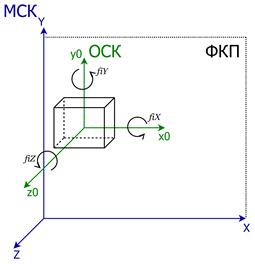
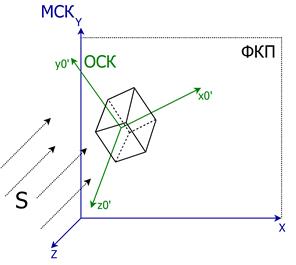
Рис.2. Вращение объекта и его ОСК (fi®j)

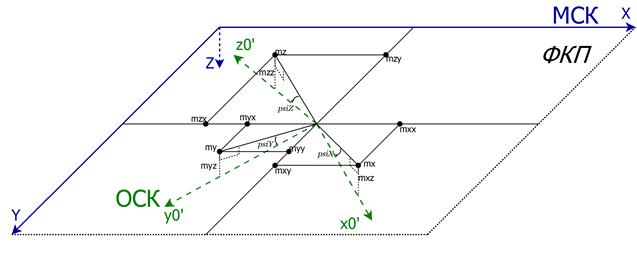
Рис.3. Расчет параметров проекции, углы наклона осей ОСК к ФКП (psi ® y)

Рис.4. Расчет параметров проекции, углы между проекциями осей ОСК (g ® g)

Из анализа данных формул следуют выводы:

1. Только углы j_x и j_y определяют коэффициенты осевых искажений (m_x,m_y,m_z в плоскости проецирования) и углы между проекциями осей ОСК (g_xy,g_yz,g_zx);

2. Только угол j_z последнего поворота ОСК определяет угол g_y вертикальной ориентации проекции ОСК на ФКП. Именно поэтому вращение ОСК вокруг оси z выбрано последним, чтобы было возможно получать разнообразные ракурсы изображения объекта с привычным вертикальным расположением оси y'.

При построении аксонометрической проекции в качестве масштабов m_x,m_y,m_z мы задаемся единичным отрезками на осях x', y' и z'. Таким образом, остальные параметры ортогональной аксонометрической проекции можно рассчитать по вытекающим из (5) формулам:

сos²(j_x) = m_y², сos²(j_y) = (1-m_z²)/m_y²

cos(y_x) = m_x, cos(y_y) = m_y, cos(y_z) = m_z (9)

сos²(g_xy) = (1-m_x²)/(1-m_y²)

сos²(g_yz) = (1-m_y²)/(1-m_z²)

сos²(g_zx) = (1-m_z²)/(1-m_x²)

Полная матрица ортогонального преобразования на ФКП с учетом последней операции проецирования равна (координата z ® 0):

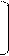
m_xx m_xy 0

A_f = m_yx m_yy 0

m_zx m_zy 0

Элементы матрицы A без последнего вращения (при j_z=0):

m_xx = cos(j_y)cos(j_z) – sin(j_x)sin(j_y)sin(j_z) = cos(j_y)

m_xy = cos(j_y)sin(j_z) + sin(j_x)sin(j_y)cos(j_z) = sin(j_x)sin(j_y)

m_yx = – cos(j_x)sin(j_z) = 0 (10)

m_yy = cos(j_x)cos(j_z) = cos(j_x)

m_zx = sin(j_y)cos(j_z) + sin(j_x)cos(j_y)sin(j_z) = sin(j_y)

m_zy = sin(j_y)sin(j_z) – sin(j_x)cos(j_y)сos(j_z) = – sin(j_x)cos(j_y)

Аксонометрическая проекция окружности p(t) радиуса r, лежащей в плоскости П под углом к КП, равным 90°-y£90°. Ее проекцией является эллипс p'(t) с полуосями a=r и b=rsin(y)£r. Так как координатные плоскости ОСК образуют с ФКП углы 90°-y, то длины и ориентации полуосей эллипсов как проекций окружностей на гранях модельного куба, равны:

a_f=r^z', a_h=r^y', a_p=r^x' (11)

, ,

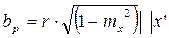
Пример:

Построить аксонометрическую проекцию куба со вписанными в его грани окружностиями при соотношении масштабов m_x:m_y:m_z= 6:5:4.

Решение:

1. Вычисляем по (7):

m_x=6С=0.967

m_y=5С=0.806

m_z=4С=0.645

2. Определим по (8) углы ориентации проекций осей ОСК:

g_xy=101.2° g_yz=150.6° g_zx=108.2°

3. Определим по (11) длины полуосей эллипсов, являющихся фронтальными проекциями окружностей радиуса r на передней, верхней и правой гранях куба:

a_f=a_h=a_p=r

b_f=0.764r, b_h=0.592r b_p=0.255r

4. Для построения изображения необходимо рассчитать углы вращения и матрицу проецирования по (8), (9) и (10):

j_y=-18.4° j_x=36.3° j_z=0°

0.949 -0.187 0

A_f = 0 0.806 0

-0.316 -0.562 0

Таким образом, мы рассмотрели основы аксонометрии – методики построения общей триметрической ортогональной проекции, у которой все осевые масштабы попарно не равны друг другу. Количество триметрических проекций бесконечно, стандартная триметрия отсутствует.

В диметрических проекциях два из трех масштабов равны друг другу, что дает три варианта выбора углов вращения ОСК.

В стандартной диметрической проекции соотношение масштабов составляет 2:2:1.

При построении ортогональной изометрической проекции выбор углов вращения ОСК связан условием равенства всех масштабов.

Алгоритм расчета параметров аксонометрической проекции при заданном соотношении k_x:k_y:k_z и j_z

1. Вычисление m_x:m_y:m_z по (7):

2. Вывод и вычисление j_x, j_y. Из системы (1) и выражений (5):

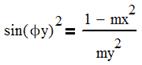
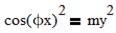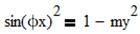
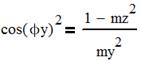
Величина j_z должна быть задана или выбрана, иначе будет бесконечное множество решений.

3. Расчет углов g_y, g_xy, g_yz, g_zx через вычисленные углы j_x, j_y (8). При этом g_y=j_z.

Доп.вопрос: Почему не желательно вычислять через предварительно полученные значения m_xx, m_yx, m_xy, m_yy и т.д.?

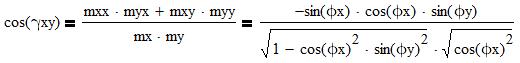
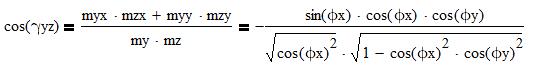
4. Проверка значений углов g_xy, g_yz, g_zx по условию g_xy+g_yz+g_zx=360°. Если условие не соблюдается, необходимо брать другой вариант значений j_x, j_y. Следует учитывать, что при некоторых заданных значениях k_x:k_y:k_z все решения могут оказаться только комплексными.

5. Вычисление элементов матрицы поворота Ryxz и матрицы проецирования A_f (m_xx, m_xy, m_xz, m_yx, m_yy и т.д.) из (1):

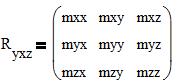
6. Вычисление значений углов наклона осей к плоскости проецирования (y_x, y_y, y_z) из (5) (рис.3):

Дата добавления: 2015-07-13