
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Нормальное распределение
|
|
|
|
11.1. Нормальным называют распределение вероятностей непрерывной случайной величины Х, плотность которого имеет вид:
 ,
,
где а – математическое ожидание, σ – среднее квадратическое
отклонение Х.
11.2.Вероятность того, что Х примет значение, принадлежащее интервалу (α, β):
P(α < x < β) = Ф((β – а) / σ) – Ф((α – а) / σ),
где  – функция Лапласа.
– функция Лапласа.
11.3.Вероятность того, что абсолютная величина отклонения меньше положительного числа δ,
P(│x - a│ < δ) = 2Ф (δ / σ).
В частности, при а = 0 справедливо равенство
P(│x│ < δ) = 2Ф (δ / σ).
Задача 21. Заданы математическое ожидание a и среднее квадратическое отклонение σ нормально распределенной случайной величины Х. Найти: 1) вероятность того, что Х примет значение, принадлежащее интервалу (α, β); 2) вероятность того, что абсолютная величина отклонения Х – а окажется меньше δ.
α = 8, β = 10, a = 6, σ = 2, δ = 0,5 Х-а
Решение.
1) Воспользуемся формулой
P(α < Х < β) = Ф((β – а) / σ) – Ф((α – а) / σ).
Получим
α < Х < β, P(8 < Х <10) = Ф((10 – 6) / 2) – Ф((8 – 6) / 2) = Ф(2) – Ф(1).
По таблице приложения 2 находим Ф(2) = 0,4772 и Ф(1) = 0,3413. Искомая вероятность:
P(8 < Х < 10) = 0,1359.
2) Воспользуемся формулой
P(│Х - a│ < δ) = 2Ф (δ / σ)
Подставив a = 6, σ = 2, δ = 0,5, получим:
P(│Х - 6│ < 0,5) = 2Ф(0,5 / 2) = 2Ф(0,25) = 2 ∙ 0,0987 = 0,1974.
Ответ:
1)Вероятность того, что Х примет значения, принадлежащие интервалу (8, 10), равна 0,1359;
2)Вероятность того, что абсолютная величина отклонения х – а окажется меньше δ, равна 0,1974.
12. ЭЛЕМЕНТЫ МАТЕМАТИЧЕСКОЙ СТАТИСТИКИ
Математическая статистика разрабатывает способы сбора, группировки и анализа статистических данных, т.е. сведений, полученных в результате многократных наблюдений изучаемого явления. Методы математической статистики позволяют решать многие задачи, которые возникают на практике. К их числу относится изучение большой совокупности объектов по небольшому числу случайно отобранных объектов (выборочный метод); нахождение приближенных значений параметров, которыми определяется распределение вероятностей изучаемого признака (статистическая оценка параметров распределения); установление формы и силы связи между случайными величинами (теория корреляции) и др.
В настоящее время методы математической статистики все шире и шире применяются в различных отраслях науки и техники, способствуя их прогрессу. Например, статистические методы используются для правильной и целесообразной организации технологического процесса (предупредительный и приемочный контроль качества продукции), содействуют созданию современной теории точности механизмов; использование этих методов в теоретических исследованиях привело к созданию ряда новых разделов науки (статистическая физика, теория ошибок и др.). Теоретической основой математической статистики является теория вероятностей.
12.1 Точечные оценки
Оценки параметров генеральной совокупности, полученные на основании выборки, называются статистическими. Если статистическая оценка характеризуется одним числом, она называется точечной. К числу таких оценок относится выборочная средняя и выборочная дисперсия.
Выборочная средняя определяется как среднее арифметическое полученных по выборке значений:
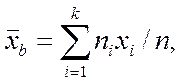
где 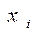 - варианта выборки;
- варианта выборки;
ni - частота варианты;
n - объем выборки.
Замечание. Выборочная средняя будет также обозначаться и без нижнего индекса: 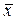 .
.
Выборочная дисперсия представляет собой среднюю арифметическую квадратов отклонений вариант от их выборочной средней:
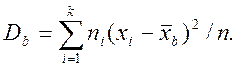


Для расчетов может быть использована также формула
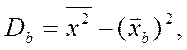
где  - выборочная средняя квадратов вариант выборки.
- выборочная средняя квадратов вариант выборки.
Статистическая оценка является случайной величиной и меняется в зависимости от выборки. Если математическое ожидание статистической оценки равно оцениваемому параметру генеральной совокупности, то такая оценка называется несмещенной, если не равно – то смещенной.
Выборочная средняя является оценкой математического ожидания случайной величины и представляет собой несмещенную оценку. Выборочная дисперсия оценивает дисперсию генеральной совокупности и является смещенной оценкой.
Для устранения смещенности выборочной дисперсии ее умножают на величину n/(n-1) и получают
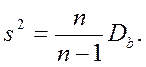
Величину s2 называют несмещенной или «исправленной» выборочной дисперсией.
В некоторых случаях для удобства расчетов при определении статистических оценок переходят к условным вариантам. Например, если варианты xi – большие числа, то используют разность 
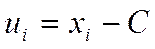 ,
,
где С – произвольно выбранное число (ложный нуль), такое, при котором условные варианты принимают небольшие значения.
В этом случае
 ,
, 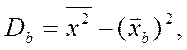


Для изменения значения варианты можно ввести также условные варианты путем использования масштабного множителя:
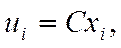
где С =10  (b выбирается положительным или отрицательным целым числом).
(b выбирается положительным или отрицательным целым числом).
Задача 22. Найти выборочную среднюю по данному распределению выборки:
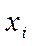
| |||

|
Решение. Так как выборочные значения – большие числа, то целесообразно ввести условные варианты. В качестве ложного нуля выбираем С = 1470 и рассчитываем 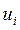 по формуле
по формуле 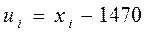 ;
;

| -20 | ||

|
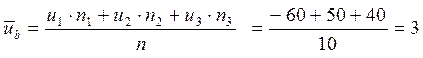 .
.
Определяем выборочную среднюю: 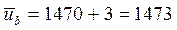 .
.
Ответ:  .
.
Задача 23. Найти несмещенную оценку дисперсии случайной величины Х на основании данного распределения выборки:
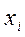 
| ||||

|
Решение. Находим объем выборки и выборочную среднюю
 ;
;

Для вычисления выборочной дисперсии найдем формулу

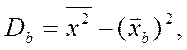
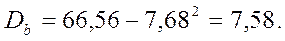
Находим несмещенную оценку дисперсии («исправленную» выборочную дисперсию)

Ответ: 7,73.
12.2 Интегральные оценки
Интегральной называют оценку, которая определяется двумя числами - концами интервала, покрывающего оцениваемый параметр.
Доверительным называют интервал, который с заданной надежностью у покрывает заданный параметр.
Интервальной оценкой (с надежностью  ) математического ожидания
) математического ожидания  нормально распределенного количественного признака X по выборочной средней
нормально распределенного количественного признака X по выборочной средней 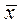 в при известном среднем
в при известном среднем
квадратическом отклонении  генеральной совокупности служит доверительный интервал.
генеральной совокупности служит доверительный интервал.
 b -
b -  <
<  <
<  b +
b + 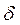 ,
,
где  - точность оценки, n - объем выборки,
- точность оценки, n - объем выборки,
где t - значение аргумента функции Лапласа Ф (t) (см. приложение 1), где Ф (t) = 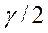 .
.
Задача 24. Заданы среднее квадратическое отклонение 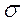 нормально распределенной случайной величины X, выборочная средняя
нормально распределенной случайной величины X, выборочная средняя 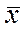 , объем выборки n. Найти доверительный интервал для оценки неизвестного математического ожидания
, объем выборки n. Найти доверительный интервал для оценки неизвестного математического ожидания  с заданной надежностью
с заданной надежностью  = 0,95.
= 0,95.
 = 3,
= 3, 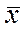 = 18,21, n = 100.
= 18,21, n = 100.
Решение. Воспользуемся формулой  ,тогда 0,95 = 2Ф(t),
,тогда 0,95 = 2Ф(t),
Ф(t) = 0.475. Найдем t=1,96. Вычислим точность оценки

Найдем доверительный интервал для оценки известного математического ожидания а с заданной надежностью 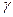 =0,59:
=0,59:
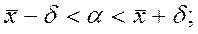
18,21-0,59 <  < 18,21+0,59;
< 18,21+0,59;
17,62 <  < 18,80.
< 18,80.
Ответ:
(17,62;18,80).
13. задачи для контрольных работ.
Студент должен выполнять контрольные работы по варианту, номер которого совпадает с последней цифрой его учебного номера зачётной книжки (шифра).
| Варианты | Номера заданий | ||||||
| 1-10 | 1.1 | 1.2 | 1.3 | 1.4 | 2.1 | 2.2 | |
Контрольная работа состоит из двух заданий. Решения типовых заданий 1.1, 1.2, 1.3 показаны в пункте 18, а образцами выполнения заданий 1.4, 2, 3 соответственно являются: задача 21 – 1.4, задача 23 – 2.1, задача 24 – 2.2.
При выполнении и оформлении контрольных работ необходимо соблюдать следующие правила:
1. В начале работы должны быть ясно написаны фамилия студента, его инициалы, шифр, номер контрольной работы.
2. Контрольная работа выполняется в тетради, а не на листах, обязательно чернилами, с полями для замечаний преподавателя.
3. Решения задач контрольной работы располагаются в порядке номеров, указанных в контрольной работе. Перед решением задачи должно быть полностью записано её условие, исходя из данных своего варианта задания. В том случае, когда несколько задач имеют общую формулировку, переписывая условие задачи, следует заменить общие данные конкретными из своего варианта.
4. Решения задач и объяснения к ним должны быть подробными, аккуратными, без сокращения слов.
Контрольные работы, выполненные студентом с нарушением изложенных правил или не по своему варианту, не зачитываются и возвращаются без проверки.
Получив прорецензированную работу, студент должен исправить в ней все отмеченные ошибки и недочеты. Если работа не зачтена, то в короткий срок либо должна быть выполнена заново, либо должны быть решены задачи, указанные рецензентом.
Исправленную работу следует посылать в университет вместе с незачтенной.
Зачтенные контрольные работы следует предъявить преподавателю на экзамене.
Задание 1.
1.1. В партии из N изделий n из них имеют скрытый дефект (табл. 2). Какова вероятность того, что из взятых наугад m изделий k изделий являются дефектными?
1.2. На сборочное предприятие поступили однотипные комплектующие с трех заводов в количестве: n1 c первого завода, n2 со второго, n3 с третьего (табл. 3). Вероятность качественного изготовления изделий на первом заводе p1, на втором p2, на третьем p3. Какова вероятность того, что взятое случайным образом изделие будет качественным?
1.3. В городе имеются N оптовых баз (табл. 4). Вероятность того, что товар требуемого сорта отсутствует на этих базах, одинакова и равна p. Составить закон распределения числа баз, на которых искомый товар отсутствует в данный момент. Построить многоугольник распределения. Найти дисперсию и среднеквадратичное отклонение числа баз, на которых искомый товар отсутствует в данный момент.
1.4. Непрерывная случайная величина имеет нормальное распределение. Ее математическое ожидание равно a, среднее квадратичное отклонение равно σ (табл. 5). Найти вероятность того, что в результате испытания случайная величина примет значение в интервале (α, β).


Задание 2.
2.1. Найти несмещённую оценку дисперсии случайной величины Х на основании данного распределения выборки (табл.6).
Таблица 6
| Вариант | Распределение | ||||
| xi | |||||
| ni | |||||
| xi | |||||
| ni | |||||
| xi | |||||
| ni | |||||
| xi | 0,2 | 0,3 | 0,5 | 0,6 | |
| ni | |||||
| xi | |||||
| ni | |||||
| xi | –4 | –1 | |||
| ni | |||||
| xi | |||||
| ni | |||||
| xi | –6 | –2 | |||
| ni | |||||
| xi | |||||
| ni | |||||
| xi | –3 | –1 | |||
| ni |
2.2. Заданы среднее квадратическое отклонение σ нормано-распределенной случайной величины Х, выборочная средняя 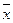 , объем выборки n. Найти доверительные интервалы для оценки неизвестного математического ожидания а с заданной надежностью γ=0,95.
, объем выборки n. Найти доверительные интервалы для оценки неизвестного математического ожидания а с заданной надежностью γ=0,95.
| 1. | σ = 10 | 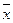 = 18,21 = 18,21
| n = 16 | 6. | σ = 10 | 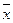 = 18,71 = 18,71
| n = 25 | |
| 2. | σ = 9 | 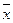 = 18,31 = 18,31
| n = 49 | 7. | σ = 9 | 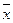 = 18,81 = 18,81
| n = 16 | |
| 3. | σ = 8 | 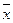 = 18,41 = 18,41
| n = 36 | 8. | σ = 8 | 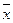 = 18,91 = 18,91
| n = 49 | |
| 4. | σ = 7 | 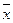 = 18,51 = 18,51
| n =100 | 9. | σ = 7 | 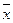 = 20,01 = 20,01
| n = 36 | |
| 5. | σ = 6 | 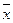 = 18,61 = 18,61
| n = 81 | 10. | σ = 6 | 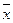 = 20,11 = 20,11
| n = 64 |
14. РЕШЕНИЕ ТИПОВЫХ ЗАДАНИЙ
КОНТРОЛЬНОЙ РАБОТЫ
Задание 1.1
В партии 30 изделий, 10 изделий имеют скрытый дефект. Какова вероятность того, что из взятых наугад пяти изделий три изделия являются дефектными?
Решение. События А –среди отобранных пяти изделий, три изделия являются дефектными.
| 10 деф. | 20 нет | 3 деф. | 2 нет | |
Общее число возможных элементарных исходов события n равно числу способов, которыми можно взять пяти изделий из тридцати, т.е. число сочетаний из тридцати элементов по пять.
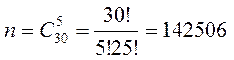 .
.
m - число благоприятствующих исходов событию А определяется  как произведение
как произведение 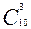 ·
·  , где первый сомножитель указывает число комбинаций выбора деталей с дефектами из десяти. Но с каждой такой комбинацией могут встретиться детали без дефектов. Число комбинаций таких деталей будет
, где первый сомножитель указывает число комбинаций выбора деталей с дефектами из десяти. Но с каждой такой комбинацией могут встретиться детали без дефектов. Число комбинаций таких деталей будет  . Поэтому искомая вероятность запишется в виде
. Поэтому искомая вероятность запишется в виде 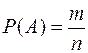 ,
,
Р(А) = 
 = 0,16.
= 0,16.
Ответ: Р (А) = 0,16.
Задание 1.2
На сборочное предприятие поступили однотипные комплектующие с трех заводов в количестве: n1= 20 c первого завода,n2=1,5 со второго, n3=15 с третьего (табл. 3). Вероятность качественного изготовления изделий на первом заводе p1=0,9, на втором p2=0,9, на третьем p3=0,8. Какова вероятность того, что взятое случайным образом изделие будет качественным?
Решение. Задача решается по формуле полой вероятности:
Р(А)=Р(H1) . Р(А/ H1) + Р(H2) . P(A/ H2) + Р(Н3) .Р(A/ Н3).
Событие А - взятое изделие оказалось качественное.
Гипотезы:
H1 - изделие первого завода;
H2 -изделие второго завода;
Н3 - изделие третьего завода.
На завод поступило всего изделий n = n1 + n2 + n3 =50.
Вычислим вероятности данных гипотез
Р(H1) = n1/n =20/50= 0,4; Р(H2)= n2 /n=15/50=0,3;
Р(Н3)= 15/50 = 0,3.
Условные вероятности соответственно равны Р(А/ H1) = p1 = 0,9,
P(A/ H2) = p2 = 0,9, P(A/ Н3) = p3 0,8.
Искомую вероятность того, что взятое изделие окажется качественным, найдем по формуле:
Р(А)=Р(H1) . Р(А/ H1) + Р(H2) . P(A/ H2) + Р(Н3) .Р(A/ Н3) =
=04 . 09+0,3 . 0,8+0,3 . 0,8= 0,84.
Ответ: Вероятность того, что взятое случайным образом изделие, будет качественным, равна 0,84.
Задание 1.3
В городе имеются N=3 оптовых баз. Вероятность того, что требуемого сорта товар отсутствует на этих базах, одинакова и равна p=0,15. Составить закон распределения числа баз, на которых искомый товар отсутствует в данный момент. Построить многоугольник распределения. Найти дисперсию и среднеквадратичное отклонение числа баз, на которых искомый товар отсутствует в данный момент.
Решение. Вычисления будем проводить по формуле Бернулли:
Pn(k) = Ckn. pk . qn-k.
0
p1= P(x=0) =P3 (0) = C3 . p0 . q3 = 1. 1. 0,853 = 0,614,
1
p2 = P(x=1) = P3(1) = C3 . p1 . q2 = 3. 0,15 . 0, 852 = 0,325,
2
p3 = P(x=2) = P3(2) = C3 . p2 . q1 = 3 . 0,152 . 0,85 = 0,0544,
3
p4 = P(x=3) = P3(3) = C3 . p3 . q0= 1. 0,153 . 1 = 0,0034.
Проверим: p1 + p2+ p3+ p4= 0,614 + 0,325 + 0,0574 + 0,0034 =1.
Тогда закон распределения числа баз, на которых искомый товар отсутствует в данный момент, примет вид
| xi | ||||
| pi | 0,6140 | 0,3250 | 0,0574 | 0,0034 |
Вычислим математическое ожидание случайной величины Х иM(X2):
M(X) = x1 .p1 + x2.p2 + x3.p3 + x4.p4 = 0 . 0,61 + 1.0,325 + 2.0,057 + +3.0,0034 = 0,325 + 0,114 + 0,0102 = 0,45,
M(X2) = x12.p1 + x22.p2 + x32.p3 + x42.p4 = 0,325 + 4 .0,057 + 9.0,0034= = 0,553 + 0,0306 = 0,58.
Затем определим дисперсию по формуле
D(X) = M(X2) - (M(X))2 = 0,58 – 0,2 = 0,38.
Среднеквадратичное отклонение равно

 (X) = √ 0,38 = 0,62.
(X) = √ 0,38 = 0,62.
Построим многоугольник распределения (рис.6)


 0,6
0,6

 0,3
0,3

 0,1
0,1
0 1 2 3 
Рис.6
Приложение 1
Таблица значений функции 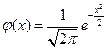
| x | I | |||||||||
| 0,0 | 0,3989 | |||||||||
| 0,1 | ||||||||||
| 0,2 | ||||||||||
| 0,3 | ||||||||||
| 0,4 | ||||||||||
| 0,5 | ||||||||||
| 0,6 | ||||||||||
| 0,7 | ||||||||||
| 0,8 | ||||||||||
| 0,9 | ||||||||||
| 1,0 | 0,2420 | |||||||||
| 1,1 | ||||||||||
| 1.2 | ||||||||||
| 1.3 | ||||||||||
| 1,4 | ||||||||||
| 1,5 | ||||||||||
| 1,6 | ||||||||||
| 1,7 | ||||||||||
| 1,8 | ||||||||||
| 1.9 |
Продолжение приложения 1
| x | I | |||||||||
| 2,0 | 0,0540 | |||||||||
| 2,1 | ||||||||||
| 2,2 | ||||||||||
| 2,3 | ||||||||||
| 2,4 | ||||||||||
| 2,5 | ||||||||||
| 2,6 | ||||||||||
| 2,7 | ||||||||||
| 2,8 | ||||||||||
| 2,9 | ||||||||||
| 3,0 | ||||||||||
| 3,1 | ||||||||||
| 3,2 | ||||||||||
| 3,3 | ||||||||||
| 3,4 | ||||||||||
| 3,5 | ||||||||||
| 3,6 | ||||||||||
| 3,7 | ||||||||||
| 3,8 | ||||||||||
| 3,9 |
Приложение 2
Табличные значения функции 
| x | Ф(х) | x | Ф(x) | x | Ф(x) | x | Ф(x) |
| 0,00 | 0,0000 | 0,23 | 0,0910 | 0,46 | 0,1772 | 0,69 | 0,2549 |
| 0,01 | 0,0040 | 0,24 | 0,0948 | 0,47 | 0,1808 | 0,70 | 0,2580 |
| 0,02 | 0,0080 | 0,25 | 0,0987 | 0,48 | 0,1844 | 0,71 | 0,2611 |
| 0,03 0,04 | 0,0120 0,0160 | 0,26 0,27 | 0,1026 0,1064 | 0,49 0,50 | 0,1879 0,1915 | 0,72 0,73 | 0,2642 0,2673 |
| 0,05 | 0,0199 | 0,28 | 0,1103 | 0,51 | 0,1950 | 0,74 | 0,2703 |
| 0,06 | 0,0239 | 0,29 | 0,1141 | 0,52 | 0,1985 | 0,75 | 0,2734 |
| 0,07 | 0,0279 | 0,30 | 0,1179 | 0,53 | 0,2019 | 0,76 | 0,2764 |
| 0,08 | 0,0319 | 0,31 | О1217 | 0,54 | 0,2054 | 0,77 | 0,2794 |
| 0,09 0,10 | 0,0359 0,0398 | 0,32 0,33 | 0,1255 0,1293 | 0,55 0,56 | 0,2088 0,2123 | 0,78 0,79 | 0,2823 0,2852 |
| 0,11 | 0,0438 | 0,34 | 0,1331 | 0,57 | 0,2157 | 0,80 | 0,2881 |
| 0,12 | 0,0478 | 0,35 | 0,1368 | 0,58 | 0,2190 | 0,81 | 0,2910 |
| 0,13 | 0,0517 | 0,36 | 0,140б | 0,59 | 0,2224 | 0,82 | 0,2939 |
| 0,14 | 0,0557 | 0,37 | 0,1443 | 0,60 | 0,2257 | 0,83 | 0,2967 |
| 0,15 | 0,0596 | 0,38 | 0,1480 | 0,61 | 0,2291 | 0,84 | 0,2995 |
| 0,16 | 0.0636 | 0,39 | 0,I5I7 | 0,62 | 0,2324 | 0,85 | 0,3023 |
| 0,17 | 0,0675 | 0,40 | 0,1554 | 0,63 | 0,2357 | 0,86 | 0,3051 |
| 0,18 | 0,0714 | 0.41 | 0,1591 | 0,64 | 0,2389 | 0,87 | 0,3078 |
| 0,19 | 0,0753 | 0,42 | 0,1628 | 0,65 | 0,2422 | 0,88 | 0,3106 |
| 0,20 | 0,0793 | 0,43 | 0,1664 | 0,66 | 0.2454 | 0,89 | 0,3133 |
| 0,21 0,22 | 0,0832 0,0871 | 0,44 0,45 | 0,1700 0,1736 | 0,67 0,68 | 0,2486 0,2517 | 0,90 0,91 | 0,3159 0,3186 |
Продолжение приложения 2
| x | Ф(х) | X | Ф(х) | X | Ф(х) | x | Ф(x) |
| 0,92 | 0,3212 | 1,18 | 0,3810 | 1,44 | 0,4251 | 1,70 | 0.4554 |
| 0,93 | 0,3238 | 1,19 | 0,3830 | 1,45 | 0.4265 | 1,71 | 0,4564 |
| 0,94 | 0,3264 | 1,20 | 0,3849 | 1.46 | 0,4279 | 1,72 | 0,4573 |
| 0,95 | 0,3289 | 1,21 | 0.3869 | 1,47 | 0,4292 | 1.73 | 0,4582 |
| 0.96 | 0,3315 | 1,22 | 0,3883 | 1,48 | 0,4306 | 1.74 | 0.4591 |
| 0,97 | 0,3340 | 1,23 | 0,3907 | 1,49 | 0,4319 | 1,75 | 0.4599 |
| 0.98 | 0,3365 | 1,24 | 0,3925 | 1,50 | 0,4332 | 1,76 | 0.4608 |
| 0,99 | 0,3389 | 1,25 | 0,3944 | 1,51 | 0,4345 | 1,77 | 0,4616 |
| 1,00 | 0,3413 | 1,26 | 0,3962 | 1,52 | 0,4357 | 1,78 | 0,4625 |
| 1,01 | 0,3438 | 1,27 | 0,3980 | 1,58 | 0,4370 | 1.79 | 0,4633 |
| 1,02 | 0,3461 | 1,28 | 0,3997 | 1,54 | 0,4382 | 1,80 | 0,4641 |
| 1,03 | 0,3485 | 1,29 | 0,4015 | l.55 | 0,4394 | 1,81 | 0,4649 |
| 1,04 | 0,3508 | 1.30 | 0,4032 | 1,56 | 0,4406 | 1.82 | C,4656 |
| 1,05 | 0,3531 | 1.31 | 0,4049 | 1,57 | 0,4418 | 1.83 | 0,4664 |
| 1,06 | 0,3554 | 1,32 | 0,4066 | 1,58 | 0,4429 | 1.84 | 0,4671 |
| 1,07 | 0,3577 | 1,33 | 0,4082 | 1,59 | 0,4441 | 1,85 | 0,4678 |
| 1,08 | 0,3599 | 1,34 | 0,4099 | 1,60 | 0,4452 | 1.86 | 0,4686 |
| 1,09 | 0,3621 | 1,35 | 0,4115 | 1,61 | 0,4463 | 1,87 | 0,4693 |
| 1,10 | 0,3643 | 1,36 | 0,4131 | 1,62 | 0,4474 | 1,88 | 0,4699 |
| 1,11 | 0,3665 | 1,37 | 0,4147 | 1,63 | 0,4484 | 1.89 | 0,4706 |
| I.I2 | 0,3686 | 1.38 | 0,4162 | 1,64 | 0.4495 | 1,90 | 0.4713 |
| 1,13 | 0,3708 | 1,39 | 0,4177 | 1,65 | 0,4505 | 1,91 | 0,4719 |
| 1,14 | 0,3729 | 1,40 | 0,4192 | 1,66 | 0,4515 | 1,92 | 0.4726 |
| 1.15 | 0.3749 | 1,41 | 0,4207 | 1,67 | 0,4525 | 1,93 | 0.4732 |
| 1,16 | 0,3770 | 1,42 | 0.4222 | 1,68 | 0.4585 | 1,94 | 0,4738 |
| 1,17 | 0,3790 | 1,43 | 0.4236 | 1,69 | 0,4545 | 1.95 | 0,4744 |
ОГЛАВЛЕНИЕ
Введение……………………………………………………………3
Основная литература……………………….…………………………….3
Дополнительная литература…………………………………..…...3
1. Основные формулы комбинаторики…………………….……..4
2. Основные понятия теории вероятностей……………….……...5
3. Теоремы сложения и умножения вероятностей………….……9
4. Вероятность появления хотя бы одного события…….………13
5. Формула полной вероятности………………………………....14
6. Формула Бейеса…………………………………………….…..16
7. Формула Бернулли…………………………………………..….17
8. Локальная и интегральная теоремы Лапласа………………....19
9. Вероятность отклонения относительной частоты от теоретической вероятности…………………………………..…..21
10. Случайные величины. Законы распределения. Числовые характеристики случайных величин……………………….………………………………..…...23
11. Нормальное распределение……………………………….…34
12. Элементы математической статистики……………………..35
13. Задачи для контрольных работ……………………………...40
14. Решение типовых заданий контрольной работы…………..43
15. Приложения…………………………………………………..46
|
|
|
|
|
Дата добавления: 2015-07-13; Просмотров: 1765; Нарушение авторских прав?; Мы поможем в написании вашей работы!