Проецирование геометрических тел

Геометрические тела могут быть изображены в системе трех взаимно перпендикулярных плоскостей проек­ций и на одной плоскости (аксонометрическая проекция).

Контуры геометрических тел на любых изображениях задаются проекциями их вершин, ребер, образую­щих, граней и оснований. Таким образом, построение проекций геометриче­ских тел сводится к построению про­екций точек, линий и плоских фигур.

Для различных построений на гео­метрических телах удобно использовать систему прямоугольных коорди­нат, связанную непосредственно с те­лом. Обычно координатные плоскости такой системы совмещают с плоскос­тями симметрии тела и оси координат обозначают на проекциях (рис. 90).

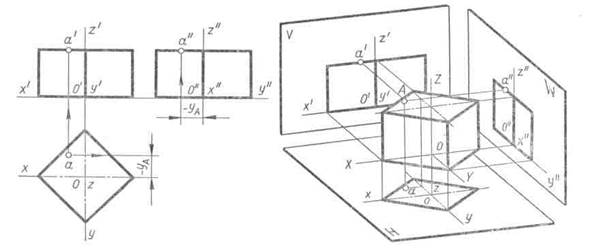
Рис. 90

При построении на поверхности геометрического тела точки или линии вначале ее задают на одной проекции и подразумевают, что она видима (например, на рис. 90 точка А задана на горизонтальной проекции). Затем находят на всех проекциях изображение поверхности, на которой расположена точка (линия), и строят ее недостаю­щие проекции.

Для построения аксонометриче­ских проекций точек, расположенных на поверхности тела, в системе трех плоскостей проекций определяют координаты точки относительно выбран­ной системы координат и последовательно откладывают их на аксономет­рических осях или параллельно им.

Для построения аксонометрической проекции точки, принадлежащей плос­кости уровня, достаточно определить ее координаты в этой плоскости.

Например, изометрическая проекция точ­ки A (рис. 91), расположенной на профиль­ной плоскости (переднее основание призмы), построена по ее координатам — у _А и z _A.

Аксонометрические проекции точек, лежащих на гранях проецирующего или общего положения, строят, ис­пользуя вспомогательные прямые, ко­торые проводят на гранях через задан­ные точки. Вспомогательная прямая придает изображению точки большую наглядность, так как четко устанавли­вает принадлежность ее определенной грани.

На рис. 91 построена изометрическая про­екция точки В, расположенной на профильно проецирующей плоскости (боковая грань призмы). Вначале откладывают по оси Y от точки O координату у _В и через ее конец проводят пря­мую, параллельную оси Z. На пересечении этой прямой с ребром основания призмы полу­чают точку, высота которой равна координате z _В. Через эту точку проводят в плоскости боко­вой грани прямую, параллельную оси X, и на ней откладывают координату х _В.

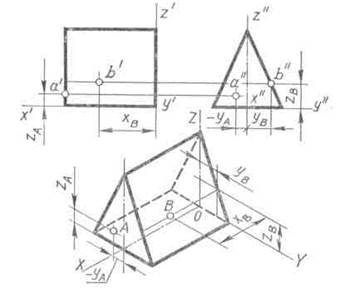
Рис. 91

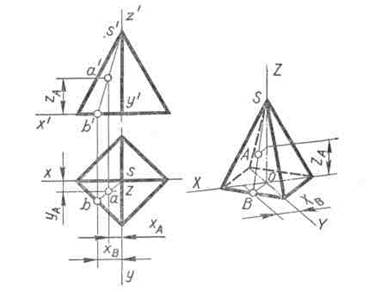
Рис. 92

Примером точки, лежащей на гра­ни, занимающей общее положение, служит точка А (рис. 92). Она по­строена в диметрической проекции на вспомогательной прямой SB, прове­денной через указанную точку на гра­ни пирамиды.

Для построения диметрической проекции прямой SB по оси X откладывают координату х _В и через ее конец проводят прямую, параллельную оси Y. На пересечении ее с ребром основания получают точку В и проводят пря­мую SB. Далее, соединив точки В и О, получают диметрическую проекцию прямоугольного треугольника SOB,и приступают к построению точки A. Для этого по оси Z откладывают координату z _А и через се конец проводят пря­мую, параллельную катету ОВ, и продолжают ее до пересечения с гипотенузой SB в точке A.

Аксонометрические проекции точек, расположенных на цилиндрической поверхности, строят с помощью обра­зующих цилиндра.

Через заданную точку, например A, про­водят образующую (рис. 93) и строят ее диметрическую проекцию по координатам х _А и у _A. Затем от основания цилиндра на этой об­разующей откладывают координату z_А и получают точку А.

Для построения аксонометрических проекций точек, лежащих на поверх­ности конуса, также используют его образующие.

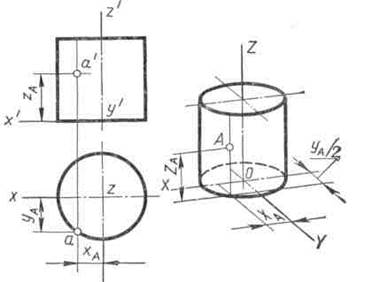
Рис. 93

Рис. 94

Например, для построения изометрической проекции точки А (рис. 94) использована образующая SB. Последовательность построений изометрической проекции точки А аналогична построению диметрической проекции одноимен­ной точки на рис. 92.

Для переноса с проекций на раз­вертку точки или линии необходимо на обоих изображениях обозначить реб­ра (у многогранников) или образую­щие (у тел вращения), чтобы пра­вильно поместить заданные точки (от­резки) на развертке.

На рис. 95 показан перенос ломаной линии 1 — 2 — 3 — 4, расположенной на боковой поверхности шестиугольной пирамиды, с проекций на развертку. Точки 1, 4 и 2 лежат на ребрах пирамиды, которые проецируются без искажения на плоскость H (ребра AF и ВС) или V (ребро SA). Поэтому на горизонтальной проекции замеряют отрезки L₁=а1 и L₄ = c4, a на фронтальной — отрезок L₂ = s'2' и перено­сят их на соответствующие ребра развертки. Точка 3 лежит на ребре SB, занимающем об­щее положение. Для определения длины отрез­ка L₃ ребро SB вместе с точкой 3 поворачива­ют вокруг высоты пирамиды до положения, параллельного плоскости V, т е до совмеще­ния с ребром SD (или SA). Затем на фронталь­ной проекции замеряют отрезок L₃ = s'3₁ и пе­реносят его на развертку.

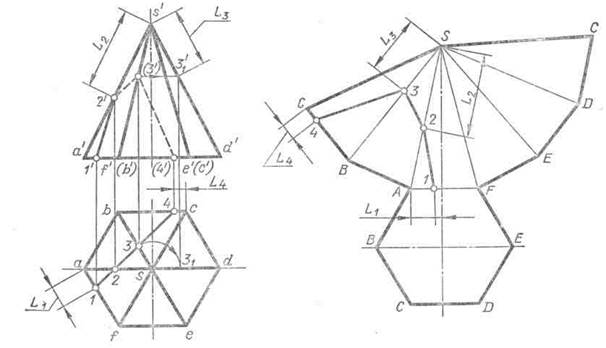
Рис. 95

Если точка расположена на грани многогранника или на боковой поверх­ности тела вращения, то на развертке ее строят с помощью той вспомога­тельной линии, которая была исполь­зована для построения проекций точки.

Например, точка А (рис. 96), принадлежа­щая конической поверхности, на проекции и на развертке изображена на образующей SB. Сначала на развертке строят образующую SB с помощью хорды L_B. Затем поворачивают точку A вокруг оси конуса до совмещения ее на фронтальной проекции с очерковой образующей конуса. Далее замеряют длину отрезка L_A = s'a₁ и, отложив его на образующей SB, по­лучают изображение точки A на развертке.

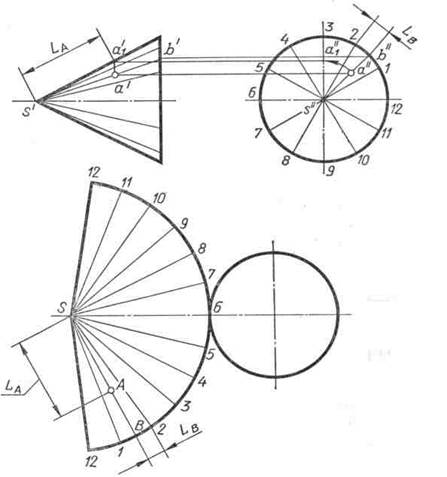
Рис. 96

При тренировке на чтение проек­ций геометрического тела, т. е. на представление по проекциям его формы в це­лом и умение видеть на любой проекции от­ дельные его элементы: точки, линии (прямые,
дуги, лекальные кривые), плоские фигуры, рекомендуется выделять искомые элементы геометрических тел цветными карандашами. При этом следует
различать проекции ви­димых и невидимых элементов. Обозначение проекций невидимых точек заключают в скобки, а невидимые
линии изображают штриховыми линиями.

	Рис. 98
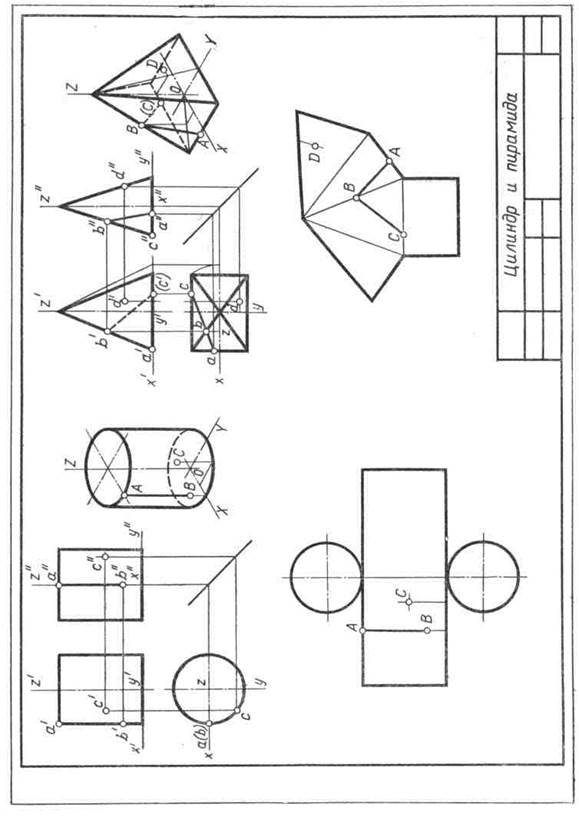
	Рис. 99

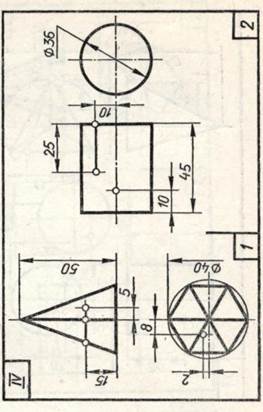
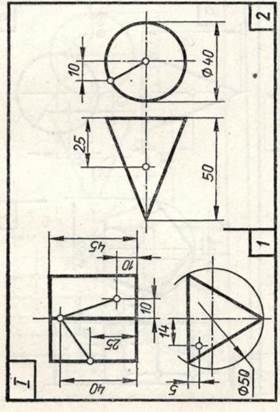
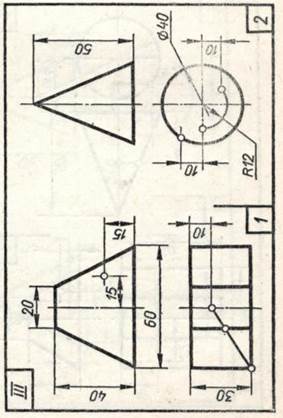
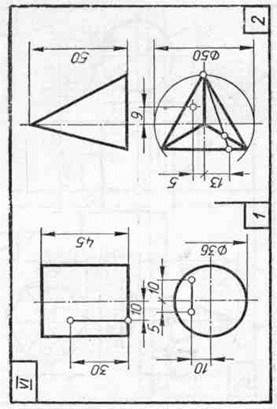
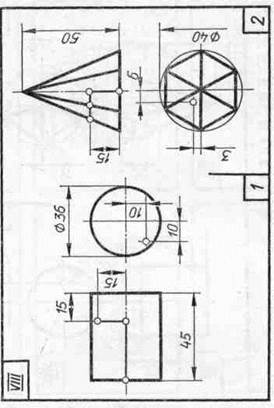
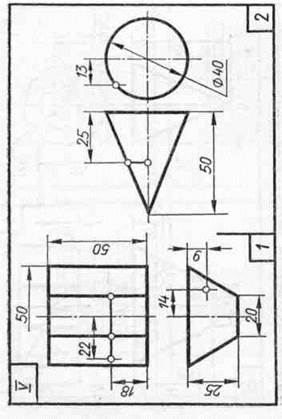
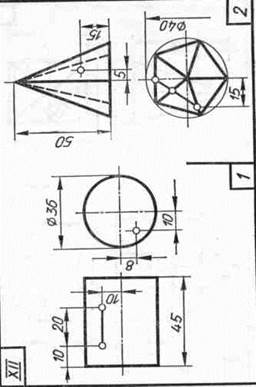
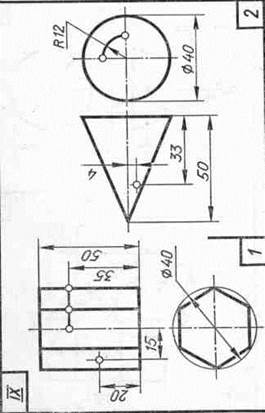
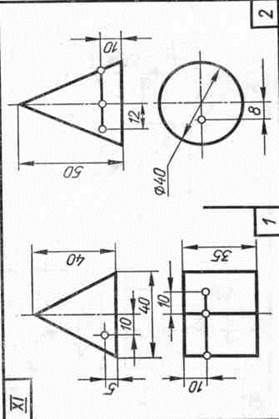
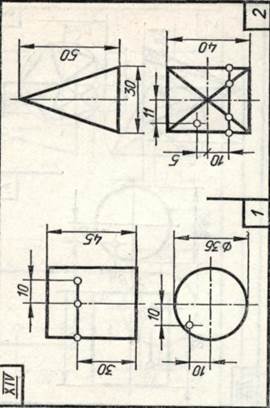
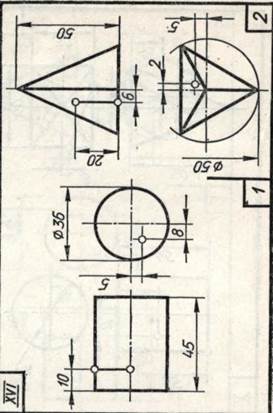
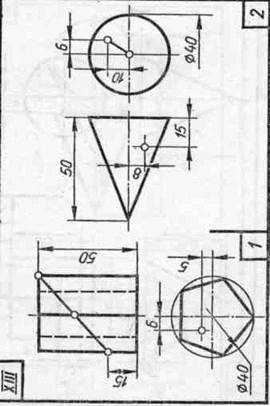
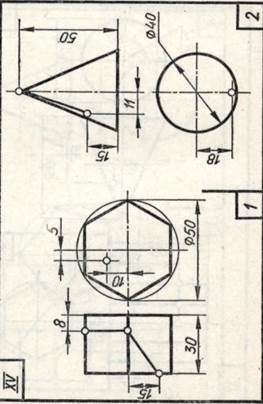
Задание 20. Геометрические тела. Построить два заданных геометрических тела в системе трех плоско­стей проекций и в изометрической про­екции, а также их развертки, и на всех изображениях определить про­екции заданных точек и линий.

Образцы выполненного задания приведены на рис. 98 и 99. При их выполнении рекомендуется на левой половине листа помещать изображе­ния призмы или цилиндра, а на пра­вой — пирамиды или конуса.

В задании для каждого геометри­ческого тела предусмотрено несколько изображений, поэтому их компоновке на поле чертежа следует уделить особое внимание. На законченных изо­бражениях вспомогательные построения можно сохранить, а проекции за­данных точек и линий выделить цвет­ными карандашами.

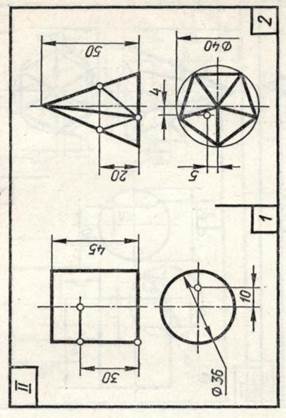
Дата добавления: 2015-07-13