Механические колебания 1 страница

Законы сохранения в механике

Материальный объект в любой момент времени характеризуется определенными величинами – параметрами состояния. Задать механическое состояние системы - это, значит, задать его параметры.

Не все физические величины являются параметрами состояния. Ряд величин характеризует не состояние системы, а процесс перехода системы из одного состояния в другое, в течение некоторого времени. Например, энергия – параметр, а механическая работа – характеризует переход системы из одного состояния в другое и параметром не является.

При решении задач надо выбрать два или более таких состояния системы, чтобы в число их параметров входили как известные, так и неизвестные величины. Как правило, одно состояние берется до взаимодействия, а второе после.

Следует помнить, что для определения потенциальной энергии системы вначале необходимо выбрать нулевой уровень энергии (начало отсчета).

Применяя закон сохранения импульса надо помнить, что может сохраняться не только импульс, но и проекция импульса на некоторое направление, если сумма сил, действующих на тело в этом направлении, равна нулю.

При упругом взаимодействии выполняются законы сохранения импульса и энергии, а при неупругом только импульса.

Если система уравнений оказывается неполной, необходимо совместное применение законов сохранения импульса и энергии.

Обратим внимание на то, что в поступательном движении сохраняется импульс, то во вращательном движении – момент импульса.

Пусть некоторая величина 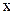, описывающая состояние системы, описывается уравнением вида 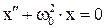, где 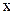- упомянутая величина, а 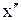- ее вторая производная по времени, 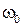- собственная частота колебаний.. Тогда говорят, что система совершает гармонические колебания, описываемые уравнением .

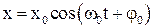Достаточным условием возникновения колебаний является появление, после выведения системы из положения равновесия, возвращающей силы, пропорциональной смещению системы от положения равновесия, так называемой квазиупругой силы 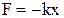. Система, совершающая колебания под действием квазиупругой силы, называется одномерным гармоническим осциллятором.

Если в системе действует сила сопротивления, пропорциональная скорости 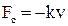, то в этом случае уравнение имеет вид 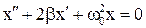, а его решение 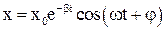описывает затухающие колебания с частотой 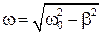, которая называется частотой свободных колебаний.

Затухание колебаний характеризуют логарифмическим декрементом 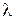и добротностью системы .

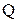Логарифмический декремент затухания обратен промежутку времени в течении которого амплитуда колебаний уменьшается в «е» раз.

Добротность системы характеризует потери энергии в системе на преодоление сил трения, 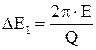, где - потери энергии за одно полное колебание, а 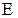- начальное значение энергии системы.

Резонансная частота определяется выражением и если выполняется условие 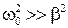можно считать, .

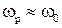Чтобы получить уравнение траектории точки при сложении колебаний нужно из уравнений движения 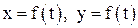исключить время. В случае различных частот колебаний траектория определяется геометрическим способом. Для этого надо рассчитать несколько (10 – 20) значений 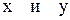и по полученным данным построить траекторию точки.

ПОСЛЕКУРСОВОЕ ЗАДАНИЕ

Таблица вариантов

Вариант	Номера задач
	1,15,26,40,46,60,66,72,92,106,118,126,140,146,170,185
	2,16,27,41,47,61,67,73,93,107,119,127,141,147,169,184
	3,17,28,42,48,62,68,74,94,108,120,128,142,148,168,183
	4,18,29,43,49,63,69,75,95,109,121,129,143,149,167,182
	5,19,30,44,50,64,70,76,96,110,122,130,144,150,166,181
	6,20,31,45,51,65,71,77,97,111,123,131,145,151,165,180
	7,21,32,44,52,64,70,78,98,112,124,132,144,152,164,179
	8,22,33,43,53,63,69,79,99,113,125,133,143,153,163,178
	9,23,34,42,54,62,68,80,100,114,124,134,142,154,162,177
	10,24,35,41,55,61,67,81,101,115,123,135,141,155,161,176
	11,25,34,40,54,60,66,82,102,114,122,134,140,154,160,175
	12,24,33,39,53,59,67,83,103,113,121,135,139,153,159,174
	13,23,32,38,52,58,68,84,104,112,120,132,138,152,158,173
	14,22,31,37,51,57,69,85,105,111,119,131,137,151,157,172
	13,21,30,36,50,56,70,86,104,110,118,130,136,150,156,171

1. Движение материальной точки задано уравнением: 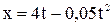. Определить момент времени, в который скорость точки равна нулю. Найти координату и ускорение точки в этот момент.

2. Движение двух материальных точек задано уравнениями: 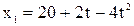, 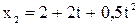. В какой момент времени скорости точек будут одинаковы? Определить расстояние между точками в этот момент времени.

3. Две материальные точки движутся согласно уравнениям: 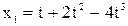, 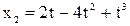. В какой момент времени ускорения точек будут одинаковы? Найти скорости точек в этот момент времени.

4. Движение точки по прямой задано уравнением 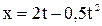. Определить среднюю скорость движения точки в интервале времени от 1 до 3 с.

5. Движение точки по прямой задано уравнением 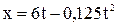. Определить среднюю скорость движения точки в интервале времени от 2 до 6 с.

6. Движение точки по прямой задано уравнением 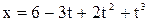. Определить для точки в интервале времени от 1 до 4 с среднюю скорость и среднее ускорение.

7. Движение точки по прямой задано уравнением 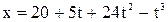. В какой момент времени ускорение точки равно нулю? Определить скорость точки в этот момент времени.

8. Точка движется по прямой согласно уравнению: 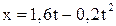. Определить среднюю скорость точки в интервале от 2 до 6 с.

9. Материальная точка движется прямолинейно согласно уравнению 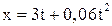. Каковы средние значения скорости и ускорения за первые 3 с движения?

10. Точка движется по прямой согласно уравнению: 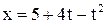. Определить среднюю скорость точки в интервале от 1 до 6 с.

11. Точка движется по прямой согласно уравнению: 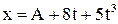. Через сколько времени после начала движения ускорение точки будет равно 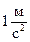. Чему равно среднее ускорение точки за это время?

12. Движение точки по прямой задано уравнением 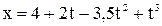. Определить среднюю скорость движения точки в интервале времени от 1 до 3 с.

13. Движение точки по прямой задано уравнением 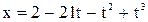. Определить среднюю скорость движения точки в интервале времени от 2 до 4 с.

14. Движение точки по прямой задано уравнением 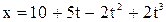. Определить для точки в интервале времени от 1 до 4 с среднюю скорость и среднее ускорение.

15. Диск радиусом 20 см вращается согласно уравнению 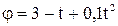. Определить тангенциальное, нормальное и полное ускорение точек на окружности диска для момента времени .

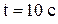16. Движение точки по окружности радиусом 4 м задано уравнением 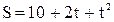. Найти тангенциальное, нормальное и полное ускорение точки для момента времени .

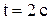17. Движение точки по окружности радиусом 0,2 м задано уравнением 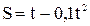. Найти тангенциальное, нормальное и полное ускорение точки для момента времени .

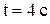18. Колесо вращается с постоянным угловым ускорением 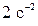. Через 0,5 с после начала движения полное ускорение точки на ободе колеса стало равно 0,136 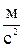. Найти радиус колеса.

19. Диск радиусом 20 см вращается согласно уравнению 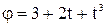. Определить тангенциальное, нормальное и полное ускорение точки, находящейся на расстоянии 0,1 м от оси вращения, для момента времени .

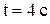20. Точка движется по окружности радиусом 0,2 м с постоянным тангенциальным ускорением 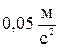. Через сколько времени после начала движения нормальное ускорение точки будет равно тангенциальному?

21. Точка движется по окружности радиусом 2 м согласно уравнению . В какой момент времени нормальное ускорение точки будет равно ее тангенциальному ускорению? Определить полное ускорение точки в этот момент.

22. Точка движется по окружности, согласно уравнению 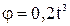. В какой момент времени нормальное ускорение точки будет равно ее тангенциальному ускорению? Определить полное ускорение точки в этот момент.

23. Найти угловое ускорение колеса, если известно, что через 2 с после начала движения, вектор полного ускорения образует угол 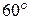с направлением вектора линейной скорости этой точки.

24. Диск вращается вокруг горизонтальной оси согласно уравнению 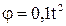. Определить полное ускорение точки на ободе диска к концу второй секунды после начала движения, если линейная скорость этой точки в этот момент равна .

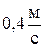25. Диск радиусом 10 см, находившийся в состоянии покоя, начал вращаться с постоянным угловым ускорением 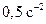. Найти тангенциальное, нормальное и полное ускорение точки на окружности диска в конце второй секунды после начала движения.

26. Движение точки задано уравнениями: 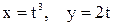. Найти уравнение траектории точки, ее скорость и полное ускорение в момент времени .

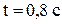27. Движение точки задано уравнениями: 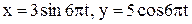. Найти уравнение траектории точки, ее скорость и полное ускорение в момент времени .

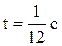28. Движение точки задано уравнениями: 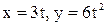. Найти уравнение траектории точки, ее скорость и полное ускорение в момент времени .

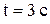29. Движение точки задано уравнениями: 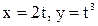. Найти уравнение траектории точки, ее скорость и полное ускорение в момент времени .

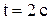30. Движение точки задано уравнениями: 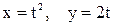. Найти уравнение траектории точки, ее скорость и полное ускорение в момент времени .

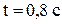31. Движение точки задано уравнениями: 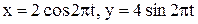. Найти уравнение траектории точки, ее скорость и полное ускорение в момент времени .

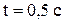32. Движение точки задано уравнениями: 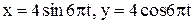. Найти уравнение траектории точки, ее скорость и полное ускорение в момент времени .

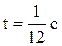33. Движение точки задано уравнениями: 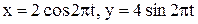. Найти уравнение траектории точки, ее скорость и полное ускорение в момент времени .

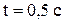34. Движение точки задано уравнениями: 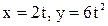. Найти уравнение траектории точки, ее скорость и полное ускорение в момент времени .

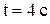35. Движение точки задано уравнениями: 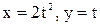. Найти уравнение траектории точки, ее скорость и полное ускорение в момент времени .

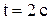36. На тело массой m, лежащее на горизонтальной плоскости, действует сила F под углом 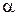к горизонту. Сила приложена к центру масс, коэффициент трения 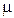. Найти ускорение тела, если оно не отрывается от плоскости.

37. Сила сопротивления воздуха, действующая на капли тумана, прямо пропорциональна произведению радиуса капли на ее скорость. Капли радиусом 0,1 мм имеют у земли скорость 1 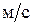. Какую скорость будут иметь у земли капли, радиус которых в 10 раз меньше?

38. Тело скользит по наклонной плоскости, составляющей с горизонтом угол 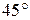. Пройдя расстояние 36,4 см, тело приобретает скорость 2 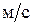. Чему равен коэффициент трения тела о плоскость?

39. Масса автомобиля 1 т, коэффициент сопротивления движению 0,1. Найти силу тяги, развиваемую мотором автомобиля, если он движется в гору с углом наклона 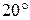с ускорением .

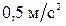40. К концам нити, перекинутой через неподвижный блок, подвешены грузы массой 2 и 3 кг. Определить ускорение грузов и силу натяжения нити, если ось блока движется вверх с ускорением .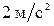

41. Гирька, привязанная к нити длиной 30 см, описывает в горизонтальной плоскости окружность диаметром 30 см. Какова частота обращения гирьки?

42. На тело массой 10 кг, лежащее на наклонной плоскости с углом наклона 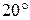, действует горизонтально направленная сила 8 Н. Пренебрегая трением, определить ускорение, с которым движется тело.

43. С вершины наклонной плоскости, длиной 2 м и высотой 1 м начинает соскальзывать тело. Коэффициент трения между телом и плоскостью 0,15. Определить ускорение тела и время движения по наклонной плоскости.

44. Два груза массой 5 и 7 кг связаны нитью и лежат на горизонтальной плоскости. К одному из грузов приложена сила 60 Н. Пренебрегая трением, определить ускорение грузов и силу натяжения нити. Изменится ли ответ, если силу приложить к другому грузу?

45. Какой угол с горизонтом составляет поверхность бензина в баке автомобиля, движущегося горизонтально с ускорением ?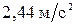

46. Тонкий обруч радиусом 0,5 м раскрутили вокруг его оси до угловой скорости 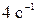и положили на стол. Через какое время обруч остановится, если коэффициент трения между столом и обручем равен 0,2?

47. Определить момент силы, который надо приложить к блоку в форме цилиндра радиусом 20 см, вращающемуся с частотой 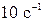, чтобы он остановился в течение 20 с. Масса блока 12 кг.

48. По касательной к шкиву маховика в виде диска диаметром 75 см и массой 40 кг приложена сила 1 кН. Определить угловое ускорение и частоту обращения маховика через 10 с после начала движения, если радиус шкива 12 см. Трение не учитывать.

49. Определить момент силы, который необходимо приложить к блоку, вращающемуся с частотой 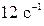, чтобы он остановился в течение 8 с. Диаметр блока 30 см. Массу блока 6 кг считать равномерно распределенной по ободу.

50. Маховик в виде сплошного диска радиусом 0,2 м и массой 50 кг раскручен до частоты вращения 480 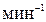и предоставлен самому себе. Под действием сил трения маховик остановился через 50 с. Определить момент сил трения.

51. По касательной к ободу маховика в виде диска диаметром 60 см и массой 20 кг приложена сила. Определить величину этой силы, если через 1 мин после начала движения частота вращения маховика стала равна .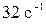

52. Определить момент силы, который необходимо приложить к блоку, вращающемуся с частотой 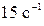, чтобы он остановился в течение 20 с? Массу блока 4 кг считать равномерно распределенной по диску.

53. Тонкий однородный стержень длиной 50 см и массой 400 г вращается с угловым ускорением 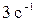около оси, проходящей через его центр. Определить вращающий момент, действующий на стержень.

54. На обод маховика диаметром 60 см намотан шнур, к концу которого привязали гирю массой 2 кг. Определить момент инерции маховика, если он, вращаясь под действием силы натяжения шнура за 3 с, приобрел угловую скорость .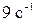

55. Однородный диск радиусом 0,2 м и массой 5 кг, вращается вокруг оси, проходящей через его центр по закону 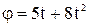. Найти величину силы, действующей на диск.

56. На горизонтальную ось насажен маховик и легкий шкив радиусом 15 см. На шкив намотан шнур, к свободному концу которого привязан груз массой 0,4 кг. Определить момент инерции маховика, если груз движется с ускорением .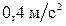

57. Через неподвижный блок массой 0,2 кг перекинут шнур, к концам которого подвешены грузы массой 0,3 и 0,5 кг. Определить силы натяжения шнура по обе стороны блока во время движения грузов. Массу блока считать равномерно распределенной по ободу.

58. Через неподвижный блок в виде однородного диска массой 0,2 кг перекинута нить, к концам которой привязаны грузы массой 0,35 и 0,55 кг. Определить отношение сил натяжения нити по обе стороны блока.

59. На однородный сплошной цилиндрический вал радиусом 20 см, момент инерции которого 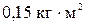, намотана легкая нить, к концу которой прикреплен груз массой 0,5 кг. Определить силу натяжения нити.

60. На однородный сплошной цилиндрический вал радиусом 0,5 м намотана легкая нить, к концу которой прикреплен груз массой 6,4 кг. Груз, разматывая нить, движется с ускорением 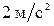. Определить момент инерции вала.

61. К ободу колеса, имеющего форму диска, радиусом 0,5 м и массу 50 кг приложена сила 100 Н. Через сколько времени частота вращения колеса станет равна ?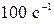

62. Через блок в виде сплошного диска, имеющего массу 80 г, перекинута тонкая нить, к концам которой подвешены грузы массой 100 и 200 г. Определить ускорение грузов.

63. Сплошной цилиндр массой 5 кг насажен на горизонтальную ось. На цилиндр намотана нить, к свободному концу которой подвешена гиря массой 10 кг. С каким ускорением будет опускаться гиря, если ее отпустить?

64. На ступенчатый блок с радиусами 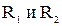, причем 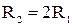, намотаны в противоположных направлениях две легкие нити, нагруженные массами 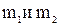. Найти ускорения грузов и силу натяжения нитей, если момент инерции блока равен I.

65. Блок, имеющий форму диска массой 0,4 кг, вращается под действием силы натяжения нити, к концам которой подвешены грузы массой 0,3 и 0,7 кг. Определить силу натяжения нити по обе стороны блока.

66. При движении в воздухе скорость пули массой 10 г уменьшилась с 800 до 200 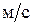. Считая силу сопротивления пропорциональной квадрату скорости, определить коэффициент пропорциональности. Действием силы тяжести можно пренебречь. Время движения пули 0,8 с.

67. Катер массой 2 т трогается с места и в течение 10 с развивает скорость 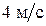. Определить силу тяги мотора считая ее постоянной. Принять силу сопротивления движению пропорциональной скорости. Коэффициент пропорциональности равен 100 .

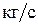68. Снаряд массой 10 кг выпушен вертикально вверх с начальной скоростью 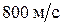. Считая силу сопротивления воздуха пропорциональной скорости, определить время подъема снаряда до высшей точки. Коэффициент сопротивления равен 0,25 .

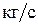69. Моторная лодка массой 400 кг начинает двигаться из состояния покоя. Сила тяги двигателя 200 Н. Считая силу сопротивления пропорциональной скорости, определить скорость лодки через 20 с после начала движения. Коэффициент сопротивления равен 20 .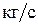

70. Катер массой 2 т трогается с места и в течение 10 с развивает скорость 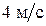. Определить силу тяги мотора считая ее постоянной. Принять силу сопротивления движению пропорциональной скорости. Коэффициент пропорциональности равен 100 .

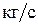71. Катер массой 2 т с двигателем мощностью 50 кВт развивает максимальную скорость 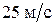. Определить время, в течение которого катер после выключения двигателя потеряет половину своей скорости. Принять, что сила сопротивления движению катера прямо пропорциональна квадрату скорости.

72. В лодке массой 240 кг стоит человек массой 60 кг. Лодка плывет со скоростью 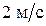. Человек прыгает с лодки в горизонтальном направлении со скоростью 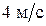(относительно лодки). Найти скорость движения лодки после прыжка человека, если человек прыгает в сторону, противоположную движению лодки.

73. На полу стоит тележка в виде длинной доски, снабженной легкими колесами. На одном конце доски стоит человек. С какой скоростью (относительно пола) будет двигаться тележка, если человек пойдет вдоль нее со скоростью (относительно доски) . Масса тележки 20 кг, масса человека 60 кг.

74. Человек массой 60 кг, бегущий со скоростью 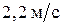, догоняет тележку массой 80 кг, движущуюся со скоростью 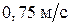и вскакивает на нее. С какой скоростью будет двигаться тележка?

75. Снаряд массой 10 кг обладал скоростью 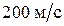в верхней точке траектории. В этой точке он разорвался на две части. Меньшая часть массой 3 кг получила скорость 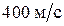в прежнем направлении. Найти скорость второй, большей части после разрыва.

76. На катере массой 4,5 т находится водомет, выбрасывающий со скоростью 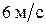относительно катера воды. Пренебрегая сопротивлением движению катера, определить максимальную скорость катера.

77. Лодка массой 150 кг и длиной 2,8 м стоит неподвижно в стоячей воде. Человек массой 90 кг в лодке переходит с носа на корму. Пренебрегая сопротивлением воды, определить, на какое расстояние при этом переместится лодка.

78. Платформа с песком массой 2 т стоит на рельсах на горизонтальном участке пути. В платформу попадает снаряд массой 8 кг и застревает в ней. Определить скорость платформы после удара, если в момент попадания скорость снаряда 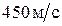, а ее направление – сверху вниз под углом к горизонту. Трением пренебречь.

79. На платформе, движущейся со скоростью 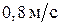, укреплено орудие. Масса платформы 10 т. Ствол орудия направлен в сторону движения платформы. Снаряд массой 10 кг вылетает из ствола орудия под углом 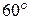к горизонту. Определить скорость снаряда, если после выстрела скорость платформы уменьшилась в два раза.

80. Горизонтальная платформа массой 25 кг и радиусом 0,8 м вращается с частотой 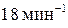. В центре стоит человек и держит в расставленных руках гири. Считая платформу диском, определить частоту вращения платформы, если человек, опустив руки, уменьшит свой момент инерции от 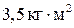до .

Дата добавления: 2015-07-13