Механические колебания 2 страница

81. Две тележки массой каждая движутся без трения друг за другом со скоростью 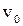. Человек массой 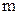, находящийся на задней тележке, прыгнул на переднюю со скоростью относительно своей тележки. Определить скорость передней тележки после прыжка человека.

82. Человек, стоящий на скамье Жуковского, держит в руках стержень длиной 2,5 м и массой 8 кг, расположенный вертикально вдоль оси вращения скамейки. Эта система обладает моментом инерции и вращается с частотой 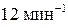. Определить частоту вращения системы, если стержень повернуть в горизонтальное положение.

83. Человек массой 60 кг, стоящий на краю горизонтальной платформы массой 120 кг, вращающейся вокруг неподвижной вертикальной оси с частотой , переходит к ее центру. Считая платформу диском, а человека материальной точкой, определить с какой частотой будет вращаться платформа.

84. Человек массой 60 кг, стоящий в центре горизонтальной платформы массой 120 кг, вращающейся вокруг неподвижной вертикальной оси с частотой , переходит к ее краю. Считая платформу диском, а человека точкой, определить с какой частотой будет вращаться платформа.

85. На краю платформы в виде диска стоит человек, масса которого в 3 раза меньше массы платформы. Определить во сколько раз увеличится угловая скорость вращения платформы, если человек перейдет ближе к центру на расстояние, равное половине радиуса платформы.

86. Человек стоит на скамье Жуковского и ловит рукой мяч массой 0,4 кг, летящий в горизонтальном направлении со скоростью 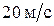. Траектория мяча проходит на расстоянии 0,8 м от оси вращения. С какой угловой скоростью начнет вращаться скамья, если момент инерции ее равен .

87. Человек массой 60 кг, стоящий на краю горизонтальной платформы радиусом 1 м и массой 120 кг, вращающейся вокруг неподвижной вертикальной оси с частотой , переходит к ее центру. Считая платформу однородным диском, а человека материальной точкой, определить работу, совершенную при этом человеком.

88. Платформа массой 240 кг, имеющая форму диска, может вращаться вокруг вертикальной оси. На краю платформы стоит человек массой 60 кг. С какой угловой скоростью будет вращаться платформа, если человек пойдет вдоль нее со скоростью 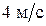относительно платформы.

89. Человек массой 60 кг, стоящий на краю горизонтальной платформы радиусом 1 м и массой 120 кг, вращающейся вокруг неподвижной вертикальной оси с частотой , переходит к ее центру. Считая платформу однородным диском, а человека материальной точкой, определить работу, совершенную при этом человеком.

90. Человек стоит на неподвижной скамье Жуковского и бросает мяч массой 0,5 кг со скоростью 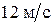направленной в горизонтальном направлении. Траектория мяча проходит на расстоянии 0,6 м от оси вращения. С какой угловой скоростью начнет вращаться скамья вместе с человеком, если суммарный момент инерции человека и скамьи равен ?

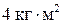91. Платформа, имеющая форму диска, может вращаться около вертикальной оси. На краю платформы стоит человек массой 60 кг. На какой угол повернется платформа, если человек пойдет вдоль края платформы и, обойдя ее, вернется в исходную точку. Масса платформы 240 кг.

92. С верхней точки полусферы соскальзывает без трения маленькая шайба. На какой высоте шайба оторвется от полусферы, если ее радиус равен 60 см?

93. Шар скатывается без проскальзывания с наклонной плоскости высотой 90 см. Какую линейную скорость будет иметь центр шара в тот момент, когда шар скатиться с наклонной плоскости?

94. Пуля массой 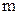, летящая горизонтально со скоростью , попадает в ящик с песком массой , подвешенный на нити длиной 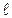и застревает в нем. Определить на какой угол от вертикали отклонится при этом нить?

95. Груз массой 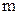, подвешен на пружине с жесткостью 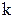, находится на подставке. Пружина при этом не деформирована. Подставку быстро убирают. Определить максимальное удлинение пружины и максимальную скорость груза.

96. Цилиндр скатывается без трения с наклонной плоскости высотой 1,2 м. Какую линейную скорость будет иметь центр цилиндра в тот момент, когда цилиндр скатится с наклонной плоскости?

97. Однородный стержень длиной 1 м и массой 0,7 кг подвешен на горизонтальной оси, проходящей через верхний конец стержня. В точку, отстоящую от оси на длины, стержня абсолютно неупруго попадает пуля массой 5 г, летящая горизонтально перпендикулярно стержню и его оси. После удара стержень отклоняется на угол 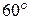. Найти скорость пули.

98. Карандаш длиной 20 см, поставленный вертикально, падает на стол. Какую линейную скорость будет иметь в конце падения верхний конец карандаша?

99. Однородный стержень длиной 85 см подвешен на горизонтальной оси, проходящей через верхний конец стержня. Какую горизонтальную скорость нужно сообщить нижнему концу стержня, чтобы он сделал полный оборот вокруг оси?

100. Шайба массой 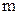скользит без трения с высоты по желобу, переходящему в вертикальную петлю радиуса 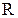. На какой высоте шайба оторвется от петли?

101. Гиря массой 10 кг падает с высоты 0,5 м на подставку, скрепленную с пружиной жесткостью . Определить сжатие пружины при ударе.

102. Пуля массой 15 г, летящая горизонтально со скоростью 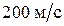, попадает в баллистический маятник длиной 1 м и массой 1,5 кг и застревает в нем. Определить угол отклонения маятника.

103. Подвешенный на нити шарик массой 200 г отклоняют на угол 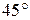. Определить силу натяжения нити в момент прохождения шариком положения равновесия.

104. Пренебрегая трением, определить наименьшую высоту , с которой должна скатываться тележка с человеком по желобу, переходящему в вертикальную петлю радиуса 6 м, и не оторваться от него в верхней точке петли.

105. Тонкий обруч скатывается без проскальзывания с наклонной плоскости высотой 2 м. Определить линейную скорость центра обруча в тот момент, когда он скатится с наклонной плоскости.

106. Точка участвует одновременно в двух взаимно перпендикулярных колебаниях, выражаемых уравнениями 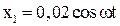и . Найти уравнение траектории точки и построить ее, указав направление движения.

107. Точка совершает одновременно два гармонических колебания одинаковой частоты, происходящих по взаимно перпендикулярным направлениям и выражаемых уравнениями: и . Найти уравнение траектории точки, построить ее с соблюдением масштаба и указать направление движения.

108. Точка совершает одновременно два гармонических колебания одинаковой частоты, происходящих по взаимно перпендикулярным направлениям и выражаемых уравнениями: 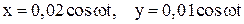. Найти уравнение траектории точки, построить ее с соблюдением масштаба и указать направление движения.

109. Точка совершает одновременно два гармонических колебания одинаковой частоты, происходящих по взаимно перпендикулярным направлениям и выражаемых уравнениями: 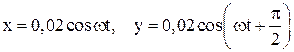. Найти уравнение траектории точки, построить ее с соблюдением масштаба и указать направление движения.

110. Точка совершает одновременно два гармонических колебания одинаковой частоты, происходящих по взаимно перпендикулярным направлениям и выражаемых уравнениями: 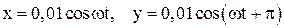. Найти уравнение траектории точки, построить ее с соблюдением масштаба и указать направление движения.

111. Точка совершает одновременно два гармонических колебания одинаковой частоты, происходящих по взаимно перпендикулярным направлениям и выражаемых уравнениями: . Найти уравнение траектории точки, построить ее с соблюдением масштаба и указать направление движения.

112. Точка совершает одновременно два гармонических колебания одинаковой частоты, происходящих по взаимно перпендикулярным направлениям и выражаемых уравнениями: . Найти уравнение траектории точки, построить ее с соблюдением масштаба и указать направление движения.

113. Точка совершает одновременно два гармонических колебания одинаковой частоты, происходящих по взаимно перпендикулярным направлениям и выражаемых уравнениями: 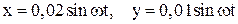. Найти уравнение траектории точки, построить ее с соблюдением масштаба и указать направление движения.

114. Точка совершает одновременно два гармонических колебания одинаковой частоты, происходящих по взаимно перпендикулярным направлениям и выражаемых уравнениями: 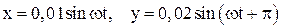. Найти уравнение траектории точки, построить ее с соблюдением масштаба и указать направление движения.

115. Два одинаково направленных колебания одного периода с амплитудами 10 и 6 см складываются в одно колебание с амплитудой 14 см. Найти разность фаз складываемых колебаний.

116. Определить амплитуду и начальную фазу результирующего колебания, возникающего при сложении двух колебаний и .

117. Точка участвует одновременно в двух гармонических колебаниях, происходящих по взаимно перпендикулярным направлениям и описываемых уравнениями: 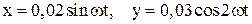. Соблюдая масштаб построить траекторию точки.

118. Точка участвует одновременно в двух гармонических колебаниях, происходящих по взаимно перпендикулярным направлениям и описываемых уравнениями: 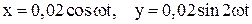. Соблюдая масштаб построить траекторию точки.

119. Точка участвует одновременно в двух гармонических колебаниях, происходящих по взаимно перпендикулярным направлениям и описываемых уравнениями: . Соблюдая масштаб построить траекторию точки.

120. Точка участвует одновременно в двух гармонических колебаниях, происходящих по взаимно перпендикулярным направлениям и описываемых уравнениями: . Соблюдая масштаб построить траекторию точки.

121. Два гармонических колебания, направленных по одной прямой и имеющие одинаковые амплитуды и периоды, складываются в одно колебание той же амплитуды. Найти разность фаз складываемых колебаний.

122. Точка участвует одновременно в двух гармонических колебаниях, происходящих по взаимно перпендикулярным направлениям и описываемых уравнениями: . Соблюдая масштаб построить траекторию точки.

123. Точка участвует одновременно в двух гармонических колебаниях, происходящих по взаимно перпендикулярным направлениям и описываемых уравнениями: . Соблюдая масштаб построить траекторию точки.

124. Точка участвует одновременно в двух гармонических колебаниях, происходящих по взаимно перпендикулярным направлениям и описываемых уравнениями: . Соблюдая масштаб построить траекторию точки.

125. Точка участвует одновременно в двух гармонических колебаниях, происходящих по взаимно перпендикулярным направлениям и описываемых уравнениями: . Соблюдая масштаб построить траекторию точки.

126. Амплитуда затухающих колебаний маятника за 5 мин уменьшилась в два раза. Во сколько раз уменьшится амплитуда колебаний за 15 мин?

127. Амплитуда затухающих колебаний маятника за 5 мин уменьшилась в два раза. За какое время, считая от начального момента, амплитуда уменьшится в восемь раз?

128. За 8 мин амплитуда затухающих колебаний маятника уменьшилась в три раза. Определить коэффициент затухания.

129. Во сколько раз уменьшится амплитуда колебания маятника за 8 мин, если коэффициент затухания 0,0023.

130. Амплитуда колебаний маятника длиной 1 м за 10 мин уменьшается в два раза. Определить логарифмический декремент затухания.

131. Во сколько раз уменьшится амплитуда колебаний маятника длиной 1 м за 10 мин, если логарифмический декремент затухания равен 0,0023.

132. Логарифмический декремент колебаний маятника равен 0,003. Определить число полных колебаний, которые должен сделать маятник, чтобы амплитуда уменьшилась в два раза?

133. Логарифмический декремент затухания колебаний маятника равен 0,003. Во сколько раз уменьшится амплитуда колебания через 231 полное колебание?

134. Тело массой 5 г совершает затухающие колебания. В течение какого времени тело потеряет 60% своей энергии, если коэффициент сопротивления 0,00009?

135. Тело массой 5 г совершает затухающие колебания. В течение 50 с тело потеряло 60% своей энергии. Определить коэффициент сопротивления.

136. На стержне длиной 30 см укреплены два одинаковых грузика: один в середине стержня, другой – на одном из концов. Стержень колеблется около горизонтальной оси, проходящей через свободный конец стержня. Определить период колебаний. Массой стержня можно пренебречь.

137. Однородный диск радиусом 20 см колеблется около горизонтальной оси, проходящей через одну из образующих цилиндрической поверхности диска. Каков период его колебаний.

138. Диск радиусом 24 см колеблется около горизонтальной оси, проходящей через середину одного из радиусов перпендикулярно плоскости диска. Определить период колебаний диска.

139. Тонкий прямой стержень длиной 130 см колеблется около горизонтальной оси, проходящей перпендикулярно стержню через точку, удаленную на некоторое расстояние от центра масс. При каком значении этого расстояния период колебаний имеет наименьшее значение?

140. Тонкий прямой стержень длиной 60 см колеблется около горизонтальной оси, проходящей перпендикулярно стержню, на некотором расстоянии от центра масс. Определить это расстояние, если период колебания равен 1,5 с.

141. К пружине подвесили груз, в результате чего пружина растянулась на 9 см. Каков будет период колебаний груза, если его немного оттянуть вниз и затем отпустить?

142. Математический маятник длиной 1 м установлен в лифте. Лифт поднимается с ускорением 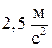. Определить период колебания маятника.

143. Диск радиусом 20 см колеблется около горизонтальной оси, проходящей перпендикулярно плоскости диска на расстоянии 15 см от центра масс. Определить период колебаний диска.

144. Тонкий обруч радиусом 0,5 м, подвешенный на гвоздь, вбитый горизонтально в стену, совершает малые колебания в плоскости параллельной стене. Определить период колебаний.

145. Стержень длиной 90 см совершает колебания около горизонтальной оси, проходящей перпендикулярно стержню на расстоянии 0,3 м от центра масс. Определить период колебаний стержня.

146. Какой объем занимает смесь газов, состоящая из 1 кг азота и 1 кг гелия при нормальных условиях?

147. В сосуде объемом 10 л содержится смесь газов, состоящая из 7 г азота и 1 г водорода при температуре 280 К. Определить давление смеси газов.

148. Найти плотность газовой смеси водорода и кислорода, если их массовые доли равны соответственно 0,11 и 0,89. Давление смеси равно 100 кПа, температура 300 К.

149. Газовая смесь, состоящая из кислорода и азота, находится в баллоне под давлением 1 Мпа. Определить парциальные давления кислорода и азота, если массовая доля кислорода в смеси равна 0,2.

150. Баллон объемом 30 л содержит смесь водорода и гелия при температуре 300 К и давлении 828 кПа. Масса смеси равна 24 г. Определить массу водорода и гелия.

151. В сосуде объемом 15 л находится смесь водорода и азота при температуре 300 К и давлении 200 кПа. Определить массу смеси и ее компонентов, если массовая доля азота в смеси равна 0,7.

152. Найти плотность газовой смеси водорода и кислорода, если их массовые доли равны соответственно 0,11 и 0,89. Давление смеси равно 100 кПа, температура 300 К.

153. Баллон объемом 5 л содержит смесь гелия и водорода при давлении 600 кПа. Масса смеси равна 4 г, массовая доля гелия равна 0,6. Определить температуру смеси.

154. Какой объем занимает смесь газов, состоящая из 1 кг азота и 1 кг гелия при нормальных условиях?

155. В сосуде объемом 10 л содержится смесь газов, состоящая из 7 г азота и 1 г водорода при температуре 280 К. Определить давление смеси газов.

156. Кислород, занимавший объем 1 л под давлением 1,2 Мпа, адиабатно расширился до объема 10 л. Определить работу расширения газа.

157. Азот массой 2 г, имевший температуру 300 К, был адиабатно сжат так, что его объем уменьшился в 10 раз. Определить конечную температуру и работу сжатия.

158. При адиабатном сжатии 1 кг кислорода совершена работа 100 кДж. Определить конечную температуру газа, если до сжатия кислород находился при температуре 300 К.

159. Какая работа совершается при изотермическом расширении 5 г водорода, взятого при температуре 290 К, если объем газа увеличился в три раза?

160. Определить работу адиабатного расширения 4 г водорода, если его температура понизилась на 10 К.

161. Газ, занимающий объем 12 л под давлением 100 кПА, был изобарно нагрет от 300 К до 400 К. Определить работу расширения газа.

162. Водород массой 4 г был нагрет на 10 К при постоянном давлении. Определить работу расширения газа.

163. Определить работу адиабатного расширения 4 г водорода, если его температура понизилась на 10 К.

164. Кислород, занимавший объем 1 л под давлением 1,2 Мпа, адиабатно расширился до объема 10 л. Определить работу расширения газа.

165. Азот массой 2 г, имевший температуру 300 К, был адиабатно сжат так, что его объем уменьшился в 10 раз. Определить конечную температуру и работу сжатия.

166. Расширяясь при постоянном давлении водород, совершил работу 6 кДж. Определить изменение внутренней энергии газа.

167. Расширяясь при постоянном давлении водород, совершил работу 6 кДж. Определить количество теплоты, сообщенное газу.

168. Азот массой 5 г был изохорно нагрет на 100 К. Определить: количество теплоты, сообщенное газу; работу газа; изменение внутренней энергии

169. При адиабатном расширении кислорода с начальной температурой 320 К внутренняя энергия уменьшилась на 8,4 кДж, а его объем увеличился в 10 раз. Определить массу кислорода.

170. Азот массой 200 г расширяется изотермически при температуре 280 К, причем объем газа увеличивается в три раза. Найти: изменение внутренней энергии газа; совершенную при расширении газа работу; количество теплоты, полученное газом.

171. Какая доля количества теплоты, подводимого к газу при изобарном процессе, расходуется на работу расширения газа. Рассмотреть случай трехатомного газа.

172. Какая доля количества теплоты, подводимого к газу при изобарном процессе, расходуется на увеличение внутренней энергии газа. Рассмотреть случай двухатомного газа.

173. Гелий массой 1 г был нагрет на 100 К при постоянном давлении. Определить: количество теплоты, сообщенное газу; изменение внутренней энергии; работу, совершенную газом.

174. Азот нагревался при постоянном давлении, причем ему было сообщено 21 кДж теплоты. Определить работу, которую совершил при этом газ, и изменение внутренней энергии.

175. Кислород при неизменном давлении 80 кПа нагревается так, что его объем увеличивается от 1 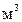до 3 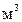. Определить: изменение внутренней энергии газа; работу, совершенную при расширении; количество теплоты, сообщенное газу.

176. На нагревание 160 г кислорода на 12 К было затрачено 1,76 кДж теплоты. Как протекал процесс: при постоянном давлении или при постоянном объеме?

177. Найти отношение для смеси газов, содержащей 8 г гелия и 2 г водорода.

178. Каковы удельные теплоемкости смеси газов, состоящей из 10 г аргона и 20 г азота?

179. Каковы удельные теплоемкости смеси газов, состоящей из 10 г водорода и 10 г углекислого газа?

180. На нагревание 160 г кислорода на 12 К было затрачено 1,76 кДж теплоты. Как протекал процесс: при постоянном давлении или при постоянном объеме?

181. Найти отношение для смеси газов, содержащей водород и неон, если массовые доли их одинаковы и равны 0,5.

182. Найти отношение для смеси газов, содержащей 10 г гелия и 4 г водорода.

183. Найти отношение для смеси газов, содержащей водород и неон, если массовые доли их одинаковы и равны 0,5.

184. Каковы удельные теплоемкости смеси газов, состоящей из 10 г аргона и 20 г азота?

185. Разность удельных теплоемкостей некоторого двухатомного газа равна 260 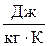. Найти молярную массу газа и его удельные теплоемкости.

Дата добавления: 2015-07-13