
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Про обозначения
|
|
|
|
К сожалению, обозначения логических операций И, ИЛИ и НЕ, принятые в «серьезной» математической логике (Ù, Ú,), неудобны, интуитивно непонятны и никак не проявляют аналогии с обычной алгеброй. Автор, к своему стыду, до сих пор иногда путает Ù и Ú. Поэтому на его уроках операция «НЕ» обозначается чертой сверху, «И» – знаком умножения (поскольку это все же логическое умножение), а «ИЛИ» – знаком «+» (логическое сложение).
В разных учебниках используют разные обозначения. К счастью, в начале задания ЕГЭ приводится расшифровка закорючек (Ù, Ú,), что еще раз подчеркивает проблему.
Что нужно знать:
· условные обозначения логических операций
A, 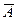 не A (отрицание, инверсия)
не A (отрицание, инверсия)
A Ù B, 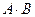 A и B (логическое умножение, конъюнкция)
A и B (логическое умножение, конъюнкция)
A Ú B, 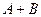 A или B (логическое сложение, дизъюнкция)
A или B (логическое сложение, дизъюнкция)
A → B импликация (следование)
· операцию «импликация» можно выразить через «ИЛИ» и «НЕ»:
A → B = A Ú B или в других обозначениях A → B = 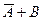
· если в выражении нет скобок, сначала выполняются все операции «НЕ», затем – «И», затем – «ИЛИ», и самая последняя – «импликация»
· правила преобразования логических выражений (слайд из презентации «Логика»):
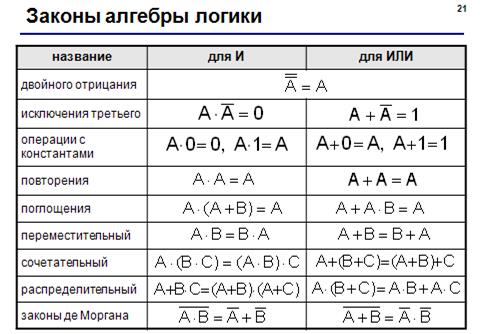
· фактически это задание на применение законов де Моргана (хотя об этом нигде не говорится):
(A Ù B) = A Ú B 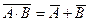
(A Ú B) = A Ù B 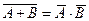
Пример задания:
Укажите, какое логическое выражение равносильно выражению A Ù (B Ú C).
1) A Ú B Ú C 2) A Ú B Ú C 3) A Ù B Ù C 4) A Ù B Ù C
Решение (вариант 1, использование законов де Моргана):
1) перепишем заданное выражение и ответы в других обозначениях:
заданное выражение 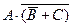
ответы: 1) 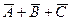 2)
2) 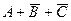 3)
3) 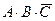 4)
4) 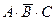
2) посмотрев на заданное выражение, видим инверсию (операцию «НЕ») для сложного выражения в скобках, которую раскрываем по формуле де Моргана,
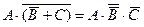
а затем используем закон двойного отрицания по которому 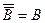 :
:
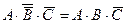
3) таким образом, правильный ответ – 3.
Возможные ловушки и проблемы:
· серьезные сложности представляет применяемая в заданиях ЕГЭ форма записи логических выражений с «закорючками», поэтому рекомендуется сначала внимательно перевести их в «удобоваримый» вид; при этом сразу становится понятно, что ответы 1 и 2 заведомо неверные
· при использовании законов де Моргана часто забывают, что нужно заменить «И» на «ИЛИ» и «ИЛИ» на «И» (возможный неверный ответ 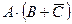 )
· расчет на то, что при использовании законов де Моргана инверсия сложного выражения по ошибке «просто пропадет», и все сведется к замене «ИЛИ» на «И» (неверный ответ )
· расчет на то, что при использовании законов де Моргана инверсия сложного выражения по ошибке «просто пропадет», и все сведется к замене «ИЛИ» на «И» (неверный ответ 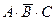 )
· иногда для решения нужно упростить не только исходное выражение, но и заданные ответы, если они содержат импликацию или инверсию сложных выражений )
· иногда для решения нужно упростить не только исходное выражение, но и заданные ответы, если они содержат импликацию или инверсию сложных выражений
|
Решение (вариант 2, через таблицы истинности, если забыли формулы де Моргана):
1) перепишем заданное выражение в других обозначениях:
заданное выражение 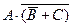
ответы: 1) 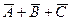 2)
2) 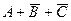 3)
3) 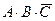 4)
4) 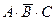
2) для доказательства равносильности двух логических выражений достаточно показать, что они принимают равные значения при всех возможных комбинациях исходных данных; поэтому можно составить таблицы истинности для исходного выражения и всех ответов и сравнить их
3) здесь 3 переменных, каждая из которых принимает два возможных значения (всего 8 вариантов, которые в таблице истинности записывают по возрастанию двоичных кодов – см. презентацию «Логика»)
4) исходное выражение 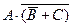 истинно только тогда, когда
истинно только тогда, когда 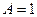 и
и 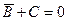 , то есть только при
, то есть только при  . (в таблице истинности одна единица, остальные – нули)
. (в таблице истинности одна единица, остальные – нули)
5) выражение 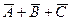 истинно, если хотя бы одна из переменных равна нулю, то есть, оно будет ложно только при
истинно, если хотя бы одна из переменных равна нулю, то есть, оно будет ложно только при 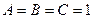 (в таблице истинности один нуль, остальные – единицы)
(в таблице истинности один нуль, остальные – единицы)
6) аналогично выражение 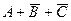 ложно только при
ложно только при 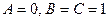 , а в остальных случаях – истинно
, а в остальных случаях – истинно
7) выражение 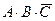 истинно только при
истинно только при 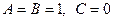 , а в остальных случаях – ложно
, а в остальных случаях – ложно
8) выражение 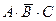 истинно только при
истинно только при 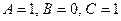 , а в остальных случаях – ложно
, а в остальных случаях – ложно
9) объединяя все эти результаты в таблицу, получаем:
| A | B | C | 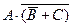
| 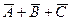
| 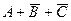
| 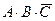
| 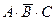
|
10) видим, что таблицы истинности исходного выражения и 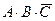 совпали во всех строчках
совпали во всех строчках
11) таким образом, правильный ответ – 3.
| Возможные проблемы: · сравнительно большой объем работы |
Выводы:
1) очевидно, что проще использовать первый вариант решения (упрощение исходного выражения и, если нужно, ответов), но для этого нужно помнить формулы
2) если формулы забыты, всегда есть простой (хотя и более трудоемкий) вариант решения через таблицы истинности.
Еще пример задания [1]:
Укажите, какое логическое выражение равносильно выражению
(A Ú B)Ú (A Ú B)Ú A Ù B
1) B Ù A 2) A Ù B Ú B 3) A Ù B Ú A 4) A
Решение (вариант 1, использование законов де Моргана):
1) перепишем заданное выражение в других обозначениях:
заданное выражение 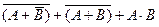
ответы: 1) 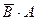 2)
2) 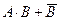 3)
3) 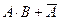 4)
4) 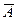
2) проще всего упростить заданное выражение; сначала раскрываем инверсию сложных выражений, используя законы де Моргана:
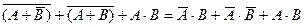
3) выносим за скобки 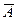 в первых двух слагаемых и используем закон исключения третьего
в первых двух слагаемых и используем закон исключения третьего 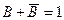 :
:
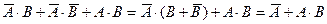
4) наконец, применяем распределительный закон для операции «И» и еще раз закон исключения третьего 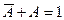 :
:
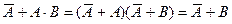
5) дальше уже не упрощается…
6) теперь замечаем, что такого ответа нет среди предложенных вариантов!
7) это означает, что ответы тоже можно упростить; упрощаем ответы 2 и 3, применяя распределительный закон и закон исключения третьего
ответы: 2) 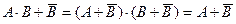
3) 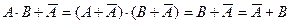
8) видим, что упрощенное выражение для ответа 3 совпало с упрощенным исходным выражением
9) таким образом, правильный ответ – 3
10) заметим, что этот пример можно также решать через таблицы истинности, но это более трудоемко.
Возможные проблемы:
· нужно хорошо помнить законы алгебры логики, которые не имеют аналога в математике (и «математическая» интуиция отказывает), но часто используются при упрощении логических выражений:
законы де Моргана: 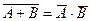 , , 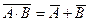 распределительный закон:
распределительный закон: 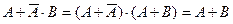 закон поглощения:
закон поглощения: 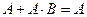 , , 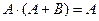 закон исключения третьего:
закон исключения третьего: 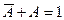 , , 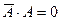
|
Задачи для тренировки [2]:
1) Укажите, какое логическое выражение равносильно выражению (A Ú B Ú C)?
1) A Ú B Ú C 2) A Ù B Ù C 3) A Ú B Ú C 4) A Ù B Ù C
2) Какое логическое выражение равносильно выражению (A Ù B) Ù C?
1) A Ú B Ú C 2) (A Ú B) Ù C 3) (A Ú B) Ù C 4) A Ù B Ù C
3) Укажите, какое логическое выражение равносильно выражению (А Ù B)?
1) A Ú B 2) A Ú B 3) B Ù A 4) A Ù B
4) Какое логическое выражение равносильно выражению (А Ú B)?
1) A Ú B 2) A Ù B 3) A Ú B 4) A Ù B
5) Какое логическое выражение эквивалентно выражению (A Ú B) Ù C?
1) (A Ú B) Ú C 2) A Ù B Ù C 3) (A → B)Ú C 4) (A Ú B)Ú C
6) Какое логическое выражение эквивалентно выражению A Ù (B Ù C)?
1) A Ù B Ù C 2) A Ú B Ú C 3) A Ù (B Ú C) 4) (A Ú B) Ù C
7) Какое логическое выражение эквивалентно выражению (A Ú B) Ù C?
1) (A Ú B) Ù C 2) (A Ù B) Ù C 3) (A Ù B) Ù C 4) (A Ú B) Ù C
8) Какое логическое выражение эквивалентно выражению (A Ú B) Ù C?
1) A Ú B Ù C 2) (A Ù B) Ù C 3) (A Ú C) Ú B 4) (A Ú C) Ù B
9) Какое логическое выражение эквивалентно выражению (A Ù B) Ù C?
1) (A Ù B) Ù C 2) (A Ú B) Ú C 3) (A Ù B) Ú C 4) (A Ú B) Ù C
10) Какое логическое выражение эквивалентно выражению (A Ú B) → C?
1) A Ù B Ù C 2) A Ú B Ú C 3) (A Ú B) Ú C 4) A Ú B Ú C
11) Какое логическое выражение эквивалентно выражению (A Ú B)Ù C?
1) A Ú B Ú C 2) (A Ú B)Ù C 3) (A Ú B)Ù C 4) A Ù B Ù C
12) Какое логическое выражение эквивалентно выражению A Ù (B Ú C)?
1) A Ù B Ù C 2) A Ú B Ú C 3) A Ù B Ù C 4) A Ú B Ú C
13) Какое логическое выражение эквивалентно выражению (A Ú B)Ù C?
1) A Ù B Ù C 2) (A Ù B) Ú C 3) (A Ù B) Ú C 4) A Ù B Ù C
14) Какое логическое выражение эквивалентно выражению (A Ù B Ù C)?
1) A Ú B Ú C 2) A Ú B Ú C 3) A Ù B Ù C 4) A Ù B Ù C
15) Какое логическое выражение эквивалентно выражению (A Ù B) Ù C?
1) A Ú B Ú C 2) A Ù B Ù C 3) (A Ú B) Ù C 4)(A Ù B) Ú C
16) Какое логическое выражение эквивалентно выражению (A Ù (B Ú C))?
1) A Ú B Ú C 2) A Ù B Ù C 3) A Ú B Ù C 4) A Ù B Ù C
17) Какое логическое выражение эквивалентно выражению (A Ú B Ù C)?
1) A Ù B Ù C 2) A Ù B Ú C 3) A Ù (B Ú C) 4) A Ù B Ú A Ù C
18) Какое логическое выражение эквивалентно выражению A Ù (B Ú C)Ú D?
1) A Ù B Ú C Ú D 2) A Ù B Ù C Ú D
3) A Ù B Ù C Ú D 4) A Ù B Ù C Ù D
19) Какое логическое выражение эквивалентно выражению (A Ú B)Ù C Ù D?
1) A Ù B Ù C Ù D 2) A Ú B Ù C Ù D
3) A Ú B Ú C Ú D 4) A Ù B Ù C Ù D
20) Какое логическое выражение эквивалентно выражению (B Ù C)Ù A?
1) A Ù (B Ù C) 2) A Ù B Ù C 3) A Ú B Ú C 4) A Ù (B Ú C)
21) Какое логическое выражение эквивалентно выражению A Ù(B Ú C)?
1) A Ù B Ù C 2) A Ù B Ú C Ù A 3) A Ù B Ú C 4) A Ù B Ú A Ù C
22) Какое логическое выражение эквивалентно выражению (A Ù B Ú C)?
1) A Ú B Ù C 2) A Ù B Ú C 3) A Ù (B Ú C) 4) A Ù C Ú B Ù C
23) Какое логическое выражение эквивалентно выражению (A Ú B Ú C)?
1) A Ù B Ù C 2) A Ù B Ù C 3) A Ú B Ú C 4) A Ú B Ú C
24) Какое логическое выражение эквивалентно выражению (A Ù B) Ú C?
1) A Ú B Ú C 2) A Ú B Ú C 3) A Ù B Ù C 4) A Ù B Ù C
25) Какое логическое выражение эквивалентно выражению A Ú (B Ú C)?
1) A Ú B Ú C 2) A Ú (B Ù C) 3) A Ú B Ú C 4) A Ú B Ú C
26) Какое логическое выражение эквивалентно выражению A Ú A Ù B?
1) A Ú B 2) A Ù B 3) A Ù B 4) A Ú B
27) Какое логическое выражение эквивалентно выражению (A Ú B) Ù (A Ú B)?
1) A Ú B 2) A 3) B 4) A Ù B
28) Какое логическое выражение эквивалентно выражению (A Ú B) Ù (A Ú B)?
1) A 2) A Ù B 3) A Ù B 4) B
29) Какое логическое выражение эквивалентно выражению A Ú B Ù A Ù B?
1) A 2) A Ù B 3) A Ù B 4) A Ú B
30) Какое логическое выражение эквивалентно выражению (A Ú B) Ù (A Ú B)?
1) A Ù B 2) A Ú B 3) A Ú B 4) A Ù B
31) Какое логическое выражение эквивалентно выражению A Ù B Ú (A Ú B)?
1) B Ù A 2) A Ù B 3) B Ù A 4) B Ù A
32) Какое логическое выражение эквивалентно выражению (A Ú B) Ú (A Ú B) Ú A Ù B?
1) B Ù A 2) A Ù B Ú B 3) A Ù B Ú A 4) A
33) Какое логическое выражение эквивалентно выражению (A Ù (B Ú C))?
1) A Ú B Ú C 2) A Ù B Ú C 3) A Ú B Ù C 4) A Ù B Ù C
34) Какое логическое выражение эквивалентно выражению A Ú ((A Ù B)) Ú C?
1) A Ú C 2) B Ú C 3) 1 4) 0
35) Какое логическое выражение эквивалентно выражению (A Ù B) Ú (B Ù C)?
1) A Ú B Ú C 2) A Ù B Ù C 3) A Ù B Ù C 4) A Ú B Ú C
36) Какое логическое выражение эквивалентно выражению (A Ú B) Ù (B Ú C)?
1) A Ú B Ú C 2) A Ù B Ù C 3) A Ù B Ù C 4) A Ù B Ù C
37) Какое логическое выражение эквивалентно выражению A Ú ((A Ù B)) Ú C?
1) A Ú C 2) 1 3) B Ú C 4) 0
[1] Самылкина Н.Н., Островская Е.М. Информатика: тренировочные задания. – М.: Эксмо, 2009.
[2] Источники заданий:
1. Демонстрационные варианты ЕГЭ 2004-2009 гг.
2. Гусева И.Ю. ЕГЭ. Информатика: раздаточный материал тренировочных тестов. — СПб: Тригон, 2009.
3. Самылкина Н.Н., Островская Е.М. Информатика: тренировочные задания. – М.: Эксмо, 2009-2010.
4. Якушкин П.А., Лещинер В.Р., Кириенко Д.П. ЕГЭ 2010. Информатика. Типовые тестовые задания. — М.: Экзамен, 2010.
5. Якушкин П.А., Ушаков Д.М. Самое полное издание типовых вариантов реальных заданий ЕГЭ 2010. Информатика. — М.: Астрель, 2009.
|
|
|
|
Дата добавления: 2015-07-13; Просмотров: 560; Нарушение авторских прав?; Мы поможем в написании вашей работы!