Функции принадлежности и методы их построения

Введенное определение нечеткого множества (2.1) не накладывает ограничений на выбор функции принадлежности. Однако, на практике целесообразно использовать аналитическое представление функции принадлежности μ A x нечеткого множества A с элементами x, нечетко обладающими определяющим множество свойством R. Типизация функций принадлежности в контексте решаемой технической задачи существенно упрощает соответствующие аналитические и численные расчеты при применении методов теории нечетких множеств. Выделяют следующие типовые функции принадлежности [32], [33].

Треугольные функции принадлежности, использующиеся для задания неопределенностей типа: «приблизительно равно», «среднее значение», «расположен в интервале», «подобен объекту», «похож на предмет» и т.п.:

· треугольная и трапецеидальная функции

trimf x,a,b,c = 0, x ≤ a; x - a b - a, a ≤ x ≤ b; c - x c - b, b ≤ x ≤ c; 0, c ≤ x; trapmf x,a,b,c,d = 0, x ≤ a; x - a b - a, a ≤ x ≤ b; 1, b ≤ x ≤ c; d - x d - c, c ≤ x≤ d; 0, d ≤ x;

Z-образные функции принадлежности, использующиеся для задания неопределенностей типа: «малое количество», «небольшое значение», «незначительная величина», «низкий уровень» и т.п.:

· квадратичный и гармонический Z-сплайны

zm f 1 x,a,b = 1, x ≤ a; 1 - 2 x - a b - a 2, a < x ≤ a + b 2; 2 b - x b - a 2, a + b 2 < x < b; 0, b ≤ x; zm f 2 x,a,b = 1, x < a; 1 2 + 1 2 cos x - a b - a; a ≤ x ≤ b; 0, x > b;

· Z-сигмоидальная и Z-линейная функции

sigmf x,a,b = 1 1 + exp - a x - b, a < 0; zlinemf x,c,d = 1, - ∞ < x ≤ c; d - x b - c, c < x ≤ d; 0, x > d;

S-образные функции принадлежности, использующиеся для задания неопределенностей типа: «большое количество», «большое значение», «значительная величина», «высокий уровень» и т.п.:

· квадратичный и гармонический S-сплайны

sm f 1 x,a,b = 0, x ≤ a; 2 x - a b - a 2, a < x ≤ a + b 2; 1 - 2 b - x b - a 2, a + b 2 < x < b; 1, b ≤ x; sm f 2 x,a,b = 0, x < a; 1 2 + 1 2 cos x - b b - a; a ≤ x ≤ b;1, x > b;

· S-сигмоидальная и S-линейная функции

sigmf x,a,b = 1 1 + exp - a x - b, a > 0; slinemf x,a,b = 0, x ≤ a; x - a b - a, a < x ≤ b; 1, x > b;

П-образные функции принадлежности, использующиеся для задания неопределенностей типа: «приблизительно в пределах от и до», «примерно равно», «около» и т.п.:

· колоколообразная и гауссова функции

gbellmf x,a,b,c = 1 1 + x - c a 2b; gaussmf x,σ,c = exp - x - c 2 2σ 2

Существует множество других функций принадлежности нечетких множеств, заданных как композиции вышеупомянутых базовых функций (двойная гауссова, двойная сигмоидальная и т.п.), либо как комбинации по участкам возрастания и убывания (сигмоидально-гауссова, сплайн-треугольная и т.п.).

Функция принадлежности μ A x – это некоторая не вероятностная субъективная мера нечеткости, определяемая в результате опроса экспертов о степени соответствия элемента x понятию, формализуемому нечетким множеством A. В отличие от вероятностной меры, которая является оценкой стохастической неопределенности, имеющей дело с неоднозначностью наступления некоторого события в различные моменты времени, нечеткая мера является численной оценкой лингвистической неопределенности, связанной с неоднозначностью и расплывчатостью категорий человеческого мышления. При построении функции принадлежности μ A x с каждым нечетким множеством A ассоциируется некоторое свойство, признак или атрибут R, который характеризует некоторую совокупность объектов X. Чем в большей степени конкретный объект x ∈ X обладает этим свойством R, тем более близко к соответствующее значение μ A x. Если элемент x ∈ X определенно обладает этим свойством R, то μ A x = 1, если же x ∈ X определенно не обладает этим свойством R, то μ A x = 0. Существуют прямые и косвенные методы построения функций принадлежности [18]-[20].

Прямые методы (наиболее известны методы относительных частот, параметрический, интервальный) целесообразно использовать для измеримых свойств, признаков и атрибутов, таких как скорость, время, температура, давление и т.п. При использовании прямых методов зачастую не требуется абсолютно точного поточечного задания μ A x. Как правило, бывает достаточно зафиксировать вид функции принадлежности и характерные точки, по которым дискретное представление функции принадлежности аппроксимируется непрерывным аналогом – наиболее подходящей типовой функцией принадлежности.

Косвенные методы (наиболее известен метод парных сравнений) используются в тех случаях, когда отсутствуют измеримые свойства объектов в рассматриваемой предметной области. В силу специфики рассматриваемых задач при построении нечетких систем автоматического управления, как правило, применяются прямые методы. В свою очередь, в зависимости от числа привлеченных к опросу экспертов как прямые, так и косвенные методы делятся на одиночные и групповые. Наиболее грубую оценку характеристических точек функции принадлежности можно получить путем опроса одного эксперта, который просто задает для каждого значения x ∈ X соответствующее значение μ A x.

Пример. Рассмотрим нечеткое множество A, соответствующее понятию «расход теплоносителя небольшой». Объект x – расход теплоносителя, X 0;x max – множество физически возможных значений скорости изменения температуры. Эксперту предъявляются различные значения расхода теплоносителя x и задается вопрос: с какой степенью уверенности 0 ≤ μ A x ≤ 1 эксперт считает, что данный расход теплоносителя x небольшой. При μ A x= 0 – эксперт абсолютно уверен, что расход теплоносителя x небольшой. Приμ A x = 1 – эксперт абсолютно уверен, что расход теплоносителя x нельзя классифицировать как небольшой.

Метод относительных частот. Пусть имеется m экспертов, n 1 из которых на вопрос о принадлежности элемента x ∈ X нечеткому множеству A отвечают положительно. Другая часть экспертов n 2 = m - n 1 отвечает на этот вопрос отрицательно. Тогда принимается μ A x = n 1 n 1 + n 2 = n 1 m.

Пример. Рассмотрим нечеткое множество A, соответствующее понятию «скорость изменения температуры положительная средняя». Объект x – скорость изменения температуры, X - x max; x max – множество физически возможных значений скорости изменения температуры. Экспертам предъявляются различные значения скорости изменения температуры x и каждому из них задается вопрос: считает ли эксперт, что данная скорость изменения температуры x положительная средняя. Результаты опроса сведены в табл.2.1.

Табл.2.1

Для непрерывного представления нечеткой переменной используем какую нибудь из П-образных функций принадлежности, например, Гауссову. Из множества гауссовых функций gaussmf x,σ,c = exp - x - c 2 2 σ 2 через характерные точки функции принадлежности: точку перехода μ A 3= 0,5 и максимумμ A 5= 1; проходит функция с параметрами σ = 1,7, c = 5. В качестве альтернативного метода перехода от дискретного ряда точек к непрерывному заданию функции принадлежности можно предложить поиск параметров Гауссовой функции принадлежности, максимально близко аппроксимирующей дискретный ряд по критерию СКО (рис.2.4).

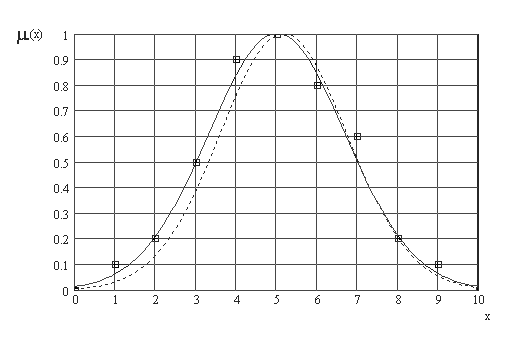
5.

1. Дополнение нечеткого множества 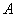обозначается символом 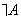(или иногда 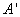) и определяется следующим образом:

(3.33)

Операция дополнения соответствует логическому отрицанию. Так, например, если 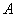— названиенечеткого множества, то «не 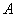» понимается как 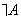(см. пример 3.8).

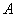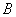2. Объединение нечетких множеств и обозначается (или, что более привычно, 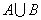) и определяется следующим образом:

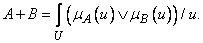(3.34)

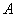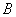Объединение соответствует логической связке «или». Так, если, например, и — названия нечетких множеств, то запись « 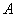или 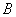» понимается как .

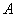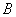3. Пересечение и обозначается 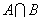и определяется следующим образом:

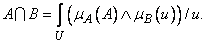(3.35)

Пересечение соответствует логической связке «и», т. е.

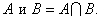(3.36)

Замечание 3.7. Следует иметь в виду, что

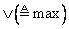и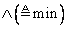

— не единственные операции, посредством которых можно определить операции объединения и пересечения (по этому вопросу см. [25] и [26]). В связи с этим важно отметить, что если операция «и» определяется с помощью операции min, как в (3.36), то она является «жесткой» в том смысле, что в ней недостаточно учитываются функции принадлежности обоих множеств. В противоположность этому операция «и», определяемая с помощью арифметического произведения, как в (3.37), является «мягкой». Какое из этих двух, а возможно, и других определений является наиболее подходящим, зависит от смысла, вкладываемого в эту операцию в каждом конкретном случае.

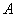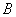4. Произведение и обозначается 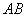и определяется формулой

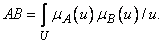(3.37)

Таким образом, любое нечеткое множество 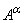, где 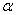— положительное число, следует понимать так:

(3.38)

Аналогично, если 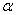— любое неотрицательное число, такое, ч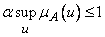то , то

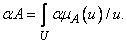(3.39)

Частными случаями операции возведения в степень [см. (3.35)] являются операция концентрирования, определяемая следующим образом

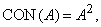(3.40)

и операция растяжения

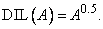(3.41)

Как будет показано в §6, операции концентрирования и растяжения полезны в представлении лингвистических неопределенностей.

Пример 3.8. Если

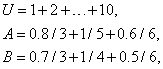(3.42)

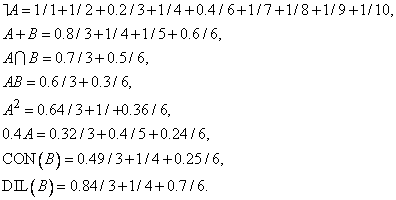(3.43)

5. Если 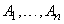— нечеткие подмножества универсального множества , а 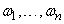— неотрицательные весовые коэффициенты, сумма которых равна 1, то выпуклой комбинацией нечетких множеств 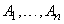называется нечеткое множество 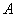с функцией принадлежности вида

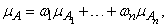(3.44)

где знак + означает арифметическое суммирование. Понятие выпуклой комбинации полезно в представлении таких лингвистических неопределенностей, как существенно, типично и т. п. [27].

6. Пусть 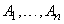— нечеткие подмножества универсальных множеств 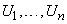соответственно. Декартово произведение этих подмножеств обозначается 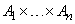и определяется как нечеткое подмножество множества 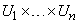с функцией принадлежности

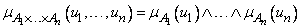. (3.45)

Таким образом [см. (3.52)],

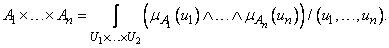(3.46)

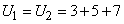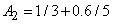Пример 3.9. Если , и , то

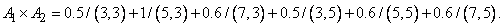(3.47)

7. Оператор увеличения нечеткости используется обычно для преобразования обычного (не нечеткого) множества в нечеткое или для увеличения нечеткости нечеткого множества. Так, результатом действия оператора увеличения нечеткости 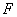на нечеткое подмножество 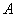множества является нечеткое подмножество 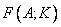вида

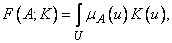(3.48)

где нечеткое множество 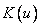является ядром оператора 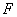, т. е. результатом действия оператора 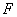на одноточечное множество :

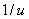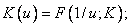(3.49)

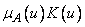— произведение (в смысле определения (3.39)) числа 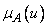и нечеткого множества 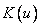, a 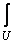— знак объединения семейства нечетких множеств 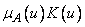, 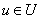. В сущности, выражение (3.48) аналогично интегральному представлению линейного оператора, в котором 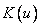играет роль импульсной переходной функции.

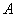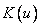Пример 3.10. Пусть , и определены следующий образом:

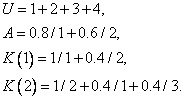(3.50)

Тогда

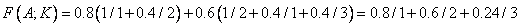(3.51)

Операция увеличения нечеткости играет важную роль в определении таких лингвистических неопределенностей, как более или менее, слегка, несколько (в какой-то степени), много и т. д. Например, если класс положительных чисел обозначить символом: 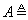положительный, тогда словосочетание слегка положительный является названием нечеткого подмножества множества действительных чисел, функция принадлежности которого имеет вид, показанный на рис. 3.1. В этом случае нечеткое понятие слегка есть оператор увеличения нечеткости, который преобразует нечеткое множество положительный в нечеткое множество слегка положительный. Однако не всегда возможно выразить результат действия оператора увеличения нечеткости в форме (3.48), причем оператор слегка как раз и представляет такой случай. Более подробное обсуждение этого и других вопросов, связанных с этим оператором, можно найти в [27].

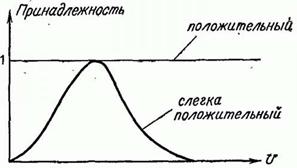
Рис. 3.1. Функции принадлежности значений положительный и слегка положительный

6. Основные свойства нечетких множеств

Пусть А, В, С - нечеткие множества, тогда выполняются следующие свойства:

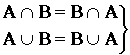- коммутативность;

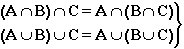- ассоциативность;

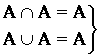- идемпотентность;

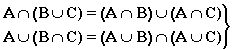- дистрибутивность;

A = A, где  - пустое множество, т.е. (x) = 0 >xE;

A = ;

AE = A, где E - универсальное множество;

AE = E;

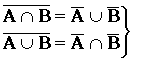- теоремы де Моргана.

В отличие от четких множеств, для нечетких множеств в общем случае:

A  ,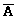

A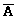  E.

(Что, в частности, проиллюстрировано выше в примере наглядного представления нечетких множеств).

Замечание. Введенные выше операции над нечеткими множествами основаны на использовании операций max и min. В теории нечетких множеств разрабатываются вопросы построения обобщенных, параметризованных операторов пересечения, объединения и дополнения, позволяющих учесть разнообразные смысловые оттенки соответствующих им связок " и ", " или ", " не ".

Один из подходов к операторам пересечения и объединения заключается в их определении в классе треугольных норм и конорм.

Треугольной нормой (t -нормой) называется двуместная действительная функция T:[0,1][0,1][0,1], удовлетворяющая следующим условиям:

T (0,0)=0; T ( _A, 1) = _A; T (1,  _A) = _A - ограниченность;

T(_A, _B) T(_C, _D), если _A_C, _B_D - монотонность;

T(_A,  _B) = T(_B, _A) - коммутативность;

T(_A, T( _B, _C))= T(T(_A, _B), _C) - ассоциативность;

Простым случаем треугольных норм являются:

min ( _A,  _B)

произведение _A_B

max (0, _A +  _B -1).

Треугольной конормой (t -конормой) называется двуместная действительная функция :[0,1][0,1] [0,1], со свойствами:

T (1,1) = 1; T(_A,0) =  _A; T (0,  _A) = _A - ограниченность;

T(_A, _B) T(_C, _D), если _A _C, _B _D - монотонность;

T(_A, _B) = T(_B, _A) - коммутативность;

T(_A, T(_B, _C)) = T(T(_A, _B), _C) - ассоциативность.

Примеры t -конорм:

max(_A,  _B)

_A + _B - _A _B

min(1, _A + _B).

Дата добавления: 2015-08-31