Алгебраические операции над нечеткими множествами 2 страница

Таким образом, задача обучения нейронной сети является задачей поиска минимума функции ошибки в пространстве состояний, и, следовательно, для ее решения могут применяться стандарные методы теории оптимизации. Эта задача относится к классу многофакторных задач, так, например, для однослойного персептрона с N входами и M выходами речь идет о поиске минимума в NxM-мерном пространстве.

На практике могут использоваться нейронные сети в состояниях с некоторым малым значением ошибки, не являющихся в точности минимумами функции ошибки. Другими словами, в качестве решения принимается некоторое состояние из окрестности обученного состояния W*. При этом допустимый уровень ошибки определяется особенностями конкретной прикладной задачи, а также приемлимым для пользователя объемом затрат на обучение.

Задача

Синаптические весовые коэффициенты однослойного персептрона с двумя входами и одним выходом могут принимать значения -1 или 1. Значение порога равно нулю. Рассмотреть задачу обучения такого персептрона логической функции “и”, как задачу многофакторной комбинаторной оптимизации. Для обучающей выборки использовать все комбинации двоичных входов.

26. Дельта-правило Собственно дельта-правилом называют математическую, несколько более общую форму записи правил Хебба. Пусть вектор {X}={x_1,x_2,...x_r,...x_m} — вектор входных сигналов, а вектор {D}={d_1,d_2,...d_k,...d_n} — вектор сигналов, которые должны быть получены от перцептрона под воздействием входного вектора. Здесь n — число нейронов, составляющих перцептрон. Входные сигналы, поступив на входы перцептрона, были взвешены и просуммированы, в результате чего получен вектор {Y}={y_1,y_2,...y_k,...y_n} выходных значений перцептрона. Тогда можно определить вектор ошибки ={e_1,e_2,...e_k,...e_n}, размерность которого совпадает размерностью вектором выходных сигналов. Компоненты вектора ошибок определяются как разность между ожидаемым и реальным значением выходного сигнала перцептронного нейрона:

{\Epsilon=D-Y}

При таких обозначениях формулу для корректировки j-го веса i-го нейрона можно записать следующим образом:

w_j(t+1)=w_j(t)+e_i x_j

Номер сигнала j изменяется в пределах от единицы до размерности входного вектора m. Номер нейрона i изменяется в пределах от единицы до количества нейронов n. Величина t — номер текущей итерации обучения. Таким образом, вес входного сигнала нейрона изменяется в сторону уменьшения ошибки пропорционально величине суммарной ошибки нейрона. Часто вводят коэффициент пропорциональности \eta, на который умножается величина ошибки. Этот коэффициент называют скоростью обучения. Таким образом, итоговая формула для корректировки весов:

w_j(t+1)=w_j(t)+\eta e_i x_j

27.

На приведенном рисунке использованы следующие условные обозначения:

• каждому слою нейронной сети соответствует своя буква, например: входному слою соответствует буква , а выходному – ;
• все нейроны каждого слоя пронумерованы арабскими цифрами;
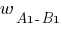• – синаптический вес между нейронам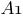и и ;
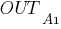• – выход нейрона .

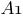В качестве активационной функции в многослойных персептронах, как правило, используется сигмоидальная активационная функция, в частности логистическая:

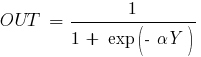
где 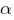– параметр наклона сигмоидальной функции. Изменяя этот параметр, можно построить функции с различной крутизной. Оговоримся, что для всех последующих рассуждений будет использоваться именно логистическая функция активации, представленная только, что формулой выше.

Сигмоид сужает диапазон изменения так, что значение лежит между нулем и единицей. Многослойные нейронные сети обладают большей представляющей мощностью, чем однослойные, только в случае присутствия нелинейности. Сжимающая функция обеспечивает требуемую нелинейность. В действительности имеется множество функций, которые могли бы быть использованы. Для алгоритма обратного распространения ошибки требуется лишь, чтобы функция была всюду дифференцируема. Сигмоид удовлетворяет этому требованию. Его дополнительное преимущество состоит в автоматическом контроле усиления. Для слабых сигналов (т.е. когда близко к нулю) кривая вход-выход имеет сильный наклон, дающий большое усиление. Когда величина сигнала становится больше, усиление падает. Таким образом, большие сигналы воспринимаются сетью без насыщения, а слабые сигналы проходят по сети без чрезмерного ослабления.

28.

Метод обратного распространения ошибки— метод обучения многослойного перцептрона. Впервые метод был описан в 1974 г. А.И. Галушкиным[1], а также независимо и одновременно Полом Дж. Вербосом[2]. Далее существенно развит в 1986 г. Дэвидом И. Румельхартом, Дж. Е. Хинтоном и Рональдом Дж. Вильямсом[3] и независимо и одновременно С.И. Барцевым и В.А. Охониным (Красноярская группа)[4].. Это итеративный градиентный алгоритм, который используется с целью минимизации ошибки работы многослойного перцептрона и получения желаемого выхода.

Основная идея этого метода состоит в распространении сигналов ошибки от выходов сети к её входам, в направлении, обратном прямому распространению сигналов в обычном режиме работы. Барцев и Охонин предложили сразу общий метод («принцип двойственности»), приложимый к более широкому классу систем, включая системы с запаздыванием, распределённые системы, и т. п.[5]

Для возможности применения метода обратного распространения ошибки передаточная функция нейронов должна быть дифференцируема. Метод является модификацией классического метода градиентного спуска.

29.

Проблемы обучения нейронных сетей

Хотя основной алгоритм обучения многослойных нейронных сетей (BPM) открыт уже достаточно давно и весьма хорошо исследован, обучение нейронных сетей в данный момент по-прежнему больше напоминает шаманство, нежели технологию. Исследователи вынуждены пробовать множество разнообразных архитектур сетей, обучать каждую из них в отдельности и затем выбирать ту, которая наилучшим образом решает поставленную задачу Разумеется, существуют общие рекомендации по выбору архитектуры сети для решения определенного класса задач, существует также известная формула для грубой оценки количества элементов скрытого слоя по количеству необходимого числа синаптических весов в многослойной сети с сигмоидальными передаточными функциями размерность входного сигнала, размерность выходного сигналачисло элементов обучающей выборки

Получив необходимое число весов, можно рассчитать число нейронов в скрытых слоях. Например, если речь идет о двухслойной сети, число нейронов в скрытом слое будет

Однако это еще не решает проблемы, так как после задания архитектуры нейронной сети ее все равно необходимо обучать. По своей сути нейронная сеть является универсальным аппроксиматором. Это означает, что в процессе настройки она не вычисляет целевую функцию, а как бы лишь подбирает внутренний набор функций, при сложении которых образуется функция, выдающая на выходе ряд значений, напоминающий исходный ряд, предъявленный ей в процессе обучения (аппроксимационный полином). Отсюда следует вывод, что выходные данные работающей нейронной сети всегда будут содержать ошибку, причем величина этой ошибки никогда заранее не известна. Известно только, что в процессе обучения данная ошибка, возможно, будет уменьшена до некоторого приемлемого уровня. Рабочая точка нейросетевой системы в процессе обучения скользит по поверхности ошибок по направлению к глобальному минимуму целевой функции. Причем, в силу неровности рельефа поверхности ошибок, сеть может застрять в локальном минимуме очень далеко от ожидаемого глобального. Если склон локального минимума достаточно крут, а шаг обучения слишком мал, чтобы рабочая точка выкатилась на его край, наступает состояние, называемое параличом сети, при котором сеть на обучающей выборке дает недостаточно точные результаты, а обучение при этом все равно останавливается Существует также состояние, когда ошибка обучения начинает беспорядочно колебаться (осциллировать) и сеть входит в состояние переобучения (рис. 4). Это соответствует слишком точной аппроксимации обучающих данных

Состояние переобучения: 1; истинная зависимость; 2 слишком точная аппроксимация полиномом

Также имеются трудности, связанные с внутренней организацией входных данных Это так называемое проклятие размерности В общем случае входные данные содержат шум и некоторое количество малозначащей информации. При попытке заставить сеть разобрать все это по кластерам без предварительной подготовки входных данных мы рискуем получить неверные обобщения. С другой стороны, если внутренняя структура данных нам неизвестна (задача кластеризации в чистом виде), мы в подобной ситуации вынуждены увеличивать число входных элементов сети. Необходимое число входных нейронов быстро возрастает с увеличением размерности кластеризуемого пространства (приблизительно как 2 Nа вслед за увеличением числа входных нейронов неизбежно изменяется и число нейронов скрытого слоя, иначе процесс кластеризации может сопровождаться потерями значимой информации. Это усложняет процесс обучения нейронной сети и делает его менее предсказуемым

30.

Различия вычислительных процессов в сетях часто обусловлены способом взаимосвязи нейронов, поэтому выделяют следующие виды сетей:

Сети прямого распространения – сигнал проходит по сети от входа к выходу в одном направлении;

Сети с обратными связями;

Сети с боковыми обратными связями;

Гибридные сети;

В целом, по струтуре связей ИНС могут быть сгруппированы в два класса: сети прямого распространения – без обратных связей в струтуре и рекуррентные сети – с обратными связями.

31.

Нейронные сети Кохонена — класс нейронных сетей, основным элементом которых является слой Кохонена. Слой Кохонена состоит из адаптивных линейных сумматоров («линейных формальных нейронов»). Как правило, выходные сигналы слоя Кохонена обрабатываются по правилу «Победитель получает всё»: наибольший сигнал превращается в единичный, остальные обращаются в ноль.

По способам настройки входных весов сумматоров и по решаемым задачам различают много разновидностей сетей Кохонена. Наиболее известные из них:

сети векторного квантования сигналов, тесно связанные с простейшим базовым алгоритмом кластерного анализа (метод динамических ядер или K-средних);

самоорганизующиеся карты Кохонена;

сети векторного квантования, обучаемые с учителем

Самоорганизующаяся карта состоит из компонентов, называемых узлами или нейронами. Их количество задаётся аналитиком. Каждый из узлов описывается двумя векторами. Первый — т. н. вектор веса m, имеющий такую же размерность, что и входные данные. Второй — вектор r, представляющий собой координаты узла на карте. Карта Кохонена визуально отображается с помощью ячеек прямоугольной или шестиугольной формы; последняя применяется чаще, поскольку в этом случае расстояния между центрами смежных ячеек одинаковы, что повышает корректность визуализации карты.

Изначально известна размерность входных данных, по ней некоторым образом строится первоначальный вариант карты. В процессе обучения векторы веса узлов приближаются к входным данным. Для каждого наблюдения (семпла) выбирается наиболее похожий по вектору веса узел, и значение его вектора веса приближается к наблюдению. Также к наблюдению приближаются векторы веса нескольких узлов, расположенных рядом, таким образом если в множестве входных данных два наблюдения были схожи, на карте им будут соответствовать близкие узлы. Циклический процесс обучения, перебирающий входные данные, заканчивается по достижении картой допустимой (заранее заданной аналитиком) погрешности, или по совершении заданного количества итераций. Таким образом, в результате обучения карта Кохонена классифицирует входные данные на кластеры и визуально отображает многомерные входные данные в двумерной плоскости, распределяя векторы близких признаков в соседние ячейки и раскрашивая их в зависимости от анализируемых параметров нейронов.

В результате работы алгоритма получаются следующие карты:

карта входов нейронов — визуализирует внутреннюю структуру входных данных путем подстройки весов нейронов карты. Обычно используется несколько карт входов, каждая из которых отображает один из них и раскрашивается в зависимости от веса нейрона. На одной из карт определенным цветом обозначают область, в которую включаются приблизительно одинаковые входы для анализируемых примеров.

карта выходов нейронов — визуализирует модель взаимного расположения входных примеров. Очерченные области на карте представляют собой кластеры, состоящие из нейронов со схожими значениями выходов.

специальные карты — это карта кластеров, полученных в результате применения алгоритма самоорганизующейся карты Кохонена, а также другие карты, которые их характеризуют

32.

Самоорганизу́ющаяся ка́рта Ко́хонена— нейронная сеть с обучением без учителя, выполняющая задачу визуализации и кластеризации. Идея сети предложена финским учёным Т. Кохоненом. Является методом проецирования многомерного пространства в пространство с более низкой размерностью (чаще всего, двумерное), применяется также для решения задач моделирования, прогнозирования и др. Является одной из версий нейронных сетей Кохонена.

Самоорганизующиеся карты Кохонена используются для решения таких задач, как моделирование, прогнозирование, выявление наборов независимых признаков, сжатие информации, а также для поиска закономерностей в больших массивах данных. Наиболее часто описываемый алгоритм применяется для кластеризации данных

33.

Нейро́нная сеть Хо́пфилда — полносвязная нейронная сеть с симметричной матрицей связей. В процессе работы динамика таких сетей сходится (конвергирует) к одному из положений равновесия. Эти положения равновесия являются локальными минимумами функционала, называемого энергией сети (в простейшем случае — локальными минимумами отрицательно определённой квадратичной формы на n-мерном кубе). Такая сеть может быть использована как автоассоциативная память, как фильтр, а также для решения некоторых задач оптимизации. В отличие от многих нейронных сетей, работающих до получения ответа через определённое количество тактов, сети Хопфилда работают до достижения равновесия, когда следующее состояние сети в точности равно предыдущему: начальное состояние является входным образом, а при равновесии получают выходной образ

34.

Исследование известных архитектур гибридных систем и алгоритмов их обучения позволяет, по нашему мнению, считать их моделями, адекватно отражающими соотношение восприятия и логического умозаключения при когнитивной деятельности человека. При реальном решении задачи, человек комбинирует процессы мышления (компьютерный аналог – логический вывод), вспоминания (сознательное «внутреннее» возбуждение образа), восприятия окружающих предметов (распознавание) и, возможно, движения (управление телом). Обученная нечеткая нейронная сеть и хранит паттерны, и выполняет логические операции, так как содержит И-ИЛИ- нейроны, и переключается от распознавания на логический вывод, так как обычно включает в себя несколько отдельно обученных сетей с разными функциями.

Таким образом, несмотря на то, что нечеткие нейронные сети созданы как нейро-нечеткие контроллеры для управления процессами, они могут служить когнитивной моделью для изучения взаимодействия процессов восприятия и мышления при когнитивной деятельности.

Следующей особенностью гибридных систем является их принципиальная интерпретируемость, то есть как и всякая система логического вывода гибридная система объясняет свой результат с помощью обратного просмотра протокола применяемых вербализованных правил. Любая нечеткая нейронная сеть работает как система нечеткого логического вывода, но строится не с помощью инженерии знаний, а с помощью обучения по образцам. В результате матрица весов отражает силу связи входных и выходных переменных. Результатом обучения нечеткой нейронной сети служит не только матрица весов, но совокупность правил и оценок их достоверности. Следовательно, любая гибридная система является как минимум двухуровневой системой, включающей систему и метасистему, отражающую систему первого уровня. Исходя из сказанного, можно предложить нечеткие нейронные сети в качестве когнитивной модели соотношения сознательного (логического) и бессознательного (аналогового, вычислительного) процессов в решении интеллектуальной задачи.

Таким образом, в нечеткой нейронной сети возможно сочетать манипулирование образами, заданными количественными параметрами, с преобразованием символов (слов). Такая возможность заложена в самой базовой конструкции теории нечетких множеств. Каждое нечеткое множество связывает слово, имя с порядковой или метрической шкалой с помощью функции принадлежности, т.е. количественно моделирует новое качество – смысл.

Для всех классов нейронных сетей, в том числе гибридных систем, связь системы с окружением устанавливается с помощью обучающей выборки. Чем более полна и адекватна обучающая выборка, тем выше аппроксимирующая или классифицирующая способность нейронной сети после обучения. При использовании кроме классического метода обратного распространения сигнала, еще и генетического алгоритма обучения, гибридные системы получают еще один инструмент адаптации – функцию оптимальности генетического алгоритма, fitness-function.

35.

Следовательно, для обучения искусственной нейронной сети необходимо учитывать большое количество параметров и накопительный объем информации. Это приведет к усложнению построения модели.

Устранить данный недостаток можно за счет построения нейронечетких систем, которые относятся к классу гибридных систем, в основе которых лежат нечеткая логика, нейронные сети и генетический алгоритм [7].

Рассмотрим класс адаптивных сетей функционально эквивалентных системам нечетких рассуждений. Подобная архитектура носит название ANFIS (Adaptive Neuro-Fuzzy Inference System – адаптивная нейронечеткая система заключений) [5, 8].

Нейронечеткая система имеет пять слоев (рис. 1) и описывается следующим способом:

1. Выходы узлов первого слоя представляют собой значения функций принадлежности при конкретных значениях входных параметров:

,

где x – входной сигнал узла i, Ai – лингвистическая переменная, связанная с данной узловой функцией, (x) – функция принадлежности переменной Ai, определяющей степень, с которой данный x удовлетворяет Ai.

Параметры, значения которых будут подаваться на входы нейронов первого слоя х1, х2, х3, х4. Каждый параметр может иметь несколько определяющих значений отнесения по отдельным входам.

2. Выходами нейронов второго слоя являются степени истинности предпосылок каждого правила базы знаний системы.

,3

3. Каждый i-ый узел третьего слоя определяет отношение веса i-го правила к сумме весов всех правил:

4. Нейроны четвертого слоя выполняют операции вычисления значений для функций принадлежностей выходного параметра. Для модели типа Сугено:

где fi – функции принадлежности выходных переменных.

5. Единственный узел данного слоя является фиксированным узлом, в котором вычисляется полное выходное значение адаптивной сети как сумма всех входных сигналов

.

Дата добавления: 2015-08-31