Вибір перешкодостійкого коду і розробка пристроїв захисту від помилок

У каналах з перешкодами ефективним засобом підвищення врогідності передачі повідомлень є перешкодостійке кодування. Воно засноване на застосуванні спеціальних кодів, які коректують помилки, викликані дією перешкод. Код називається коректуючим, якщо він дозволяє виявляти або виявляти і виправляти помилки при прийомі повідомлень. Для того, щоб код володів коректуючими здібностями, в кодовій послідовності повинні міститися додаткові (надмірні) символи, призначені для коректування помилок.

Коректуюча здатність коду залежить від кодової відстані d, яка чисельно дорівнює мінімальному числу елементів, якими відрізняється кодова комбінація від будь-якої іншої. У загальному випадку:

d = t0+ti+1;

(5.1)

де t₀ та t_i - число виявлених і виправлених помилок відповідно.

Якщо код тільки виявляє помилки, то

d = t0+1;

(5.2)

а у випадку тільки виправлення

d = 2 ti+1.

(5.3)

Основними характеристиками коду (крім кодової відстані) є його потужність і коефіцієнт надмірності.

Потужність коду N_p – число комбінацій (кодових слів) із загального числа 2ⁿ, використовуваних в даному коді для передачі повідомлень (такі комбінації називають робочими)

Np = 2^m.

(5.4)

Комбінації, що не входять до числа робочих, використовуються для перевірки правильності приходу закодованої комбінації: якщо прийнята комбінація не належить до робочих, то це означає, що в процесі передачі відбулася помилка.

Кількість перевірочних елементів k коректуючого кода залежить від виду кода.

Коефіцієнтом надлишковост кода називають відношення

kн = k / n.

(5.5)

Чим більше надмірність коду, тим вище його коректуюча здатність. Код, за допомогою якого тільки виявляються помилки, носить назву виявляючого коду. Виправлення помилки при такому кодуванні зазвичай проводиться шляхом повторення спотворених повідомлень. Запит про повторення передається по каналу зворотного зв'язку. Код, який виправляє виявлені помилки, називається виправляючим кодом. В цьому випадку фіксується не тільки сам факт наявності помилок, але і встановлюється, які кодові символи прийняті помилково, що дозволяє їх виправити без повторної передачі. Відомі також коди, в яких виправляється тільки частина виявлених помилок, а решта помилкових комбінацій передається повторно.

В курсовому проекті пропонується використовувати один з наступних видів перешкодостійких кодів:

- код з контролем парності;

- код з повторенням і інверсією;

- ітеративний код;

- код Хеммінга;

- циклічний код.

При побудові коду із контролем парності в кожній комбінації двійкового коду вводиться додатковий розряд, щодоповнює кількість одиниць в комбінації до парного числа. Потужність такого коду N_p = 2 ^n-1, коефіцієнт надлишковості k_н = 1/n. Приймальний пристрій в цьому випадку бракує всі комбінації, які містять непарне число одиниць, що дозволяє виявляти всі помилки непарної кратності. Підрахунок числа одиниць в кодовій комбінації доцільно виконувати підсумовуванням по модулю 2 її елементів, або за допомогою спеціальних елементів контролю парності [4, 7, 9]. Аналогічно будується код із захистом по непарності.

Код з повторенням і інверсією будується таким чином: кожна комбінація двійкового коду залежно від числа одиниць в ній або просто повторюється, або повторюється з інвертуванням. Потужність такого коду N_p = 2 ^n/2, коефіцієнт надлишковості k_н = 0,5. Приймальний пристрій повинен спочатку проаналізувати першу половину кодової комбінації і у разі парного числа одиниць в ній порівняти її з другою половиною, з якою вона повинна співпасти. У разі ж непарного числа одиниць в першій половині вона інвертується і після цього перевіряється на збіг з другою половиною. У загальному випадку код з повторенням і інверсією може використовуватися не тільки для виявлення, але і для виправлення всіх одноразових помилок [7, 9].

Ітеративний код характеризується наявністю двох або більше системи перевірок всередині кожної кодової комбінації [4, 5, 7]. Будується він таким чином (див. рис. 5.1): одна або декілька кодових комбінацій групуються у вигляді матриці || q_ij || розмірністю i ´ j, де i – число рядків, а j – число стовпців. В кінці кожного рядка додається перевірочний розряд r_i, який дорівнює сумі по модулю 2 всіх елементів рядка; крім того вводиться додатковий рядок, елементи якого s_j дорівнюють сумі по модулю 2 елементів j-го стовпця (елемент s_j+1 дорівнює сумі по модулю 2 перевірочних розрядів r_i).

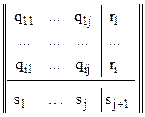
Рис. 5.1 – Формування матриці ітеративного коду

При використанні ітеративного коду в курсовому проекті доцільно складати кодову матрицю для кожного опитуваного об'єкту, в цьому випадку в кожному рядку можна помістити кодове слово, що несе інформацію від одного з датчиків. Тоді кількість стовпців буде дорівнювати кількості інформаційних розрядів m, а кількість рядків – кількості датчиків на кожному опитуваному об'єкті. Потужність такого коду N_p = (2ⁱ)^j, кількість перевірочних розрядів – k = i + j + 1.

На приймальні стороні перевірка правильності приходу кодової комбінації здійснюється підсумовуванням по модулю 2 елементів кожного рядка і кожного стовпця з урахуванням контрольних розрядів. При правильному прийомі всі суми повинні дорівнювати нулю. Цей код має кодову відстань d = 4 і дозволяє виявляти всі помилки кратності до трьох і непарної кратності. Основним недоліком ітеративного коду являється його відносно висока надмірність.

Код Хеммінга – один з найбільш ефективних кодів, що дозвляють виявляти і виправляти одиночні помилки [4-7, 9]. Кодова відстань d=3. Код утворюється шляхом доповнення інформаційної частини передаваного блоку, що складається з m біт, k перевірочними елементами, причому в інформаційну частину при кодуванні можна включати і службові символи (номер, початок і кінець блоку), за винятком маркерних комбінацій, які доцільно розташовувати на початку блоку.

При визначенні кількості перевірочних елементів k слід керуватися нерівністю

2^k ³ k + m + 1.

(5.6)

Оскільки m визначене, то не важко підібрати найменше число k, що задовольняє умові (5.6).

Код будується так, щоб в результаті k = n – m перевірок отримати k-розрядне двійкове число, що вказує номер спотвореної позиції кодової комбінації. Для цього перевірочні символи повинні знаходитися на позиціях, номери яких виражаються степенем числа 2 (2⁰, 2¹, 2², …, 2^k-1), оскільки кожен з них входить тільки в одне з перевірочних рівнянь. Таким чином, якщо нумерувати позиції зліва направо, то контрольні символи повинні знаходитися на першій, другій, четвертій, восьмій і так далі позиціях.

Перевірочні елементи коду Хеммінга утворюються шляхом підсумовування по модулю 2 певних розрядів безнадмірної кодової комбінації. Результат першої перевірки дає цифру молодшого розряду синдрому помилки в двійковому записі, отже, першою перевіркою повинні бути охоплені символи з номерами, що містять в двійковому записі одиниці в першому розряді (1, 3, 5, 7 і так далі). результат другої перевірки дає цифру другого розряду синдрому помилки, отже, другою перевіркою повинні бути охоплені символи з номерами, що містять в двійковому записі одиниці в другому розряді (2, 3, 6, 7, 10 і так далі). Аналогічно при i-ій перевірці повинні перевірятися символи, номери яких в двійковому записі містять одиниці в i-ому розряді. Таким чином, перевірочні групи повинні мати вигляд:

k1 = q1 Å q 3 Å q 5 Å q 7 Å q 9 Å …; k2 = q2 Å q 3 Å q 6 Å q 7 Å q10 Å …; k3 = q4 Å q 5 Å q 6 Å q 7 Å q12 Å …; k4 = q8 Å q 9 Å q10 Å q11 Å q12 Å ….

(5.7)

При декодуванні здійснюється підсумовування по модулю 2 правої і лівої частин кожного рівняння з (5.7). Результат підсумовування покаже синдром помилки. Якщо всі розряди синдрому дорівнюють нулю, то помилок не виявлено, інакше синдром указуватиме номер розряду, в якому відбулася помилка.

Циклічні коди знаходять найбільше розповсюдження в системах передачі даних з вирішальним зворотним зв'язком, що обумовлене їх високими коректуючими властивостями, порівняно простою реалізацією, невисокою надлишковістю. Особливо вони ефективні при виявленні пакетів помилок. Циклічні коди відносяться до блоково-систематичних кодів, в яких кожна комбінація кодується самостійно у вигляді блоку таким чином, що інформаційні і перевірочні елементи завжди знаходяться на певних місцях [4-7, 9]. Для спрощення процедури кодування і декодування перевірочні біти розміщують в кінці блоку. Кодування передаваного повідомлення здійснюється множенням двійкової послідовності G(x) на одночлен x^k, що має ту ж степінь, що і створюючий поліном P(x), з додаванням до цього добутку залишку R(x), отриманого після ділення добутку G(x)×x^k на створюючий поліном, тобто передаване в канал зв'язку повідомлення F(x) має вигляд:

F(x) = G(x)x^k Å R(x).

(5.8)

При декодуванні послідовність F(x), що приймається, знову ділиться на створюючий поліном P(x). Отриманий нульовий залишок R(x) = 0 свідчить про відсутність помилок в прийнятому блоці, а відмінність залишку від нуля – про наявність помилок. Аналізуючи залишок можна визначити номери спотворених розрядів і скоректувати їх.

Для побудови циклічних кодів в якості створюючих поліномів використовуються многочлени, що не приводяться, тобто многочлени, які без залишку діляться тільки на себе і на одиницю. Поліном P(x) може бути представлений у алгебраїчній формі або у вигляді двійкового або вісімкового числа. У останньому випадку кожна вісімкова цифра відображає три двійкові розряди. Наприклад, для полінома P(x) = x⁵ + x² + 1 двійковий запис має вигляд 100101, а відповідний йому вісімковий – 43. У таблиці 5.1 приведені всі многочлени, що не приводяться, до п'ятої степені, а в [2, 4] – вибіркові многочлени, що не приводяться, до дев'ятої степені, а також їх двійкові і вісімкові еквіваленти.

При виборі створюючого полінома P(x) слід мати на увазі, що степінь створюючого полінома не може бути менше числа перевірочних елементів k. Для спрощення технічної реалізації кодерів і декодерів необхідно обирати степінь полінома рівну k. Якщо в таблиці є декілька многочленів, що не приводяться, даної степені, то доцільно вибрати найкоротший, причому число ненульових членів P(x) не повинне бути менше необхідної кодової відстані, визначеної по (5.1).

До всякого коду обов'язково пред'являється вимога однозначності декодування. У разі блокових кодів це означає, що всякій послідовності або групі послідовностей кодових символів повинна однозначно відповідати послідовність елементів передаваного повідомлення, що завжди виконується при використанні рівномірних кодів.

Таблиця 5.1 – Многочлени, що не приводяться, і їх еквіваленти

Степінь поліному	Поліном P(x)	Двійковий еквівалент	Вісімковий еквівалент
	x + 1
	x^2 + x + 1
	x^3 + x + 1
	x^3 + x^2 + 1
	x^4 + x + 1
	x^4 + x^3 + 1
	x^4 + x^3 + x^2 + x + 1
	x^5 + x^2 + 1
	x^5 + x^3 + 1
	x^5 + x^3 + x^2 + x + 1
	x^5 + x^4 + x^2 + x + 1
	x^5 + x^4 + x^3 + x + 1
	x^5 + x^4 + x^3 + x^2 + 1

Використовувані в даний час способи кодування не дозволяють наблизитися до теоретичної пропускної спроможності реальних каналів зв'язку при достатньо малій ймовірності помилки (високій вірності прийому). Для цього знадобилися б дуже складні, економічно не вигідні схеми кодування і декодування. Проте за допомогою розумно вибраного коду часто вдається значно підвищити швидкість передачі або вірність прийому.

Питання реалізації схемотехніки кодерів і декодерів описаних вище перешкодостійких кодів досить детально представлені в [2, 4-7].

Дата добавления: 2015-08-31